Intuitive and Holistic Aerodynamics
The practical men did not like “scientific” aerodynamics.50 So what sort of aerodynamics did they like? I begin to answer this question by identifying what might be called their “practical epistemology.” Then I look in more detail at the accounts of lift that are to be found in books written for the designers of airplanes and in articles that appeared in the Aeroplane, Flight, and Aeronautics.
The epistemology of the practical man was intuitive and qualitative. It was formulated in conscious opposition to the pedantic concern with accuracy and irrelevant detail attributed to the despised figure of the mathematician.51 Reality must be grasped in all its complexity rather than simplified and broken down into imagined elements. In this sense their epistemology was holistic. It was also artistic. A good designer could rely on his eye, his experience, and his judgment. In a literature review in Aeronautics the editor said: “I don’t deny the infinitely valuable role of pure science, still less that of theory, but science should have some relation to practice, since it is its foster-mother. There is more than one aeroplane designer who knows just enough mathematics to make twice two work out at four, but he will turn out machines equal in performance to the best. We in this country know, as they do in the United States, of eminent designers who see a new type of machine rather than design it.”52
Grey made the point more bluntly with no genuflection in the direction of science: “Never mind what the scientists calculate. Trust the man who guesses, and guesses right.”53 The claim was that some designers have a track record of guessing rightly, and these are the people to trust. We may not be able to see how they do it, but we should not let this put us off. Trust rather than understanding lies at the root of things. This was indeed Grey’s view: there were not only unknown factors involved in the design of aircraft but there were actually unknowable factors, and this was something the “slide – rule scientists” could not grasp.54
The implication was that the reasons behind practical success will remain mysterious. This notion implied a species of intellectual pessimism or even nihilism. Such pessimism was not unusual among practical men and was sometimes echoed by those in the other camp. For example, writing as J. C., a reviewer of G. P. Thomson’s Applied Aerodynamics recommended the book to practical designers (even though it was the product of Farnborough) and said, “One of the first ideas that arises in the reading is the state of ignorance that still exists in aerodynamics; it is safe to say that we know practically nothing of the reasons for the experimental results that we find. The amazing thing is that we are able to make aeroplanes as well as we can.”55
At least two of these statements come from spokesmen of the practical men rather than from designers themselves, but they seem to articulate a widely held view. Grey’s characteristic denunciations were repeated in a foreword he wrote in 1917 for the book Aeroplane Design by F. S. Barnwell, who was the chief designer at the British and Colonial Aeroplane Company. This firm, usually known as the Bristol Company, became famous during the Great War for the Bristol fighter, which was designed by Barnwell.56 Much harm had been done, said Grey, “both to the development of aeroplanes and to the good repute of genuine aeroplane designers by people who pose as ‘aeronautical experts’ on the strength of being able to turn out strings of incomprehensible calculations resulting from empirical formulae based on debatable figures acquired from inconclusive experiments carried out by persons of doubtful reliability on instruments of problematic accuracy.”57 If one asks what is left when all the hated calculations, experiments, and instruments have been swept away, the answer is intuition. This was Grey speaking, not Barnwell, so we cannot be sure that Barnwell endorsed it. Authors do not necessarily agree with what others say in the forewords of their books, but it is reasonable to expect general agreement.
W. H. Sayers, a strong critic of the National Physical Laboratory, was involved with the development of seaplanes during World War I. In an article written after the war, in 1922, called “The Arrest of Aerodynamic Development,” Sayers described the current conception and form of the airplane.58 It was, he said, “the hybrid product of two utterly different and independent methods of development.” From 1908 to 1914, its evolution was “the result almost entirely of individual adventure.” There were, he insisted, no wind – tunnel results worth mentioning, the mathematics of stability had no apparent connection with the facts, and even engineers regarded the airplane as a mechanical curiosity. “Individual designers worked, as artists worked, by a sort of inspiration as to what an aeroplane ought to be like, and built as nearly to their inspiration as the limited means, appliances and increasing knowledge they possessed would allow them” (138). Sayers went on to deplore the degree of standardization that had set in with regard to design. This, he said, gave a spurious sense of understanding and control. In reality we did not know how to predict what would happen outside the limited range with which we had become familiar. Similarly, the laboratory workers had been in error in concentrating on simple bodies, especially “such simple bodies as might be used as components of the standard type of aeroplane” (138). The result, he said, was a bias toward an additive conception of the different aspects of design and a tendency to overlook large, qualitative effects such as the interference of different components.
Like many other practical men, Sayers was skeptical about model work.59 In his view, aerodynamicists did not yet know what dynamic “similarity” really was, so that inferences from models remained doubtful. Full-scale experimentation was the real basis of knowledge. Grey could be relied upon to give the relatively measured prose of Sayers, his frequent contributor, a more colorful rendering: “I would back any one of a dozen men I know to find out more about streamlines in a month at Brooklands, with the help of a borrowed racing car, a jobbing carpenter, and a spring-balance, than the combined efforts of the National Physical Laboratory, Chalais-Meuden, the Eiffel Tower, the laboratory at Kouchino, and the University of Gottingen have discovered since flying first attracted the attention of that section of humanity which the Americans expressively call ‘the high-brow.’”60
This cavalier dismissal of all the major aerodynamic laboratories of Europe dramatizes the anti-intellectual strand in the epistemology. Not all of its expressions were so markedly of this character, but there is no denying a tendency in this direction. Nor can one deny a certain justice in the stance. If scientists have a tendency to simplify the complex and decompose it into its elements, where does this leave the designer who has to reassemble the elements in novel ways? Even if simple principles can be discovered, it can still be unclear how these principles interact when they work together. Design is still a matter of judgment about their combination and compromise in their balance.
Grey’s dismissive attitude toward Gustav Eiffel’s work was not shared by all practical men. The impression created by articles and reviews in the technical journals is that Eiffel was seen as an engineer who could be relied upon to operate in a practical way. If Eiffel’s large, empirical monograph, replete with tables of data, graphs and diagrams of airplanes, is laid side by side with
Greenhill’s mathematical report, there can be no more striking visual proof of the extremes of style that can be represented in aeronautical work. What is more, Eiffel’s work was frequently compared favorably with the experimental work of the NPL. Where the two laboratories diverged, the practical men backed Eiffel.
The reviewer of Eiffel’s La resistance de Fair et Faviation, for the Aero, in March 1911, was enthusiastic: “One is hardly going too far in describing this book as the most authoritative work on the subject that has yet appeared, and it is especially valuable in as much as the experiments have been evolved with an eye specially inclined toward their value in practical aeronautics. . . while experiments of a more purely academic interest have. . . been relegated to the background.” This, the reviewer continued, was strikingly different from the situation that “obtains in more than one experimental laboratory.”61
Writing in July 1916, the editor of Aeronautics invited readers to compare Eiffel, “working almost single handed,” with the National Physical Laboratory: “It would not be unjust to say that Eiffel attains practical results, neglecting a slight margin of error, accounting probably 2 per cent. in extreme cases, which for the time being and for practical purposes is inappreciable. On the other hand, the N. P.L., in its beautiful work, seems rather to strive for the meticulous elimination of this negligible margin of error and passes by the major facts.” Ask Eiffel for the air resistance of, say, an airship hull and the job is done “in a couple of days,” while it would last “heaven knows how many weeks” at the N. P.L.62
The report of the Advisory Committee for 1911-12 noted that, between Eiffel’s laboratory and the NPL, there were differences of some 15 percent between the values of the lift coefficient for certain wings. The probable reason, it was said, was observational errors. The ACA resolved to investigate the matter and to ensure that a high degree of accuracy was maintained at Teddington. The “Editorial View” in the Aero was that to the “lay mind” such differences are “disquieting,” and the writer of the editorial chose to read the ACA’s response “almost as an acknowledgement of error on the part of Teddington.”63











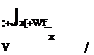 w = Ь£а
w = Ь£а