Lanchester’s Treatise

Frederick William Lanchester (fig. 4.7) was born in 1868, the son of an archi­tect.10 He was educated at the Royal College of Science and Finsbury Techni­cal College. He began work in 1889 with a company making gas engines, and in 1895 he began to develop his own motorcar. Until 1919 he was managing director and then the consultant engineer of the Lanchester Motor Company Ltd. He was responsible for some important patents for devices that suc­cessfully reduced the vibration that plagued early engines. During this time Lanchester had also been working on the problems of artificial flight and experimenting with model gliders. In 1907 he assembled the ideas about lift that he had been developing since the mid-1890s and published them in the form of a bulky volume called Aerodynamics, the first of a two-volume Trea­tise on Aerial Flight.11 This work is now recognized as the locus classicus of the circulation theory of lift, though it does not read like a modern textbook on aerodynamics. The circulation theory is only one strand in the argument that had evolved over some dozen years and had been changed to bring it more into line with the concepts used in, for example, Lamb’s Hydrodynamics.12 The precise character of the changes and the form in which the theory was

first conceived are not known, though they may, to some extent, be guessed from the variations in the uneven text.

Aerodynamics shows the traces of at least five interwoven lines of argu­ment: (1) an evolutionary perspective, (2) the concept of a wing being carried on a wavelike airflow, (3) a quasi-Newtonian idea of the “sweep” of a wing, (4) examples of the theory of discontinuous flow, and (5) versions of the theory of circulation or the vortex theory. Although Lanchester devoted all of chapter 3 of his book to an exposition of basic hydrodynamic ideas, the assimilation was incomplete. He did not avail himself of the mathematical formula expressing the circulation as an integral, though he did accept the ideas behind it. Furthermore, his use of the word “circulation” was not con­sistent. It was often used informally to refer to fluid that was displaced by a body and pushed from the front to the rear.13 Tracking the word “circula­tion” in Lanchester’s text does not necessarily reveal those places where the circulation theory of lift was being developed. Terminologically, Lanchester preferred to speak of “cyclic flow.”

The theoretical centerpiece of the 1907 book was chapter 4, called “Wing Form and Motion in the Periptery.” The word “periptery” was coined by Lanchester to refer to the characteristic form of airflow in the vicinity of a lift­ing surface. The chapter began with an evolutionary argument and a criticism of an existing theory of lift. In order to perform its biological function, argued Lanchester, the wing of a bird must have evolved into a shape that conforms to the pattern of airflow necessary to provide lift. It should therefore be pos­sible to read off this pattern of flow from the shape of the wing. All such natu­rally occurring wings show a similar “design and construction” that involves an arched profile and a slight downward inclination of the front edge. From this Lanchester inferred that the air must be moving upward as it approaches the leading edge of the wing and downward as it leaves the trailing edge.

The advantages of the dipping front edge was first recognized by Horatio Phillips, who made it the subject of two patents in 1884 and 1891, but, said Lanchester, Phillips gave an incorrect account of it. According to Phillips the air impinged on the sloping, upper surface of the leading edge and was deflected upward, off the surface of the wing, leaving a partial vacuum on the upper surface. Lanchester rejected this in favor of an explanation based on principles drawn from Newton’s mechanics. The central point, he said, was the exchange of momentum. The air, which was rising at the front of the wing, had to have the vertical component of its motion reduced to zero. The air then had to be given a downward direction, and thus supplied with another vertical component of motion, but this time in the opposite direc­tion. It was important, said Lanchester, that during this process the flow of air remained conformable to the shape of the wing and that no surfaces of discontinuity were created.

These ideas were developed by means of a thought experiment involv­ing the fall of a flat plate. The plate was to fall so that it presented its full surface-area to the direction of its descent. During the fall the air would be pushed around the edges from the lower to the upper surface. “There is at first a circulation of air round the edge of the plane from the under to the upper surface, forming a kind of vortex fringe” (145). (Notice that here the word “circulation” refers to the air being literally displaced from the front to the back of the object.) Lanchester then supposed the falling plate was given a horizontal velocity. This, he said, made the case equivalent to an inclined plane moving horizontally. If, following Newton, air is treated as if it is made up of independent particles, the analysis gives the wrong answers. Lanchester concluded that it was necessary to take account of the continuous nature of the fluid medium but knew of no way to do this for the flow under consid­eration. This led him to introduce a (more or less) arbitrary “sweep” factor to define the amount of air that was involved in the momentum exchange. It was Lanchester’s references to “sweep,” rather than circulation, that were picked up by the practical men.

Lanchester then explored a number of different approaches. The reader was told that “the peripteroid system may be regarded as a fixed wave” (156), though this idea was nowhere adequately explained. It seems to have been part of an early version of the theory. A few pages later Lanchester explained that because the disturbances in the neighborhood of the aerofoil possess an­gular momentum, it can be inferred that the flow comprises a cyclic motion. Lanchester went on: “The problem, then, from the hydrodynamic stand­point, resolves itself into the study of cyclic motion superposed on a transla­tion” (162). He then used the formulas of mathematical hydrodynamics to plot the streamlines and potential lines for the flow around a circular cylinder on the assumption that the flow contained a circulation or cyclic component. Graphical methods were used to establish that the imbalance of pressures furnished a lift force. The flow depicted in the plot did not look like a picture of the flow round a wing, because there was a circular cylinder, rather than a winglike profile, at the center of the action, but, said Lanchester, we may look upon this figure “as representing in section a theoretical wing-form, or aerofoil, appropriate to an inviscid fluid” (163). He justified this statement by observing that from “the hydrodynamic standpoint,” that is, with a perfect fluid, the shape of the aerofoil section is irrelevant.

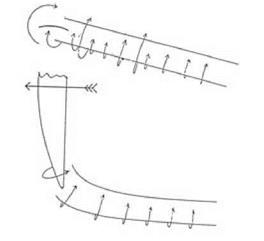
Lanchester then moved from perfect fluids to real fluids and from the in­finite wing to the wing of finite length where the behavior of the air at the tips had to be considered. Finite wings could be understood by supposing that the cyclic flow extends beyond the wingtips in the form of two vortices issuing from the ends of the wing and trailing behind it. The trailing vortices could be assumed to extend back to the point on the ground from which the aircraft took off. Such a picture meets the requirement, first identified by Helmholtz, that a vortex can only end on a surface of the fluid. Lanchester acknowledged that, because of Kelvin’s theorem, the creation of such vortices in a perfect fluid presented a problem. He argued that viscosity had to be invoked to start the process, but inviscid theory could be used for the subsequent description. He also noted that the two trailing vortices would interact with one another. As Lanchester put it, “We have seen. . . that the lateral terminations of the aerofoil give rise to vortex cylinders. . . . Such a supposition presents no dif­ficulties in a viscous fluid. . . . Now we know that two parallel vortices, such as we have here, possessed of opposite rotation. . . will precess downwards as fast as they are formed” (173). Lanchester then referred his readers to the diagram that is reproduced here as figure 4.8.

Lanchester now had a qualitative account of lift that fulfilled the following conditions: (1) it was based on “cyclic” flow, that is, a flow around a vortex with circulation; (2) it was applicable to a finite wing; (3) it identified the role of trailing vortices; and (4) it made appeal to the viscosity of air as well as to conceptions derived from ideal fluid theory.14