Glauert’s Textbook
In the German-speaking world the circulation theory of lift and Prandtl’s wing theory found their way into the textbooks during the Great War. Richard Grammel, who taught mechanics at the technische Hochschule in Danzig, led the way in 1917 with his Die hydrodynamischen Grundlagen des Fluges5 In 1919, immediately after the war, Arthur Proll of the TH in Hannover, published Flugtechnik: Grundlagen des Kunstfluges.52 H. G. Bader published his Grundlagen der Flugtechnik in 1920, and in 1922 Richard Fuchs of Berlin and Ludwig Hopf of Aachen produced their comprehensive Aerodynamik.53 The content and level of these books contrasted markedly with what was available on the British textbook scene. As described earlier, both Cowley and Levy’s Aeronautics in Theory and Experiment of 1918 and Bairstow’s Applied Aerodynamics of 1920 dismissed the circulatory theory, whereas G. P. Thomson’s Applied Aerodynamics of 1919 was almost purely empirical. Thomson spoke of the “complete failure” (26) of mathematical hydrodynamics to account for lift. He concluded that an account of lift required an understanding of eddies and turbulent motion: “This is the solution we want for aerodynamics, and not that found by the ordinary mathematical method” (32). In 1926 the situation changed radically when Cambridge University Press published Hermann
Glauert’s Elements of Aerofoil and Airscrew Theory.54 This work showed the power of the “ordinary mathematical method” of which Thomson, like most of his Cambridge companions, had despaired. Glauert’s Elements proved to be an outstanding work of exposition which, even today, some eighty years later, is still confidently recommended to students.55
The book consisted of seventeen brief chapters and surveyed all the main themes of modern aerofoil theory for a reader with no previous knowledge of fluid mechanics (though a significant degree of mathematical competence was presupposed). The first chapter described the main facts to be explained, while chapters 2-5 outlined the theory of perfect fluids. Chapters 6 and 7 introduced the theory of conformal transformation and the specific properties of the Joukowsky transformation. Chapter 8 dealt with viscosity and drag. Here Glauert introduced the Stokes equation for viscous flow and informally derived Prandtl’s boundary-layer approximation. Chapter 9 was called “The Basis of Aerofoil Theory,” and in it Glauert sought to bring together the apparently antithetical ideas of viscous and inviscid flow into a practical synthesis. His aim was “to obtain the true conception of a perfect fluid” (127). The form of the desired synthesis was described by Glauert as follows: “The viscosity must be retained in the equations of motion and the flow of a perfect fluid must be obtained by making the viscosity indefinitely small” (117).
When analyzing the motion of an object in a fluid, the concept of a perfect fluid must be deployed in a way that retains the effects of viscosity. If a perfect fluid is defined as a fluid devoid of viscosity, such a requirement is contradictory: how can the viscosity, which is excluded by definition, also be “retained”? Here, once again, Glauert sought to convey his novel, Gottin – gen-style methodology. He argued that the requirement he formulated can be satisfied even though the boundary conditions, the way the fluid behaves at a solid boundary, are wholly different for a perfect fluid and for a viscous fluid. (For a perfect fluid the boundary conditions are that it cannot penetrate the solid boundary but it can slide smoothly along it; for a viscous fluid the conditions are zero penetration of the boundary and zero slip along it.) The trick needed to retain viscosity in the equations of motion is to start with a viscous boundary layer of finite thickness around the object and imagine it to become an infinitely thin sheet of vorticity. The boundary layer is a real phenomenon belonging to viscous fluids, and a vortex sheet is an idealization appropriate to perfect fluids. The connecting link that allows viscosity to be “retained” is that
in the limit the boundary layer becomes a vortex sheet surrounding the surface of the body and the vortices of this sheet act as roller bearings between
the surface of the body and the genera! mass of the fluid. The conception of a perfect fluid with a vortex sheet surrounding the surface of the body therefore represents the limiting conditions of a viscous fluid when the viscosity tends to zero, and the existence of the vortex sheet implies that the perfect fluid solution need not satisfy the condition of zero slip at the boundary. (117-18)
If the cross section of a wing is drawn in two dimensions, the line that traces its profile is to be thought of as made up of an infinite number of points acting like infinitesimal roller bearings. These rollers are said to be rotating fluid elements, that is, “fluid elements in vortical motion” (119), and they stand in for the boundary layer. The rotating fluid elements pass along the surface of the body and finally leave it to pass downstream in the wake. Glauert linked this picture to von Karman’s work on the so-called vortex street that exists behind a bluff body placed in a fluid flow. Clearly Glauert was introducing a significant degree of idealization, but even this degree would soon be surpassed. Having replaced the boundary layer on the wing surface by a sheet of vorticity, the chord and profile of the wing was then ignored altogether. In two dimensions the wing was reduced to a single point, that is, to the “cross section” of a line of vorticity imagined to be perpendicular to the page on which the figure is drawn.
How did Glauert explain the origin of the circulation around a wing? The discussion of this sensitive and difficult question was located in a short section of chapter 9. Combining candor with British understatement, Glauert introduced the issue as follows: “The process by which the circulation round an aerofoil develops as the aerofoil starts from rest presents certain theoretical difficulties, since the process would be impossible in a perfect fluid, and it is again necessary to consider the limiting condition as the viscosity tends to zero” (121). Circulation is impossible if the analysis starts with p = 0 and confines itself to this condition. To overcome the difficulty it is necessary to start by considering p Ф 0 and then make the transition from viscous to nonviscous flow by imagining that p ^ 0. Here within the one sentence we see the British and German conceptions of an ideal fluid directly juxtaposed. Glauert then proceeded to offer a qualitative account of the required transition. The analysis effectively hinged on two diagrams of the flow at the trailing edge of a wing. I reproduce the diagrams in figure 9.11.
At low speeds, as the aerofoil starts from rest, the air behaves like an ideal fluid and curves round the trailing edge as shown in (a) in figure 9.11. There is a stagnation point S on the upper surface not far from the trailing edge. Glauert argued that, as the velocity increases, the streamlines coming from the undersurface are unable to turn round the trailing edge “owing to the large viscous forces brought into action by the high velocity gradient” (121).
|
figure 9.11. The initial moment in the creation of a vortex (a). The vortex detaches itself from the trailing edge and floats downstream (b), leaving behind an opposing circulatory tendency. From Glauert 1926, 121. (By permission of Cambridge University Press) |
The flow thus breaks away from the trailing edge in the manner shown in (b). The result is that “a vortex is formed between the trailing edge and the old stagnation point S” (121). When the vortex has reached a certain stage of development, it breaks away and floats downstream in the wake of the wing.
Although Glauert does not make the point explicitly, it is obviously important for the argument that the vortex that detaches itself and moves downstream is rotating in the correct direction. Its direction of rotation determines the direction of the circulation in any contour that surrounds it. The information about the direction in which the vortex rotates is contained in Glau – ert’s diagram rather than his text. The diagram shows that the vortex rotates in a counterclockwise direction. Why counterclockwise? The presumption must be that the flow that initially went round the trailing edge and then progressively failed to navigate the sharp corner is moving more rapidly than the flow that comes away from the stagnation point. The speed difference of the adjacent bodies of fluid would constitute a surface of discontinuity and hence a surface of vorticity—and the differences, in this case, would produce a counterclockwise vortex.
The next step in the argument was equally crucial. In the diagram a vortex has detached itself from the wing, and this, the argument goes, generates an equal and opposite circulation around the wing. The detached vortex had a counterclockwise circulation, so the circulation around the wing will be clockwise, and this produces the speed differential postulated by the circulation theory. But why does this process create an equal and opposite circulation? The answer given by Prandtl and Glauert was that such an outcome is required in order that Kelvin’s theorem is satisfied. Kelvin’s theorem initially looked as if it would rule out the onset of circulation entirely. If there is zero circulation at the onset of movement, there will be zero circulation at all later times. But the enemy is now converted into an ally. Glauert explained that the circulation around a large contour, enclosing both the wing and the detached vortex, will indeed stay zero. This is necessary to satisfy Kelvin’s theorem, but the theorem can be satisfied by virtue of two opposing vortices whose
|
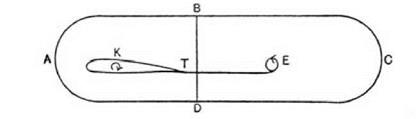
figure 9.12. The creation of circulation around a wing (around contour ABD) counterbalances the circulation (around the contour BCD) created by the vortex which detaches itself from the trailing edge. The two opposing circulations sum to zero, and thus the flow is said to conform to Kelvin’s theorem. Kelvin’s theorem entails that if there is no circulation in the flow of an ideal fluid when motion begins, then there can be no circulation at a later time. From Glauert 1926, 121. (By permission of Cambridge University Press) |
respective circulations cancel each other out. The argument is represented diagrammatically in figure 9.12, again taken from Glauert. The large contour is called ABCD. The vortex is called E, and the circulation around the wing is K, while the circulation around the vortex is, accordingly, -K. As Glauert put it: “the circulation round any large contour ABCD which surrounded the aerofoil initially was and must remain zero, and as this contour includes the vortex E there must be a circulation K round the aerofoil which is exactly equal and opposite to the circulation round the vortex E” (121). The detached vortex floats away on the free stream with velocity V, leaving the wing with circulation K and lift given by the Kutta-Joukowsky law L = pKV. Glauert’s argument was moving rapidly at this point, but though potentially puzzling, this sequence of steps is now to be found in all standard textbooks.
Having prepared the ground in the first nine chapters, Glauert moved on to discuss the aerofoil in three dimensions. In chapter 10 he introduced the mathematics of the simple and refined horseshoe vortex system as well as the important concepts of induced velocity and induced drag. In chapters 11-13 he dealt with the effects of varying the aspect ratio of a wing and generalized the results to biplanes. In chapter 14 he discussed wind-tunnel corrections, while in the final chapters, 15 and 16, he applied the circulation theory to the airscrew.