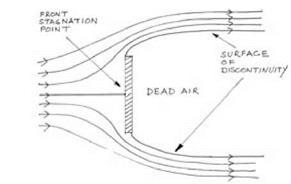
Surfaces of Discontinuity

Consider the idealized model of the postcard experiment, that is, the stream­lines around a flat plate normal to the flow. The flow could take the form shown in figure 2.7 as well as that already shown in figure 2.5. Instead of curl­ing around the edges of the plate and moving down the back of the plate, the flow of ideal fluid can break away at the edges. Behind the plate the flow is not a mirror image of the flow in front of it but consists of a body of “dead air,” or dead fluid, bounded by the moving fluid which has met the plate, moved along the front face of the plate, and separated at the edges. The pressure in the “dead air” will be the same as that at a great distance from the plate and can be equated with the atmospheric pressure. In a real, viscous fluid, the moving fluid and the dead or stationary fluid would interact. There would be a transition layer, with a speed gradient created by the stationary fluid retarding the moving fluid while the moving fluid sought to drag the station­ary fluid along with it. In an ideal fluid there will be no such transition layer because there will be no traction between the two bodies of fluid. The free

stream will pass smoothly over the dead fluid so there will be a sudden transi­tion from fluid with zero velocity to fluid with a nonzero velocity. Mathema­ticians call this sudden transition a discontinuity in the velocity because there are no intermediate values. This term gives rise to the general label for flows of this kind, which are called discontinuous flows. The streamline that marks the mathematically sharp discontinuity between the moving and stationary bodies of fluid is called a free streamline. It is a line of intense vorticity along which the flow possesses rotation in the technical sense defined earlier in the chapter.

This attempt to make mathematical hydrodynamics more realistic was introduced by Helmholtz in 1868 in a paper titled “Uber discontinuirliche Flussigkeits-Bewegungen” (On discontinuous fluid motions).40 Helmholtz argued that all the flows that had produced d’Alembert’s paradox had de­pended not only on the assumption that the flow was inviscid but also on the assumption that the velocity distribution was continuous. Helmholtz explored flows involving surfaces of separation (Trennungsflache) or (what is mathematically equivalent) sheets of vorticity (Wirbelflache).41 Of course, said Helmholtz,

Die Existenz solcher Wirbelfaden ist fur eine ideale nicht reibende Flussigkeit eine mathematische Fiction, welche die Integration erleichtert. (220-21)

The existence of such a vortex sheet for an ideal inviscid fluid is a mathemati­cal fiction to make the integration [of the equations] easier.

But fiction or no fiction, Helmholtz had raised the hope that the glaringly false consequences of the standard picture of ideal-fluid flow could be avoided.

If a steady, discontinuous flow is to be possible, certain conditions must be satisfied. It must be the case that the static pressure on either side of the free streamline is the same, otherwise the flow pattern would not be in equi­librium and would modify itself. Since the flow at a great distance in front of the plate is assumed to have a constant speed V and to be at atmospheric pressure pa, while the dead air is also at atmospheric pressure, then the speed of the flow along the free streamlines that bound the dead air must also be V. This conclusion follows from Bernoulli’s equation relating speed and pres­sure. Bernoulli’s law also leads to the conclusion that a flow of this kind will generate a greater pressure on the front of the plate than on the back.

Consider the streamline that terminates at the stagnation point at the front of the plate. What is the pressure on the front of the plate at the stagna­tion point? Call the pressure p. Everywhere along the streamline that goes to the stagnation point, the static and dynamic pressure will sum to the same constant value, that of the Bernoulli constant or the total pressure head. The value of the constant, or the total pressure, at a distance from the plate is H = pa+ Уг p V2. On the plate, at the stagnation point, the speed is zero. There will be no dynamic pressure but only a static pressure that will equal the total pressure, therefore ps = H = pa + 4 p V2. The pressure produced by bringing the air to a standstill at the stagnation point thus exceeds the atmospheric pressure pa by the quantity Уі p V2. But the pressure on the back of the plate is also pa, so at this point there is an excess pressure on the front of the plate.

This argument only applies to the stagnation point, which is the point of maximum pressure on the front of the plate. What happens at other points on the front of the plate as the fluid moves away from the stagnation point and moves toward the edges? The fluid will speed up so its pressure will drop. But the pressure exerted by the moving fluid only drops to atmospheric pres­sure as it reaches the free stream velocity at the edges. It follows that, at all points on the front of the plate, there will be a higher pressure than the at­mospheric pressure on the rear of the plate. On this account, therefore, the forces on the plate do not cancel out, except at the very edges, and there is an overall resultant aerodynamic force on the plate.42

Discontinuous flows of this kind thus avoid the paradoxical-seeming zero-resultant outcome found by D’Alembert, but it is still necessary to ask whether the predicted forces are the right size. It is one thing to avoid a bla­tantly false outcome and another thing to do so by giving the right answer in quantitative terms. The question still remains: Do the forces predicted on the basis of discontinuous flow fully correspond to the observed forces? Quantitative knowledge of the forces on the plate calls for a quantitative knowledge of the speed and pressure of the flow along the front of the plate, not just at the stagnation point and the edges. Until this information could be provided, the picture was merely qualitative. Working independently of one another, Rayleigh and Kirchhoff provided testable answers.43

The quantitative analysis of discontinuous flows was not an easy task, but by the use of ingenious transformations, it proved possible to connect the discontinuous flow around a flat plate to the simple, uniform, horizon­tal flow. There was no guaranteed way to find the required steps leading to the simple flow. It called for a high order of puzzle-solving ingenuity. The character of the thinking required can be glimpsed from the first few steps of the process. Rayleigh and Kirchhoff noticed that in the original flow, the direction of the boundary streamline along the plate was known but not the velocity. For the free streamline, the reverse held: the velocity was known but not the direction. If the flow could be redrawn on a diagram where one axis was proportional to speed while the other axis was proportional to direction, then both parts of the streamline would be transformed into straight lines. This was a step toward the desired simplicity because the straight lines could be interpreted as “polygons” of the kind to which the Schwarz-Christoffel theorem could be applied. Neither Kirchhoff nor Rayleigh explicitly used the Schwarz-Christoffel theorem but used a number of ad hoc transformations to achieve the same goal.44 But once the formula describing the flow had been found, pressures and velocities could be calculated and quantitative predic­tions made.

Rayleigh’s achievement was to generalize Kirchhoff’s analysis, which dealt with plates that were normal to the flow, and give the analysis required for plates that were oblique to the flow. This classic result in hydrodynamics was published in 1878 and provided the starting point for the work of the Advi­sory Committee for Aeronautics when its members tried to explain the lift generated by an aircraft wing. The work was officially overseen by Rayleigh himself as president of the ACA. It was monitored on a day-to-day basis by Glazebrook and other mathematical physicists who were closely associated with Rayleigh. In the next chapter I describe this early British work on the lift and drag of a wing, which was based on the idea of discontinuous flow.