Stream Functions and Streamlines
To apply and solve the Euler equations, mathematicians had to introduce various techniques to relate them to specific flow problems. “As they stand,” said Cowley and Levy, “these equations are not very suitable for solution” (39). They need to be fleshed out. This was done by means of a variety of auxiliary concepts such as source, sink, vortex, and stream function. The general connotations of the labels “source,” “sink,” and “vortex” will be evident, and their mathematical idealization refines, but does not essentially alter, the everyday meaning of the word. A vortex is like a whirlwind around a central point. A source is a geometrical point at which fluid is created at a certain rate, and a sink is a geometrical point at which it disappears and is destroyed. The words “stream function,” however, do not have any obvious counterpart in common usage. In this section I describe briefly what they mean.
Imagine a coordinate system of x – and y-axes that is to be used to describe a flow of fluid. The value of the stream function at some point P is given by the amount of fluid that flows in unit time across a line drawn from the origin to P. To specify this quantity is to specify the value of the stream function. In hydrodynamics this value is usually designated by the Greek letter psi, y. Altering the position of the origin only alters the value of y by the same constant amount at all points in the flow. It follows from the definition that such a function has a simple relation to the velocity components of the flow, and this is the utility of the stream function. If u is the speed along the x-axis at P and v is the speed of flow along the y-axis, it can be shown that
u = -—, and
dy
dw
v ~~dX ■
Given the stream function, a process of differentiation gives the velocity components. Here is a simple example. The stream function for a uniform flow of speed U along the x-axis is
W = —Uy = —Ur sinft
The first expression is in Cartesian coordinates and the second is in polar coordinates, giving the value of у at the point (r, 0). In Cartesian coordinates, differentiating у with respect to x gives the correct answer v = 0, meaning that the flow has zero velocity along the y-axis. Differentiating with respect to y gives the speed u = U along the x-axis. Notice that putting у = c, a constant, gives a straight line parallel with the x-axis. Such a line can be called a streamline of the flow. Later in the discussion it will become evident that, for all its simplicity, this flow plays a basic role in hydrodynamic reasoning. Logically, it provides the foundation of the edifice.
I have referred to a streamline of this basic flow, but what is a streamline? In everyday language the words connote speed. Modern aircraft are “streamlined,” whereas aircraft in the period of the old Advisory Committee for Aeronautics, with their struts and protruding engines and undercarriage, were certainly not. This usage, and the idea of low-resistance, streamlined bodies, was already well established in early aerodynamics, even if it could not be realized in the construction of flying machines.17 The technical meaning of the term “streamline” in hydrodynamics, though related to this popular meaning, is more specific. A streamline drawn through a point in a fluid flow is a line that conforms to the direction of motion of the fluid element that is located at that point at that moment in time. A moment later the point may be occupied by another fluid element with a different velocity. The picture becomes much clearer if the flow is steady so that the speed and direction of the flow at a given point are constant over time. When the flow is steady, then streamlines will coincide with the path taken by the fluid element. Looking at the streamlines will give a picture of what the fluid elements are doing. Streamlines also indicate something about the speed of the flow. For steady incompressible flow they come closer together as the flow speeds up and become wider apart as the flow slows down.18
How does the mathematician identify streamlines in order to draw a diagram of a flow? The answer is by reference to the stream function. Once in possession of an expression у for the steam function of the flow, the mathematician generates a series of curves by putting у = c, a constant, and giving
the constant a sequence of values q, c2, c3, etc. The curves are conventionally plotted at equal intervals. These are the streamlines. As a simple example, recall the stream function for the uniform flow parallel to the x-axis—the basic flow. The formula for the stream function was у = – Uy. Putting у = (say) 0, 1, 2, 3, etc. gives the straight, horizontal lines y = 0, y = -1/U, y = -2/U, y = -3/U, etc. Notice that the greater the speed U, the smaller the gap between the lines. Because, by definition, a fluid element will not cross over a streamline, then any streamline can be selected and interpreted as a solid boundary without this in any way changing the picture of the flow. (It is sometimes said that the fluid bounded by a streamline can be suddenly “frozen” or “solidified” without altering the rest of the flow.) In the present case the line у = 0 can be selected for this treatment. The flow then becomes (that is, can now be regarded as) the uniform flow of an infinite ideal fluid along a flat, smooth wall located on the x-axis.
Other, more complicated, flows call for other, more complicated, formulas for the stream function. For example, there are stream functions for the flow around point sources and point sinks and for vortices. The streamlines of sources and sinks radiate away from, or toward, their center point while the streamlines of a simple vortex are concentric circles. By the expedient of adding the stream functions, the flow can be found for combinations of sources, sinks, and vortices. Shortly I shall give the stream function and the streamlines for another, particularly important flow; for the moment, however, the point to retain is that a streamline is specified by setting the stream function equal to a constant у = c.











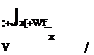 w = Ь£а
w = Ь£а