Looking back to the period of the Great War, after some sixty years, Max Munk expressed the belief that the aeronautical work he had carried out in Gottingen had rapidly fallen into the hands of the Allies. According to Munk, the secret Technische Berichte “were translated in England a week after appearance and distributed there and in the U. S.”3 Exactly how this feat of espionage was performed Munk did not say. Similar stories have been related about the flow of sensitive information in the other direction, from the Allies to the Germans. I have already mentioned the secret testing of the Dunne biplane in the Scottish Highlands before the war. This was said to have attracted the attention of numerous German “spies,” though these stories surely owed more
to John Buchan than to reality.4 A more sober counterpart to Munk’s beliefs is provided by J. L. Nayler, one of the secretaries to the Advisory Committee. Also speaking retrospectively, he said that the wartime Reports and Memoranda produced in Farnborough and Teddington eventually found their way into German hands. Nayler, though, suggested that this took months rather than weeks.5 Perhaps British spies were just superior to German spies.6
The truth was almost certainly more pedestrian than these claims suggest. There is no evidence that agents acting on behalf of the British government got their hands on any information about the wartime Gottingen work and passed it on to their masters in Whitehall or their allies in Paris and Washington. There appears to have been no successful espionage activity. It is not the speed with which information traveled that is striking but its slowness. When information did travel, the channels were overt and obvious rather than mysterious.7 The war had the predictable effect of attenuating the flow of technical information between different national groups, but even during the prewar years, with no military or diplomatic impediments, the flow was surprisingly limited. It is important to identify where the restriction lay. It did not arise because of what might be called material or external factors, such as censorship, but because of more subtle, cultural constraints. It was not the physical inaccessibility of reports, journals, or books that caused the problem. What counted was the response, on the intellectual level, even when they were accessible. For example, both Sir George Greenhill and G. H. Bryan were present at the congress in Heidelberg, in 1904, when Prandtl presented his revolutionary, boundary-layer paper.8 Bryan explicitly mentioned Prandtl’s contribution in his postconference report for Nature, but he ignored its mathematical content entirely and confined his comments to the experiments and photographs.9 It is difficult to resist the conclusion that if such important matters can be passed over in these circumstances, then even if there had been “spies” reporting back to the British Advisory Committee, their efforts would have been wasted.
To reinforce this claim I start with some other prewar events and look at the information that members of the Advisory Committee had available to them about their German counterparts. From the outset the committee, and the Whitehall apparatus that supported it, accepted the principle that it was important to monitor the work of foreign experts. Haldane stressed the point in Parliament, and the theme was picked up by the aeronautical press.10 The commitment to gathering intelligence was made apparent in three ways. First, the preliminary documentation of the committee, when it was established in 1909, included what was, in effect, a reading list for the committee members. The list cited some twenty-two works by French, German, Ital-
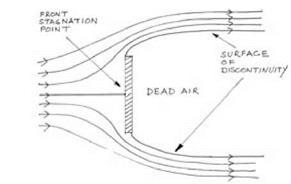
ian, and American writers. The German authors included Ahlborn, Finster – walder, and Lilienthal.11 Second, the sequence of Reports and Memoranda issued by the committee began with a description of the program of German airship research. It was presented by Rear Admiral Bacon at the very first meeting of the Advisory Committee on May 12, 1909.12 R&M 1 consisted of translated extracts from the publications of the German Society for the Study of Airships and included a lengthy quotation from Prandtl.13 There was mention of Prandtl’s wind channel, his experiments on model airships, and, intriguingly, a passing reference was made to his “hydraulic machine” (shown earlier in fig. 7.1). This was the apparatus used to take his boundary-layer photographs. There was, however, no mention of the mathematical theory. Third, and most important of all, the committee was provided with a series of summaries of foreign papers from leading journals such as the Zeitschrift fur Flugtechnik. A steady stream of these summaries was published in the period between the founding of the committee and the outbreak of the Great War, when such material was immediately withdrawn from public circulation.14
A measure of the size of the intelligence initiative can be gathered by counting the number of such abstracts published yearly in the annual report of the Advisory Committee. Such a procedure can only provide an approximate measure of the potential flow of information because it does not take account of the different scope of the individual publications, but it gives some guide. Figure 8.1 charts the year-by-year production of summaries and abstracts of foreign-language publications that were made available to the committee.15 Two things stand out. First, the size of the effort put into tracking foreign work was clearly considerable. Second, there was a consistently high level of attention given to German work, amounting on average to identifying and abstracting some eighteen items per year for a period of six years.
Moving from the quantitative to the qualitative character of the information, it is important to know which authors the committee deemed interesting. The answer is that Prandtl and his collaborators were prominent among them. In December 1910, Glazebrook, as chairman, explicitly drew the Gottingen work to the attention of the members of the Advisory Committee.16 In August 1913, in preparation for a forthcoming visit to the laboratory in Teddington, Prandtl sent a number of his papers to the National Physical Laboratory (NPL) and received acknowledgment from Selby, the secretary.17 Thus, by one route or another, all of the major prewar work of the Gottingen school had been made available, including accounts of the wind channel and the airship work but also material directly concerned with the circulation theory of lift. In addition there were abstracts of papers of indirect interest
|
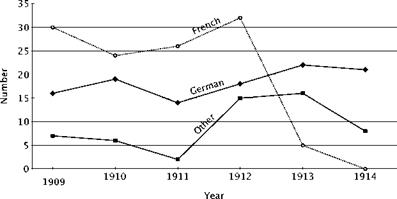
figure 8.i. The number of abstracts of foreign works made available to members of the Advisory Committee for Aeronautics in the years before the Great War. Data from the committee’s annual reports.
|
because of their significance for fluid dynamics in general. More specifically, among the papers summarized, sometimes at length, were those of Foppl on the resistance of flat and curved plates (abstracts 93, 94, 97, 98, 118, and 131), Fuhrmann on the resistance of different airship models (abstracts 95, 96, and 127), and Prandtl’s classic study of the flow of air over a sphere in which he introduced turbulence into the boundary layer by means of a trip wire (abstract 234). Of those explicitly related to the idea of circulation and Prandtl’s wing theory, accounts were given of Foppl’s 1911 study of the downwash behind a wing (abstract 128, but incorrectly attributed to Fuhrmann); Wieselsberger’s 1914 study of formation flying in birds (abstract 276); the 1914 paper by Betz on the interaction of biplane wings (abstract 279); Joukowsky’s pioneering 1910 article (abstract 299); Blumenthal’s 1913 paper on the pressure distribution along a Joukowsky aerofoil (abstract 301); and Trefftz’s 1913 graphical construction of a Joukowsky aerofoil (abstract 302).
The principal mathematical formulas associated with the circulation theory in both its two – and three-dimensional forms were also to be found in the abstracts. Thus the basic law of lift, linking density, velocity, and circulation, L = pvr, was stated, as was the law of Biot-Savart, which was the basis of the three-dimensional development of the theory. The abstracts provided everything that was needed to show that the circulation theory was capable of mathematical development and was more than a mere collection of impressionistic ideas. The abstracts gave clear, documentary evidence of the progress that the German engineers were making. It would appear that the circulation theory was there for the taking. Nevertheless, the availability of the abstracts generated no more enthusiasm for the theory of circulation in its mathematical form than did Lanchester’s original publication with its more intuitive treatment of the subject.
Why might this be? Obviously, the abstracts had no power to force themselves on anyone’s attention. They were things to be used selectively and were subject to the filtering effects of interpretation, both in their composition and their evaluation. Thus Glazebrook’s act in drawing attention to the Gottingen work was probably indicative of his enduring concern with discrepancies between the results of different wind channels and the fundamental problems shared by the NPL and Gottingen in the interpretation of their findings. Gla – zebrook was acutely aware that such problems would be grist to the mill of the “practical men” and was anxious lest they be used to persuade the government to cut the budget of the NPL.18 Furthermore, the precise content of the abstracts reveals the way that reported work may be glossed so that certain aspects of it are given salience at the expense of other readings. Take, for example, the account given in abstract 131, which was devoted to Foppl’s 1910 paper in the Jahrbuch der Motorluftschiff-Studiengesellschaft.19 This paper contained a comparison of Rayleigh flow with Kutta’s theory of circulatory flow. After summarizing the contents of the paper, the abstract writer drew the conclusion that neither approach to the flow over an inclined plate was satisfactory. What was needed was an understanding of certain subtle, viscous effects. “It is suggested that Kutta’s theory throws some light on the experimental results, and in some respects, qualitatively, is in fair agreement with the experiments. At present, however, no entirely satisfactory theory seems to be possible until more is known of the nature of the air flow, the main differences being due to the difficulty of including the frictional effects” (257). The need to include frictional effects was, of course, an abiding theme in the British work. The abstract writer then went on to single out, as the “most striking result” of Foppl’s investigation, “the discontinuity in lift and drift coefficients within the region from 38° to 42°” (258). All the attention was thus directed toward extremely difficult, fundamental, and unstable features of the flow that lay far outside the typical working range of an aerofoil. Once again, the British were drawn to the phenomenon of stalling. The focus was on all the things that could not be understood on the basis of inviscid flow at small angles of incidence rather than on what could be achieved using perfect fluid theory over a limited range. Thus the abstract and summary itself prefigured the selective tendencies and implicit evaluations that worked against the circulatory theory.
The prewar information about German thinking on aerodynamics was rich but unexploited, whereas during the war, the pressure of short-term work added to the tendency to pass over the significance of the German theoretical approach.20 What of the pattern of information flow, and the reaction to it, immediately after the cessation of hostilities? In some quarters in Britain, the outcome of the war produced a jingoistic complacency. Such sentiments were exemplified by C. G. Grey, editor of the Aeroplane, when he said in 1918: “We have nothing to learn from the Hun in aerodynamics.”21 This boast was a continuation of a commonplace theme in the aeronautical press, which, throughout the war, dismissed German inventiveness, originality, and skill.22 Such vulgarity was largely absent from the writing of the more technically sophisticated members of the British aerodynamic community, who had, if not an admiration, at least a healthy respect for German achievements.23 Among the members and associates of the Advisory Committee there was an understandable degree of self-congratulation as the war drew to a close, but it was modest in tone.24
The first reaction to the outbreak of peace by the scientists at the Royal Aircraft Establishment (formerly the Royal Aircraft Factory) was to poke fun at themselves and their critics. The period immediately after the cease-fire, between November and December 1918, saw the production of a light-hearted work titled “The Book of Aeron: Revelations of Abah the Experimenter.”25 This undergraduate-style spoof was composed by the remarkable group of young men who had been recruited by Mervin O’Gorman. Many of them were billeted in a large house in Farnborough called Chudleigh (see fig. 8.2).
|

figure 8.2. The Chudleigh set. Hermann Glauert is seated on the plinth on the extreme left. George Paget Thomson, in uniform, is standing behind Glauert. David Pinsent (left) and Robert McKinnon Wood (right) are seated on the lower steps at the front of the group. W. S. Farren, in uniform, is directly behind McKinnon Wood. F. A. Lindemann is standing behind Thomson, and Frank Aston is seated on the right- hand plinth. David Pinsent was killed in a flying accident on May 8, 1918. From Birkenhead 1961.
|
The house acted as a mess for the RAE and had originally been organized by Major F. M. Green, who, until 1916, had been the engineer in charge of designs.26
The “Book of Aeron,” circulated as an internal report, had been written by a committee that included R. V. Southwell and Hermann Glauert. It was couched in mock, Old Testament terms, with ancient Egyptian overtones, and told the story of the Land of Rae (the RAE), its ruler Bah Sto (Bairstow), and the wicked scribe Grae (C. G. Grey). The Abah of the subtitle appears to be a reference to the designation “Department BA” in which the experimental work was conducted at Farnborough. Naturally, the clash between the aircraft manufacturers (“the merchants”) and the Farnborough scientists (“the men of Rae”) played a significant role in the story. The following passage conveys the spirit of the enterprise:
2. And the men of Rae built air chariots for their king, and brought forth new chariots of diverse sorts; and to each chariot did they give a letter and a number, that the wise men might learn their habits:
3. but the multitude comprehended it not.
4. Then murmured the merchants one to another saying, Why strive the men of Rae so furiously against us? For the king goeth to war with their chariots, and behold our chariots are cast into the pit. (3)
After the relief of the armistice, and the lessening of tension, came the serious business of taking stock. Just what had been achieved during the war? What had been sacrificed, scientifically, because of the demands of the war effort? What, if anything, was to be learned from newly accessible German literature? Bairstow and other committee members rapidly let it be known that they deplored the cutback in basic research that had been caused by the war. In terms of fundamentals, they argued, the period of rapid achievement in aerodynamics had been before the war. It was now time to get back to deeper questions and that meant solving Stokes’ equations of viscous flow. Pure mathematicians may have given up on this task, but new techniques, perhaps using graphical methods, might be developed for this purpose. In a confidential report of November 1918,27 mapping out a program of work for 1919-20, the argument was put like this: “General research in fluid motion has been discontinued during the war and it is very desirable that it should be resumed at the earliest possible moment. It is proposed as soon as the opportunity occurs to continue the study of the motion of viscous fluids to which considerable attention has already been given” (9-10). These sentiments represented the beginnings of a campaign by Bairstow and Glazebrook to channel more resources from short-term to basic research. They argued, in letters to the Times, that government figures for the aeronautics budget conflated the spending on development with that on research proper. This made the expenditure on fundamental work, which was vital for future technology, appear larger than it really was.28
What had the Germans being doing during the war? At first, information filtered through to the British via the French and Americans. In 1919 the American National Advisory Committee for Aeronautics, the NACA, established an office at 10, rue Victorien Sardou in Paris. Their representative, William Knight, actively pursued a policy of information gathering. To the irritation of military and diplomatic circles in Paris and Washington, he made contact with Prandtl and suggested that information on recent developments be shared. Knight contacted Prandtl on November 15, 1919, by letter and managed to get official agreement to visit him in April 1920. He made a second visit in the autumn of 1920.29 It appears to be due to the efforts made in Paris that the British Advisory Committee was furnished with translations of reports by A. Toussant and by Colonel Rene Dorand. Toussant was an engineer at the Aerotechnical Institute of the University of Paris at St. Cyr. In November 1919 he had produced a resume of the theoretical work done at Gottingen based on the Technische Berichte. Extracts of Toussant’s work were translated by the NACA, and these surfaced in February 1920 as a report designated Ae. Tech. 48 for consideration by Glazebrook and his colleagues.30 There was, however, little that Toussant could add to the information that was already at hand from the prewar abstracts. He gave mathematical formulas but none of the background reasoning. Dorand’s report was titled “The New Aerodynamical Laboratory at Gottingen.” It was translated as report T. 1516 in October 1920 and reached the Advisory Committee via the Inter-Allied Aeronautical Commission of Control.31 In Dorand’s report Prandtl was referred to throughout as “Proudet,” but it included three pages of blueprints of the Gottingen wind channels and provided technical details of the automatic speed control and the measuring apparatus. Bairstow felt that there was nothing new in Dorand’s report.32 Others, however, noticed that Prandtl seemed to have solved certain problems that plagued the NPL channels and had “managed to achieve good velocity distribution in the working sections.”33
Both the British and the Americans were keen to locate and translate copies of the Technische Berichte. At a meeting that took place on July 13, 1920, at the Royal Society, minute 28 records Treasury authority for the “employment of abstractors to make abstracts of German technical reports.”34 Across the Atlantic, Joseph Ames, who was the chairman of the Committee on Publications and Intelligence, and one of the founding members of the American National Advisory Committee for Aeronautics, wrote from the NACA headquarters to J. C. Hunsaker at the Navy Department in Washington, D. C., on October 15, 1920:
It is with great pleasure that I am informing you that the National Advisory Committee for Aeronautics has been successful in obtaining a number of sets of “Technische Berichte” and we are mailing you under separate cover volumes No.1, 2 and 3. The Committee is also forwarding a carefully prepared translation of the index of the first three volumes with a list of the symbols used. . . . The importance of the information contained in the “Technische Berichte” cannot be over-estimated and it is the desire of the Committee that all research laboratories and individuals interested in aeronautical research should become familiar with the results of the aeronautical research carried on in Germany during the War.35
The success of this search appears to have been due to Knight’s persistence. He used Prandtl’s good offices to approach the German publishers but had to overcome the numerous obstacles arising from the immediate postwar currency and customs restrictions.36 Meanwhile the U. S. National Advisory Committee continued negotiations with the British about the translation and abstraction of the reports.37 The enthusiastic terms of Ames’ letter, and the continuing efforts by both the British and the Americans, provide a sufficient basis for rejecting Max Munk’s claim that the reports were in the possession of the allies soon after their completion. Had this intelligence already been gathered, all the postwar concern would have been unnecessary.38