The Theory of Ideal Fluids
Physicists, chemists, physiologists, and engineers are all interested in air, and each group studies it from the perspective of its own discipline. In the history of each discipline there is a strand that represents the history of the changing conceptions of the nature of air adopted by its practitioners. Sometimes aerodynamics is counted as a branch of physics and sometimes as a branch of engineering, but however it is classified, it is evident that it involved a determined attempt to relate the flow of air to the basic principles of mechanics. The most important of these are the laws of motion first delineated by Newton, for example, the law that force equals mass times acceleration. The complexity of the air’s behavior, however, means that there is no unique way to connect the flow to the fundamental laws of Newtonian mechanics. How the relation is to be articulated depends on the model of air that is used.
Newton himself treated fluids in different ways at different times. When he was thinking about the pressure of the air in a container, he conjectured, for the purposes of calculation, that air was made up of static particles that repelled one another by a force that varied inversely with distance.4 This concept was a guess that explained some of the known facts, but it was a conception of the nature of air and gas that physicists later abandoned. In its place they adopted what is called the kinetic theory of gases in which it was assumed that a gas is made up of small, rapidly and randomly moving particles. According to the kinetic theory, as developed by James Clerk Maxwell and others, gas pressure is not the effect of repulsion between the molecules of the gas but is identified with the repeated impact of the molecules on the walls of the container.5
When Newton was thinking of a flowing fluid impinging on the surface of an obstacle, he did not use his repulsion model but spoke, for mathematical purposes, simply of a “rare medium” and treated the fluid as made up of a lot of point masses or isolated particles that do not interact with one another.6 The fluid medium was treated as if it were like a lot of tiny hailstones (though this was not Newton’s comparison). Again, the model is not to be identified with the later kinetic theory of gases. The hailstone model, too, dropped by the wayside, though, as we shall see, in certain quarters it still played some role in early aerodynamics. The concept of a fluid that proved most influential in hydrodynamics was different from either of the ideas used by Newton as well as being different from the kinetic theory of gases. The model that came to dominate hydrodynamics, and aerodynamics, was first developed in the eighteenth century by mathematicians such as d’Alembert, Lagrange, the two Bernoullis (father and son), and Euler. They thought of the air as a continuous medium.7
Because the aim was to be realistic, the hypothetical, continuous-fluid picture had to be endowed with, or shown to explain, as many of the actual properties of real fluids as possible. Thus air has density so the continuous fluid must also possess density. Density is usually represented by the Greek letter rho, written p. Empirically, density is defined as the ratio of mass (M) to volume (V), which holds for some finite volume. The number that results, p = M/V, represents an average which holds for that volume at that moment. To apply the concept to a theoretically continuous fluid requires the assumption that it makes sense to speak not merely of an average density but of the density at a point in the fluid, that is, the ratio of mass to volume as the volume under consideration shrinks to zero. If the air is actually made up of distinct molecules, then, strictly, the density will be zero in the space between the molecules and nonzero within the molecules, and neither of these values would qualify as values of the density of the fluid. This dilemma did not appear to be a problem in practice, but it is a reminder that the relation between physical models of the air based on particles and physical models based on a continuum may, under some circumstances, prove problematic.8
Air is also compressible. The same mass can occupy different volumes at different pressures. For many of the purposes of aerodynamics, however, it can be assumed that the density stays the same. This is because (perhaps counter to intuition) the pressure changes involved in flight turn out to be small. The fluid continuum can then be treated as “incompressible.” This approximation only becomes false when speeds approach the speed of sound, which is around 760 miles an hour. In the early days of aviation, when aircraft flew at about 70 miles an hour, compressibility was no problem for wing theory. Things were different for propellers. The tips of propellers moved at a much higher speed, and here compressibility effects began to make themselves felt, but that part of the story I put aside.9
Another important attribute of a fluid is its viscosity, which refers to the sluggishness with which the fluid flows. If a body of fluid is thought of as made up of layers, then the viscosity can be said to arise from the internal friction between these layers. Pitch and treacle are highly viscous fluids, whereas water is not very viscous. Viscosity can be measured by experimental arrangements involving the flow through narrow tubes. The results are summarized in terms of a coefficient of viscosity, which is usually represented by the Greek letter mu, written |4. A highly viscous fluid will be given a high value of |4; a fluid with small viscosity will have a correspondingly small value of |4. Air only has a very slight viscosity. At the extreme, if there were a fluid that was completely free of viscosity, it would be necessary to write |4 = 0. In reality no such wholly inviscid fluids exist, but if the fiction of zero viscosity is combined with the fiction of total incompressibility, this concept can be taken to specify what might be called a “perfect” fluid or an “ideal” fluid.
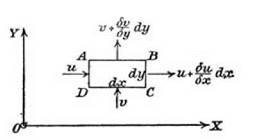
The single most important fact to know about the historical development of wing theory and the aerodynamics of lift is that its mathematical basis lay in the theory of perfect fluids, that is, in a theory in which viscosity was apparently ignored and assumed to be zero. The assumption that air can be treated as an ideal fluid was the cause of much argument, doubt, and frustration, which becomes apparent in subsequent chapters, but its central, historical role is beyond dispute. What turned out to be the most striking developments in aerodynamics (as well as some failed attempts) depended on the idea that viscosity and compressibility were effectively zero. The attractions of this assumption were twofold. First, it seemed highly plausible, and second, it produced an enormous simplification in the mathematical task of describing the flow of a fluid. The exercise produced a set of partial differential equations that determined the velocity and pressure of the fluid, provided that the starting conditions of the flow and the solid boundaries that constrain it are specified. The equations were developed by imagining a small volume of fluid, called a fluid element, and identifying the forces on it. The forces derive from pressure imbalances on the surfaces of the fluid element.
Fluid elements, it must be stressed, are mathematical abstractions rather than material constituents of the fluid. They are not to be equated with the molecules that interest chemists and physicists or the particles that feature in the kinetic theory of gases. The equations of flow do not refer to the hidden, inner constitution of fluids. The reality that is described by the differential equations that govern fluid motion concerns the macrobehavior offluids rather than their microstructure. The abstract character of a fluid element is evident from the way it is typically represented by a small rectangle. The simple geometry of the representation derives from the mathematical techniques that are being brought to bear on the flow. These are the techniques of the differential and integral calculus.10 The concept of a fluid element is the means by which these techniques can be used to gain a purchase on reality. The differential equations that were the outcome are called the Euler equations. They can be said to describe in a strict way the flow of an ideal fluid, but the hope was that they would also describe, albeit in an approximate way, the flow of a real fluid, air, whose viscosity is small but not actually zero.
To give a feel for the style of thinking that went into the classical hydrodynamics of ideal fluids (and, later, into aerodynamics), I shall give a simple, textbook derivation of the Euler equations. It is the kind of derivation that was wholly familiar to many of the actors in my story, and certainly to those who worked in and for the Advisory Committee for Aeronautics. The discussion in the next section is therefore slightly more technical. It is based on the treatment given in one of the standard works of early British aerodynamics, namely, W. H. Cowley and H. Levy’s Aeronautics in Theory and Experiment that was published in 1918.11 Both Cowley and Levy worked at the National Physical Laboratory. Levy had graduated from Edinburgh in 1911, visited Gottingen on a scholarship, and had then worked with Love in Oxford. During the Great War he had been commissioned in the Royal Flying Corps but was seconded to the NPL. As a left-wing activist who wanted to unionize his fellow scientists, his relations with Glazebrook were not of the easiest. After the war Levy left to join the mathematics staff at Imperial College, where he was eventually awarded a chair.12 Cowley stayed at the NPL and worked on problems of drag reduction with R. J. Mitchell, who was designing the racing seaplanes that won the Schneider Trophy for Britain in 1929 and 1931.13