Lamb’s Hydrodynamics

Sir Horace Lamb’s famous textbook started life in 1879 as A Treatise on the Mathematical Theory of the Motion of Fluids, which was based on the lectures Lamb had given as a fellow of Trinity.11 Lamb (fig. 5.1), who had been taught by Stokes and Maxwell, left his Cambridge fellowship in order to marry. He took a chair at Adelaide and then taught for many years at the Victoria Uni­versity of Manchester. He returned to Trinity in 1920 as an honorary fellow. During this time the small Treatise was renamed Hydrodynamics and grew into the imposing volume known to generations of students in applied math­ematics. It went through a total of six editions between 1879 and 1932. The gap between the third and fourth editions, that is, from 1906 to 1916, covered the pioneering phase of aerodynamic theory and the emergence of the circula­tion theory of lift. Most of this aerodynamic work was too late for inclusion in the 1906 version but found a response in the updated 1916 volume. Here, for the first time, one finds the names of Kutta, Joukowsky, Prandtl, Foppl, von Karman, and Lanchester.

The structure of the 1916 edition was very close to that of the previous editions. The new work on aerodynamics was not allowed to upset the pre­existing framework of hydrodynamic theory.12 Consider the relation between the accounts of viscous and inviscid flow. The book was some 700 pages long, and the discussion of viscosity began on page 556 with chapter 11. Viscosity, said Lamb, is a phenomenon “exhibited more or less by all real fluids, but

figure 5.1. Horace Lamb (1849-1934). Lamb was a pupil of Stokes’ at Cambridge and the author of Hydrodynamics, the leading British treatise on fluid dynamics. (By permission of the Royal Society of London)

which we have hitherto neglected” (556). Up to that point all the analysis had concerned an ideal fluid. The Euler equations had been sufficient to solve the problems discussed in the previous chapters, but it was now necessary to con­front the formidable Stokes equations of viscous flow. The equations, which Stokes had arrived at in 1845, were duly derived and set out on page 573. I give a form of the equations below. I have simplified them and changed Lamb’s notation slightly so that they can be compared more easily with the Euler equations for ideal fluids as I gave them in chapter 2. Like the Euler equations, they are partial differential equations that relate together the components of fluid velocity u and v and pressure p, but this time allowance has been made for viscosity represented by |i. Stripping away the negligible effect of external forces such as gravity and treating the fluid as incompressible, and the flow
as both two dimensional and steady, the Stokes equations for a viscous fluid can be written as follows:

dp ( du du і ^2 ,

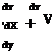-^ = ^1 u— + v— — u and dx ^ dx dy)

where

If the coefficient of viscosity, |i, is put equal to zero, the equations lose the terms on the extreme right and they assume the simpler form of the Euler equations for an ideal fluid. This does not mean that any solution to the Euler equations is also a solution to the Stokes equations. The presence or absence of the viscous terms alters the character of the equations. The Euler equations do not have to satisfy all the boundary conditions of the more complicated equations. A solution to the equations of viscous flow must satisfy the condi­tion that the fluid adheres to any solid boundary and thus has zero velocity along the boundary as well as zero velocity normal to it. An ideal fluid is not required to adhere to a solid boundary but can slide along it with perfect smoothness.

After the derivation of the Stokes equations, Lamb considered a num­ber of applications, for example, the flow of a viscous fluid between two flat plates that are very close together, and the motion of a sphere falling through a very viscous fluid. The former case approximates the study of lubrication. It also provided the occasion for Lamb to discuss the intrigu­ing photographs taken by Hele-Shaw. These rendered with great accuracy the appearance of the flow of an inviscid fluid. By introducing a (very thin) cylinder between the plates, and forcing the fluid to flow around it, the flow could be studied even in cases that defied direct mathematical analysis. Lamb recapitulated the mathematical explanation of these photographs first given by Stokes. Stokes had been able to demonstrate why a viscous flow could, under the circumstances of creeping flow, simulate the behavior of an inviscid flow.13

The case of the sphere falling through a viscous fluid was important for the study of meteorological phenomena that involved droplets of water in
the atmosphere.14 Because the drops fell very slowly, it was possible to sim­plify the equations and arrive at a law giving their speed. In 1910 this law had been applied to the oil droplets in Robert Millikan’s famous experiment to measure the unit of electric charge. The oil drops in the apparatus obeyed Stokes’ law, as it came to be called, which gave their speed of fall in terms of their radius, relative density, and the coefficient of viscosity of the fluid.15 Lamb showed how this law was derived from the basic equations. Important as these and similar results were, the introduction of viscous forces into the analysis had to be accompanied by a corresponding limitation in the role played by the inertial forces. The motions under study had to be very slow or the dimensions very small. Without this restriction the Stokes equations were, in general, intractable.

The 1916, fourth edition of Hydrodynamics contained a new section, “Re­sistance of Fluids,” which Lamb added to the end of the chapter on viscosity. It was here that he addressed the aeronautical work. The location and the name of the new section suggest that Lamb saw the problem of lift as falling under the rubric of viscous flow. The position and title carried the message that lift was not to be analyzed on the basis of perfect fluid theory. Resistance, said Lamb, “is important in relation to many practical questions” (664). He mentioned the propulsion of ships, the flight of projectiles, and wind forces on, for example, buildings, and added that although resistance “has recently been studied with renewed energy, owing to its bearing on the problem of artificial flight, our knowledge of it is still mainly empirical” (664).

Lamb then discussed Kirchhoff-Rayleigh flow and drew attention to its empirical failings, particularly the failure to account for the suction effect on the upper surface of a wing. The reader was referred to publications by Stan­ton and Eiffel for information on “the experimental side.” After this came an account of the circulation theory. It was introduced as an explanation of how a body may be supported against gravity that had been “put forward from a somewhat different point of view,” that is, somewhat different from the theory of discontinuous flow (666). A footnote then made reference to Lanchester’s Aerodynamics, but no attempt was made to expound Lanchester in his own terms. Instead the reader was briskly referred to the earlier sec­tion in Hydrodynamics, article 69, which dealt with Rayleigh’s tennis ball. Lanchester’s theory, said Lamb,

is based on the result of Art. 69, where it was shown that a circular cylinder will describe a trochoid path, the motion being mainly horizontal, if the sur­rounding fluid is frictionless, and its motion irrotational, provided there is a circulation (к), in the proper sense, about it. In particular the path may be a

horizontal straight line, the lifting force (which is to counteract gravity) being

then

Y = KpU

per unit length, where U is the horizontal velocity. (666)

Lamb went on to show that the formula held for a cylinder of any cross section, not just for the case of a winglike section. Here Kutta and Joukowsky were mentioned and references given. Lamb then cited the result for an el­liptic cylinder (that is, the 1910 Tripos question) and went on to say that Kutta “had treated the case of a lamina whose section is an arc of a circle.” Lamb’s summary is instructive: “He [Kutta] assumes the circulation to be so adjusted in relation to the velocity of translation that the infinite value of the fluid velocity which would otherwise occur at the following edge is avoided, whilst an infinity remains of course at the leading edge. It is supposed that in this way an approximation to actual conditions is obtained, the ‘circulation’ rep­resenting the effect of the vortices which are produced behind the lamina in real fluids; and a good agreement with experiment is claimed” (667).

All the standard British objections found an expression in this compressed passage. Kutta’s theory was not offered as a description of reality. There was merely the supposition that there was some “approximation to actual condi­tions.” In a real fluid there are vortices in the flow behind a lamina, but these received no recognition in Kutta’s analysis. The circulation (in quotation marks) merely represents the effects of a certain phenomena but (the wording implies) does not correspond to its real nature.

It would be difficult to devise a description of Kutta’s work that was as brief and as accurate as Lamb’s but that contained more qualifications and implied question marks. Perhaps this was to be expected, given that the dis­cussion of Kutta’s inviscid analysis was located in a chapter devoted to vis­cous processes. The message was that Kutta, Joukowsky, and Lanchester were trying to represent essentially viscous processes by an inviscid theory. Lamb was highlighting the artificiality of their analysis and pointing to the need to ground it in Stokes’ equations of viscous flow.