Idealization as the Route to Realism

Prandtl took a significant step toward greater realism when he went be­yond the idealization of the infinite wing. But, as von Mises emphasized, Prandtl’s own work rested on numerous idealizations. Prandtl was fully aware of this. He explained, for example, that the lift force was assumed to be small so that changes in the direction of the airflow would also be small. Mathematically this justified the neglect of all but the lowest order of the quantities under consideration and made the theory linear. As we have seen, the wing was replaced by a bound vortex, a lifting line, and was treated as if it had no chord. Central to the process of idealization was the now familiar horseshoe vortex. The metaphor of the horseshoe is strained be­cause the vortices in Prandtl’s model were in the form of straight lines with right-angled bends, whereas horseshoes are curved. How did the schemati – zation acquire this inappropriate name? The answer links together some of the sparse facts about the relation between Prandtl’s work and Lanchester’s book. It also provides material for reflecting more generally on the role played by idealization.

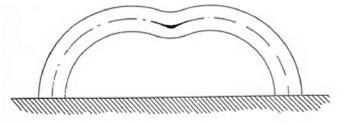
In Lanchester’s Aerodynamics there is a drawing of the vortex system around, and behind, a wing (175). Lanchester’s sketch is reproduced here as my figure 7.14. The likeness is not exact, but Lanchester drew the vortices in a way that looked roughly like a horseshoe. They are certainly much more horseshoe-like than the vortex system made up of the three straight lines that Prandtl used. Although Lanchester himself called the shape a “hoop or half­ring” (174), this description must have been the origin of the “horseshoe” metaphor. The Hufeisen label presumably arose in Gottingen as a natural response to Lanchester’s truly horseshoe-like figure.

Prandtl knew Lanchester’s book, and he knew Lanchester’s drawing. He mentioned it explicitly in one of the few reflective pieces he wrote

about his methods of work. In a talk he gave in 1948, called “Mein Weg zu hydrodynamischen Theorien” (My route to hydrodynamic theory), he re­marked that it was frequently his doubts about existing treatments of a prob­lem that spurred him to new ideas—and he instanced this particular diagram in Lanchester’s book as an example.84 Unfortunately, he did not specify exactly what it was about the figure that struck a discordant note. A probable answer is that the figure looked wrong because Prandtl took it to be a consequence of Helmholtz’s theorems that the trailing vortices would be carried along by the streamlines and, to a first approximation, these would be the straight stream­lines of the free flow. The free-vortex lines would not coincide exactly with a prolongation of the original, straight streamlines (because they would have a slight downward movement), but they would not have the marked, outward curving, horseshoe-like shape attributed to them by Lanchester.85 The defect in Lanchester’s figure was removed in the better, though still approximate, straight-line diagram that Prandtl subsequently used. This showed the trail­ing vortices going straight back from the wingtips.

Was the error in Lanchester’s figure obvious to Prandtl the moment he set eyes on the original diagram, or did it take some time before the problem emerged into view? There are grounds for thinking that the error may not have been immediately obvious. The horseshoe-like diagram was not modi­fied in the German translation of Lanchester’s book made in 1909 by Prandtl’s friends Carl Runge and his wife. Had the diagram seemed obviously wrong from the outset, Prandtl would have mentioned it to his friends, and the mat­ter would have then been raised with Lanchester in the discussions that took place in Gottingen over the translation. The opportunity would have been taken to modify the text in the same way that an opportunity was taken to add a mention of Prandtl’s 1904 boundary-layer paper.

Although Prandtl introduced his quantitative theory in 1910, in the sum­mer semester of 1909 he had already given a series of lectures on the scientific basis of airship flight in which, in addition, he had touched, qualitatively, on the circulation round the finite wing of an aircraft. Some of Otto Fop – pl’s notes of those earlier lectures have survived and are reproduced in Ju­lius Rotta’s beautifully illustrated book Die Aerodynamische Versuchsanstalt in Gottingen.86 Foppl’s lecture notes include a diagram that he presumably copied from one of Prandtl’s own blackboard drawings. The diagram shows the vortices curving out from the wingtips in the way Lanchester had origi­nally presented them. It seems that in 1909 Prandtl had drawn the vortex sys­tem so that it did indeed still look like a real horseshoe. Foppl’s diagram also contains a cross section of the trailing vortices that clearly shows the core of the vortices separated by a distance considerably greater than the wingspan, thus confirming the idea that the vortex lines were not meant to go straight back from the tips. The mere presence of the diagram does not prove that Prandtl had drawn it on the board as an example of truth rather than error, but a probable sequence of events would be this: Prandtl started by accept­ing the (curved) horseshoe picture, as did Finsterwalder, but within a year realized that it was wrong. Henceforth his model had straight lines. Despite this change of mind, the name Hufeisen appears to have stuck and was used, somewhat incongruously, for the simple, straight-line vortex schema that re­placed the original curved horseshoe.87

I shall now comment on the important transition from the simple, straight-line horseshoe schema to the refined version involving an infinite number of infinitesimal horseshoe vortices. The infinity of vortices coming away from the trailing edge creates a “vortex sheet” spread across, and trail­ing behind, the span of the wing. In the simple schema there was a vortex line coming from each tip; now there is something like a continuous train of vor – ticity attached to the rear of the wing. This changes the picture considerably. It also poses a problem. If this picture is right, the earlier picture was wrong, but the supporters of the circulatory theory claimed to have actually seen the simple horseshoe structure. In the first publication to use Prandtl’s theory, Foppl said that the two vortices trailing from the wingtips had been made visible in the wind channel by introducing ammonia vapor. Nor was it just the members of the Gottingen group who claimed to have seen the horse­shoe-like vortices. A similar, though more guarded, claim had been made by Lanchester, who had moved a model aerofoil under water and claimed to have “traced experimentally” the vortices that were postulated in his theory.88 But if these two trailing vortices are now discarded as theoretical fictions, what was it that had been made visible? One possible answer, according to later versions of the theory, was that the phenomenon reported was really

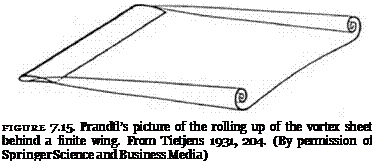the rolling up of the vortex sheet. Prandtl argued that the sheet was unstable and rolled up at the edges in the way shown in figure 7.15. The rolled-up sheet then decayed into something resembling the two trailing line vortices. Per­haps this is what had been seen.89

There remains a further and deeper question about the move from the single, horseshoe vortex to the infinite number of trailing vortices that now constitute the vortex sheet. I have explained that the single, horseshoe schema could not do justice to what was known experimentally about the distribution of lift along a wing. Greater realism required a non-uniform lift distribution across the span, with zero lift at the tips. Accordingly, Prandtl replaced his single, highly abstract, horseshoe model with an infinite number of similar models. No fundamental principle of the original model was changed in the course of producing the more refined version. In fact, those principles were reproduced an infinite number of times. Can this be right? Can an unrealistic construct be made more realistic by repetition? The refined horseshoe model shows that the answer to this question must be yes.

The earlier discussion of Prandtl’s boundary-layer theory showed that the realism of a theory may be increased even though physically impossible ide­alizations were still present. Now the point can be taken further. Realism may be increased by increasing the number of idealizations. It may sound wrong to say that “realism” is increased, while attributing that increase to the in­creased use of highly “unreal” instruments of thought, such as ideal fluids and infinitesimal vortices, but the discomfiture must be overcome. The essential point is that there is no valid inference from the desirability of greater realism, as that word is normally understood, to the undesirability of idealization. If a theory has been made more realistic, it does not follow that abstractions and idealizations must have been removed or their number diminished. This might, on occasion, be part of the story, but the move to greater realism bears no necessary relation to a reduced number of abstractions and idealizations.

Prandtl and his colleagues were not inclined to be apologetic about the abstractions they deliberately introduced into their theory, nor were they in any doubt that they were grasping reality. As Prandtl insisted to his Ber­lin friend von Parseval, the Gottingen work on vortex theory was successful because of its abstractions, not in spite of them. In discussing a paper that von Parseval had given on the formation of vortices on a wing, Prandtl com­plimented von Parseval on his treatment but contrasted their approaches.90 He put it like this: “Herr Professor v. Parseval hat der Wirbeltheorie, die bei unseren eigenen Arbeiten immer etwas Abstraktes behalten hat (die allerdings gerade durch die bewufit eingefuhrten Abstraktionen zu ihren Erfolgen fuhren konnte), eine anschauliche Deutung gegeben” (63) (Prof. v. Parseval has given an intuitive significance to the theory of vorticity. In our own work it has always been treated rather abstractly [though it is, neverthe­less, precisely because of these consciously introduced abstractions that it has led to success]). Prandtl’s assistant Max Munk surely spoke for the Gottingen group as a whole when he insisted that the formulas of Prandtl’s wing theory represented “die wirkliche auftretenden Vorgange”—“the actual processes that occur.”91 The consciously introduced abstractions were the means by which the real and actuality occurring processes were described.

The stance of Prandtl and Munk, and the striking achievements of the Gottingen approach suggest a bold generalization. Perhaps successful work of this kind will always be based on idealizations and abstractions. If this is cor­rect, then what is really at issue is not whether abstractions are to be used but which abstractions are to be used. Which are to be counted as having a role in the laws of nature and which not? Scientists and engineers themselves, collec­tively, have the responsibility of according or withholding that status and of saying which abstractions and idealizations best describe the actual processes that occur in nature. Different groups may discharge this responsibility in dif­ferent ways. This fact has already been encountered in the different positions adopted by British and German experts with regard to the Stokes equations. Now we have another example. For the German aerodynamic community, unlike the British, the pragmatic success of the circulatory theory of lift, even within a limited technological domain, was evidence enough that the gulf between thought and reality was being overcome.