Assessing Taylor’s Argument
What is the correct understanding of Taylor’s “Note on the Prandtl Theory” and the mathematical arguments he put forward? What might explain the inversion of its perceived significance? Why did Taylor himself begin that process when he reworked the conclusion to the original note in his published appendix? Clearly, Taylor was not trying to rehabilitate the old discontinuity theory; he was merely using it to embarrass the supporters of Lanchester and Prandtl. He was showing that there was no unique explanation of the phenomena summarized by the Kutta-Joukowsky law.22 Taylor can therefore be seen, at least initially, as putting forward counterexamples in order to make a logical point. He was concerned with what follows, or does not follow, from the standard formulation of the circulation theory of lift. He had caught Glauert out in a hasty inference, but to show that proposition A does not
|
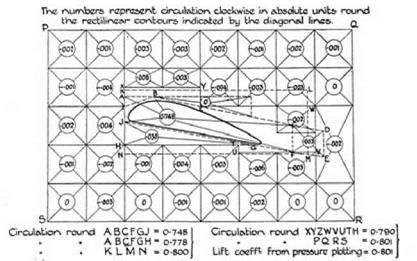
figure 9.4. The contours and circulation studied in Bryant and Williams’ experiment. Notice the parts of the contour line around the wing, such as CF and LM, which cut through the flow behind the wing and do so at right angles to the main flow. From Bryant and Williams 1926, 209. (By permission of the Royal Society of London) |
entail proposition B does not prove that B is false. Taylor’s argument did not establish the falsity of the conclusions that Glauert drew about the results that were emerging from Bryant and Williams’ experiment.
As well as measuring the circulation along contours that enclosed the wing, Bryant and Williams also measured the circulation around contours that did not enclose the wing. This part of their argument remained intact. They divided the space around the wing into zones, like tiles on a bathroom wall, and then measured the circulation around each zone (see fig. 9.4). The question they posed was the following: Were these local circulations all zero? Zero circulation was required for these contours (that is, contours not surrounding the wing) because that would indicate that the main flow was irrotational, namely, an irrotational motion but with circulation around the wing. Not all of these local circulations turned out to be zero. As can be seen in figure 9.4, there were a number of anomalous values particularly among those recorded near the leading edge. Despite this, enough of the readings were sufficiently close to zero for the measurements to be seen as a vindication of the theory. This result had emerged after Glauert’s preliminary analysis and after Taylor’s original note. It was therefore too late to have played any role in the exchange in the Aerodynamics Sub-Committee, but it was acknowledged in the published version of Taylor’s note attached to Bryant and Williams’ paper in the Philosophical Transactions.
The new data may have contributed, in some measure, to the change in Taylor’s tone between the unpublished and the published versions. Despite limitations in the experimental design, the overall picture that emerged from the experiment favored the circulation theory. Taylor therefore had little choice but to begin the published version of his comments by accepting that, after all, the flow was mainly irrotational. As he put it: “In their paper ‘An Investigation of the Flow of Air Round an Aerofoil of Infinite Span,’ Messrs. Bryant and Williams show that the flow round a certain model aerofoil placed in a wind channel is not very different from an irrotational flow with circulation. There are, however, differences which are considerable in the wake, a narrow region stretching out behind the aerofoil” (238).
The acknowledgment that the flow outside the wake was “not very different” from irrotational gave the supporters of the circulation theory all they really needed. Taylor had himself identified this as “Prandtl’s fundamental hypothesis,” but though he was now conceding the point he did not linger on the concession. Taylor immediately drew attention to the flow inside the wake, which was nonirrotational. This point was the real focus of his interest. The Aerodynamic Sub-Committee discussions of the preliminary data coming from Bryant and Williams, in December 1923, had charged Taylor with the task of differentiating “between the effect due to circulation and that due to eddying on the forces as measured on a complete aerofoil.”23 The “Note on the Prandtl Theory” was his response to this request. In the same spirit, when Bryant and Williams gave their technical report to the committee, Taylor drew attention to the apparent presence of local areas of significant circulation where there should have been none. Glauert, by contrast, wondered if this result could be an artifact produced by the compounding of small errors elsewhere in the data.24
In taking the line he did in his note, Taylor showed that his thinking fell into the familiar pattern that was characteristic of British work—with the exception of Glauert’s. Taylor’s counterexamples were an expression of the old argument that perfect fluid theory must be false because it predicted zero drag for an infinite wing. The wake was the physical source of the drag, and drawing attention to it and exploring the consequences of its presence, merely underlined the standard objection. If, along with a wake and a viscous drag, the Kutta-Joukowsky law of lift turned out to be approximately true of the flow, then some other reason had to be found to explain the law than the one originally advanced. In a real, viscous fluid, there was no well-defined quantity that could be called “the” circulation of the flow. The value of the relevant integral would not be contour-independent but would, in general, vary from contour to contour. This was why Taylor stressed the contour dependence of the experimental results. Taylor, however, was not asserting anything that the defenders of Prandtl’s theory had not granted long ago. In 1915 Betz had made a correction to allow for the role of the wake. There was no inconsistency between what Taylor said in the passage quoted earlier, in which he conceded the generally irrotational nature of the flow, and what Glauert had said originally in his technical report “Aerofoil Theory,” in which he had conceded a viscous wake. Both men acknowledged the presence of rotational and irro- tational flow in the phenomenon before them. The difference between them lay in their reaction to this agreed fact. It was a difference of emphasis and preferred method. Taylor wanted to know where the inviscid approach failed, whereas Glauert wanted to know where it worked. Taylor’s eyes were directed to the viscous wake, whereas Glauert’s gaze was on the nonwake.
This concern with the wake may help explain the inversion that took place in the perception of Taylor’s argument, and even why Taylor himself reexpressed his original, negative point in an oddly positive way. The ideas Taylor used, negatively, to construct the counterexamples to the circulation theory became resources that could be used, positively, to study the wake. This study rapidly became a subject of research in its own right. The ideas Taylor originally advanced as counterexamples found a new use. Perhaps it was the transition to this new role that gave rise to the later misunderstanding. The new studies of the wake did not displace the circulation theory of lift but came to complement it. The viscous flow inside the wake found a place alongside the inviscid flow outside the wake. Nor did the two merely coexist. Rather, the latter could be seen as the limiting case of the former. As the wing increases in efficiency, so the wake gets smaller. In the limit the wake is simply the vortex sheet behind the wing, which was central to Prandtl’s analysis. Taylor’s viscous, rotational wake becomes, to use Glauert’s word, “evanescent.” Understood in terms of Glauert’s methodology, the reality of the wake was not being ignored but was allowed for in the limiting process by making the right choice of the inviscid flow. The counterexample then becomes identical with the phenomenon it was meant to contradict. Perhaps Glauert had begun to convince Taylor that the seeming contradiction between his counterexamples and the theory were not as logically sharp as it first appeared. Glauert would surely have discussed the problem with Taylor in the time between Taylor’s (unpublished) note and his (published) appendix. If minutes had been taken of these discussions, it might have been possible to trace the process by which Taylor came to reformulate his original doubts.
What is a matter of public record is how Taylor’s argument was deployed for the purpose of studying the wake. Recall that Taylor’s analysis of momentum relations concerned not only lift but also drag. The physical basis of Taylor’s calculation of drag was the idea that drag arises from a loss of momentum in the fluid flow behind the obstacle. His analysis showed that this loss implied a pressure reduction in the wake, namely, a diminution of the quantity called the “total head” or the “total pressure.” (These terms were explained in chap. 2 in connection with Bernoulli’s theorem.) This account of drag was taken up by Fage and Jones at the National Physical Laboratory in a paper published in 1926 in the Proceedings of the Royal Society.25 They cited Taylor’s comments on Bryant and Williams’ work, but they did not read them negatively. They understood them as positive suggestions about the nature and measurement of drag and proceeded to do the experiments needed to test them. Bryant and Williams, they said, had explored the velocity of the flow in the wake of a model aerofoil spanning the wind tunnel and had shown that, for all practical purposes, it was two-dimensional. They went on: “In an Appendix to the above paper [by Bryant and Williams], Prof. G. I. Taylor shows that there is good reason to believe, on theoretical grounds, that the drag of an aerofoil can be determined with good accuracy from observation of total-head losses in the wake, provided that these observations are taken in a region where the velocity disturbances are relatively small” (592). Fage explained that the drag under discussion was not Prandtl’s “induced drag,” which was a by-product of the lift, but “profile drag” associated with the shape and attitude of the wing section (592).
Fage and Jones’ experiment was to be carried out on an infinite wing with two-dimensional flow for which the induced drag should be zero. Using the symbol H to represent the total head ^p+1 pq2 j and, like Taylor, neglecting small quantities, Fage and Jones rewrote Taylor’s drag equation in a simplified form as
D = pjH. ds,
C
where “the integration is taken along a line passing through the wake at right angles to the undisturbed wind direction” (594). Outside the wake, H will be constant from streamline to streamline but will vary as the line of integration passes through the wake. For a contour that cuts the wake parallel to the y – axis, the value of the direction cosine l is unity, which explains its apparent absence from Fage’s simplified expression. If Taylor’s analysis was right, the experimenter could measure the drag on a two-dimensional or infinite wing by summing up the losses in the total head across the span. This was what Fage and Jones did using a model wing of 0.5-foot chord mounted, with only a small clearance, right across the 4-foot wind tunnel. The wind speed was 60 feet per second. They calculated the drag from pressure measurements taken in the wake and performed the required integration using graphical methods. They found that most of the loss of total head pressure (H) came from a loss in velocity (q) rather than a reduction in the static pressure (p) of the wake. Finally they compared the predicted drag with the result of their direct drag measurements when the wing was suspended on wires and attached to scales. The two methods they concluded were “in close agreement” (593).
A further feature of Taylor’s argument that was given a new employment was his picture of the equal discharge of positive and negative vorticity into the wake (respectively from the upper and lower surfaces of the wing). This also helped to integrate the circulation theory into the study of viscous flow.26 The theorem that the circulation in all circuits enclosing the aerofoil had the same value, if the contour cut the wake at right angles, was, as one later researcher put it, “of fundamental importance in the calculations of the lift of aerofoils allowing for the boundary layer.”27 An important sequence of papers starting in the mid-i930s was devoted to this theme, and they all traced their approach back to Taylor’s appendix. New ways were sought to generalize the old Kutta condition in order to quantify the circulation under more complex and realistic conditions.28
As independent evidence in favor of some version of the circulation theory increased, the original significance of Taylor’s analysis, as a source of counterexamples, decreased. The ideas became consolidated in a new context. This may explain why von Karman and Burgers expressed themselves as they did. Perhaps they were not misreading Taylor so much as rereading him. That is, they were reinterpreting his original contribution in the light of later concerns and assimilating his ideas to the new preoccupations of a research agenda in which the circulatory theory of lift was taken for granted. Taylor’s line of thought was now being used to supplement rather than undermine the theory of circulation.