The Basis of the Circulation Theory

Within the framework of Newton’s mechanics, the flow of air around an air­craft wing can only support the weight of the aircraft if the flow generates a force that is equal and opposite to that of the weight. In level flight the upward force, the “lift,” must be in equilibrium with the downward force of gravity. Expressed in terms of fluid dynamics, the lift must be the result of air pressure on the wings. There must be an overall pressure imbalance between the upper and lower surfaces of the wing. The pressure of the moving air on the upper surface of the wing pushes downward. This must be surpassed by the pressure on the lower surface of the wing which pushes upward. It is the excess of the upward over the downward pressure that constitutes the lift and is therefore the central fact to be explained. It cannot be assumed that the resultant downward pressures and the resultant upward pressures act through the same point. In general they will not; the pressures on the wing will not only have the capacity to produce a lift, but they will also generate a turning moment that causes the wing to pitch. These pitching moments played a significant role in the analysis of stability carried out by G. H. Bryan. In what follows, however, I am mainly concerned with the resultant lifting effect of the pressures on the wing. I have already introduced Bernoulli’s law which implies that, if the air behaves like an ideal fluid, then the faster the air flows over the wing the lower will be the pressure it exerts, and the slower the flow the higher the pressure. If it is also accepted that the airflow around a wing is not discontinuous Rayleigh flow but follows the surfaces of the wing, then the problem of lift is simplified. It reduces to that of explaining why the air immediately below the wing is moving more slowly than the air immedi­ately above the wing.

Here it is necessary to avoid a popular misconception. A cross section of a typical wing has a flat base and a curved upper surface. The airflow di­vides at the leading edge, and some air takes the upper route over the curved surface while some takes the lower route along the flat and straight surface. Looking at such a shape, one can easily imagine two molecules of air parting company at the leading edge and joining up with one another again at the trailing edge. Like two travelers they wave farewell at the parting of the ways and then shake hands when they meet up later. But the low road is straight while the high road is circuitous, so the traveler who took the high road must have sped along more swiftly in order to meet up with the traveler who took the shorter path. Is this how it is with the air? Equal transit time plus a path difference certainly implies a speed difference, but this is not the secret of the wing.3 The questionable assumption is that the traveling companions, that is, the two molecules, meet up again. There are decisive reasons why this theory cannot be right. First, the increase in speed necessary to pass over the curved, upper surface of the wing would not generate the observed amount of lift. The path difference is not great enough. Second, the theory would have the conse­quence that an aircraft could not fly upside down. Once inverted, the curved surface would become the lower surface. The theory would then imply that the aerodynamic force would reinforce gravity rather than counteract it. But aircraft can fly upside down, so the theory cannot be right.4 This false theory, based on path difference and equal transit time, must not be confused with the circulation theory of lift. The circulation theory offers a very different account of the speed differences above and below a wing, as I shall now explain.

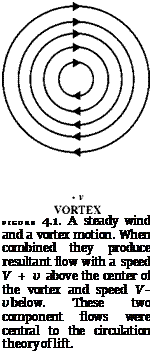
The flow of air over the cross section of a wing is a complicated phenom­enon, but, argued the supporters of the circulation theory, it can be thought of as built up out of two, simple flows. These are (1) a steady wind of constant speed and direction, and (2) a swirling vortex that goes round and round a central point. The two components are shown separately in figure 4.1. I dis­cuss each component flow in turn and then explore the flow that arises when they are superimposed on one another. The steady wind arises from suppos­ing a steady, relative motion of the wing and the air. In reality the air is sta­tionary and the wing moves, but, as previously noted, aerodynamic processes are frequently described in terms of the situation in a wind channel where it is the air that moves. Let the steady wind have a constant speed V and move horizontally. At any given point the flow can be represented by a vector, that is, an arrow pointing in the direction of the flow whose length is proportional to the speed. All the vector arrows representing the steady wind are therefore of the same length and can be assumed to lie horizontally, as shown in the figure. The streamlines of the flow are then equally spaced horizontal lines.

+ V

STEADY

WIND

The vortex flow is more complicated, but the early work on aerodynamics was confined to a particularly simple form of vortex. Let the vortex swirl in a clockwise direction around a central point that is assumed to be in a fixed po­sition. Unlike a normal vortex, in water or air, this one is not carried along by the stream. This special sort of vortex came to be called a “bound” vortex. All the streamlines in the vortex flow have the form of concentric circles. The fluid elements at any given distance from the center of the vortex are assumed to move with the same, constant speed around one of these circles. The elements do not get drawn into the center of the vortex. This is expressed by saying that they have a constant “tangential” velocity and no “radial” velocity. Just as the velocity of the fluid elements in the steady wind can be represented by vec­tor arrows, the same can be done for the fluid elements in the vortex. In this case the arrow is a line whose length is proportional to the speed but whose direction always lies along a tangent to the circular streamline. The direction of the tangent varies as the fluid element proceeds around the streamline, although its length stays the same. Figure 4.1 shows a vortex with a clockwise rotation and gives the arrows of speed and direction at two important posi­tions. At what may be called the six o’clock position the arrows are horizontal and facing into the steady wind, while at the twelve o’clock position they are horizontal but point in the same direction as the uniform wind.

Typically one further important assumption was made about the struc­ture of the simple vortex. It was specified that the fluid elements that circle

around the vortex near the center move along their assigned path with greater speed than do fluid elements circling at a greater distance from the center. The speed drops off uniformly with distance from the center. The greater the radius of the streamline, the smaller the tangential velocity. The assumed relation can be expressed more precisely by saying that, for the kind of simple vortex under consideration, the speed of the flow (v) at any given point is “inversely proportional” to the radius (r) of the circular streamline that runs through that point. In mathematical terms the formula relating speed and radius is then v = k/r, where k is the constant of proportionality.

Now imagine that the constant wind and the vortex are superimposed. The two flows, which have hitherto been treated as separate cases, are now combined. What is the result? In reality, the mixing together of two flows, whether in water or air, is accompanied by all manner of eddying and tur­bulence produced by viscosity and other physical features of the fluid. In the analysis developed for aerodynamic purposes, all of these complications were put aside and an extremely simple process of combination was assumed to provide an adequate description. Because the two flows that are combined are steady, the new flow will also be steady and all that was necessary to describe it was a process called vector addition (see fig. 4.2).

R

RESULTANT VELOCITY

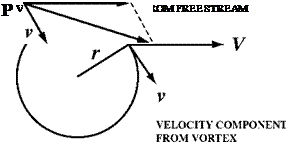
figure 4.2. At each point P in the combined flow of a steady wind and a vortex, two components are combined and determine the velocity of the resultant flow (a). This is done through vector addition, as shown in (b), which involves completing the parallelogram of velocities to give the speed and direction of the resultant velocity.

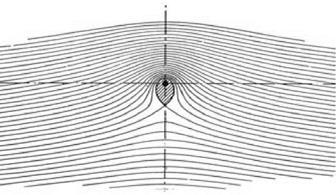
figure 4.3. The flow that results from the combination of a uniform free stream and a vortex. The streamlines above the center of the vortex are closer together than below it, showing that above the vortex the speed is higher, and the pressure lower, than below the vortex. There will be a resultant force directed upward, that is, a lift force. From Lanchester 1907, 164.

At any given point P in the new flow, there are two vector arrows to take into consideration. One, provided by the steady wind, is horizontal; the other, provided by the vortex, is at an angle determined by the position of P relative to the center of the vortex. P is located at some radial distance from the center of the vortex (this determines the speed), while the direction of the vortex component is determined by the direction of the tangent of the streamline that passes through P. A typical case is shown in figure 4.2a. The procedure needed to combine the effects of the two flows is shown in figure 4.2b. The resultant velocity is given by a geometrical construction called “completing the parallelogram,” whose intuitive meaning can be read directly off the diagram. Completing the parallelogram gives the speed and direction of the new flow at that point. A picture of the combined flow can be built up by the carrying out of this process at a large number of points. It will have the general appearance of figure 4.3, which is taken from Lanchester’s Aerodynamics.

The diagram shows that the streamlines are closer together above the cen­ter of the vortex than below, and this difference indicates a speed difference. The speed of flow above the vortex is greater than the speed below. How does this arise? To explain this occurrence it is sufficient to focus on two particu­larly important positions in the vortex, namely, the twelve o’clock and six o’clock positions, which are directly above and directly below the center of the vortex. Here the vector addition effectively reduces to simple arithmetical addition because there is no angle between the contributions of the two flows. At both points, but only at these points, the effect of the vortex is exactly aligned with the horizontal wind. At a point positioned some given distance r directly above the center of the vortex, the speeds of the two flows are going to add together to produce a flow with the speed V + v. At a diametrically opposite point, a distance r directly below the center, the two flows will op­pose one another to produce a reduced speed V – v. Elsewhere in the flow, at points not directly above or below the vortex, the contribution of the vortex component will augment the upper half of the flow, and diminish the lower half of the flow by less than v, but the general effect will still be present. Hence the spacing of the streamlines visible in Lanchester’s diagram.

The crucial step is the next one. The supporters of the circulatory theory supposed that, as it moves through the air, an aircraft wing (viewed in cross section) somehow generates a vortex effect around itself. There is, they ar­gued, a vortex “bound” to the position of the wing. The effect of the wing is to be represented by a vortex, even though the wing profile has an elongated shape, while the vortex is circular in form and centered on a geometrical point. Why a wing has this effect on the air and why it can be represented in this way were problems for the supporters of the theory, but they proceeded on the assumption that this was the case. They accepted that near the wing the flow could not look exactly like a combination of a steady wind and a vortex but that the picture became more accurate at a distance. Following the reasoning set out here, and applying it to the case of the wing, they argued that if the flow around the wing consisted (approximately) of a uniform flow combined with a vortex, then some of the air at a given distance above the wing would reach a maximum speed of V + v and some of the air at the same distance below it would drop to the speed V – v. Here was an explanation of the required speed differential in the flow over the wing, which in turn ac­counted for the pressure differential, and thus for the lift. Or, to be more pre­cise, here was an explanation of lift if the assumption is granted that the wing generates a vortex. But should this point be granted? The question epitomizes all the subsequent arguments over the circulatory theory.

Does the circulation theory imply that, during normal flight, molecules of air make a journey around the chord of the wing? No, this is not what its supporters were saying. Such a picture may be conjured up by abbreviated formulations, such as “lift is created by the circulation of air around a wing,” but these words depend on a technical meaning of the word “circulation” and do not mean what they may seem to mean. It is true that in an isolated vortex, such as a whirlwind, the air does indeed make a circular journey around the center of the vortex, but the theory does not require this to happen in the case of a wing delivering lift. The actual flow involves fluid elements curving up slightly to meet the leading edge of the wing. They then travel along the chord of the wing and leave with a slight downward inclination of the streamlines at the trailing edge. The claim is merely that during normal flight, the vortex exists as a component of this overall flow pattern.

In 1903 the Cambridge logician Bertrand Russell argued that “the compo­nent of any. . . vector sum, is not part of the resultant, which alone could be supposed to exist.”5 Russell (who was seventh wrangler in 1893) did not have aerodynamics in mind but was writing about the nature of mathematical con­cepts in general. His position suggests that only the resultant flow of air over a wing really exists, whereas the uniform flow and the vortex, being mere com­ponents, do not really exist. Such a conclusion does not do justice to what the supporters of the circulatory theory were saying. The component flows were meant to describe real tendencies existing in the resultant flow. These tendencies can be “supposed to exist” even when not manifesting themselves in isolation from other tendencies. This realistic way of speaking seems more natural than Russell’s formulation and better covers the range of empirical possibilities that would have been evident to those working in aerodynamics. First, the realistic idiom implies that if one contrived to bring a moving (and lift-generating) wing to a sudden halt in midair, then the circulating tendency would have nothing to modify it and would reveal itself in its full form.6 In these circumstances there would be air swirling around the wing. Second, as a general fact about vortex flow, if a very strong vortex is combined with a uniform wind, some of the air close to the center of the vortex actually will go around in a closed loop. (An examination of Lanchester’s diagram in fig. 4.3 shows that it represents a flow of this kind.) These considerations suggest that Russell was wrong and that the components of the vector addition can be as real as the resultant. Whether these real tendencies display themselves as independent phenomena is merely a matter of how strong they are relative to the other components.