Category The Enigma of. the Aerofoil

Now it was time to compare the theoretical predictions with the results of ex­periment. Kutta did not perform experiments himself but used existing data. The aim was to see if the predicted relation between lift and angle of incidence was correct. The formula for the circulation shows that the circulation increases with increasing angle of incidence, so lift should likewise grow. Kutta worked out two sets of testable results, one for a flat plate, the other for the curved wing. The two predictions are closely related because the flat plate is just the limiting case of the curved plate. The limiting process greatly simplified the formula and permitted a rough comparison with flat-plate data already pub­lished by Duchemin and Langley. The experimental lift was about two-thirds of that predicted by the theory. Kutta declared this “nicht ganz schlecht” (52), which might be rendered as “not too bad.” In his discussion of the flat plate, Kutta also established that the center of pressure will be at a point one-quarter the width of the chord from the leading edge and that, unlike for the curved plate, the position stays the same even though the angle of incidence changes.

Coming now to the curved wing, Kutta used Lilienthal’s own data, which were generated by experiments on a small model of an arc-shaped wing with a sharp leading edge. Because of the sharp leading edge, Kutta thought that friction effects would be dominant so that the leading-edge suction would be damped down or removed. He therefore compared Lilienthal’s measurements with predictions drawn from two different parts of the theoretical analysis. In one case he computed the lift from the general formula showing that the lift = density X velocity X circulation. In the other he used the pressure lift alone (that is, the theoretical lift minus the leading-edge suction). This latter case created a drag because the resultant was tilted backward. On the basis of cer­tain assumptions about the test conditions, Kutta made his predictions for lift and drag for nine different angles of incidence from -9°, through 0°, to +15°. Overall he found that the theoretical predictions of lift were consistently 10 -20 percent higher than those arrived at by observation. Kutta concluded:

Aus der Tabelle scheint also hervorzugehen, dafi fur die untersuchte gewolbte Flache und fur Luftstofiwinkel unter 15° die beobachtete Hubkraft 80-90 Prozent der errechneten ausmacht—was mit dem Umstande, dafi die theore – tischen Vereinfachungen sicher auf zu grofie Zahlen fuhren mufiten, in Uber- einstimmung steht. Auch fur den Stirnwiderstand ergeben sich einigermafien brauchbare Zahlen. (54)

It follows from the table that, for the curved surfaces that were studied, the observed lift force was 80 -90 percent of the calculated value for angles of incidence below 15°—which constitutes agreement given that the theoretical simplifications were bound to lead to numbers that were too high. Even the values for the frontal resistance are reasonably useful.

In other words, the theory fitted the data tolerably well given the approxima­tions that had been made.

Prandtl took a significant step toward greater realism when he went be­yond the idealization of the infinite wing. But, as von Mises emphasized, Prandtl’s own work rested on numerous idealizations. Prandtl was fully aware of this. He explained, for example, that the lift force was assumed to be small so that changes in the direction of the airflow would also be small. Mathematically this justified the neglect of all but the lowest order of the quantities under consideration and made the theory linear. As we have seen, the wing was replaced by a bound vortex, a lifting line, and was treated as if it had no chord. Central to the process of idealization was the now familiar horseshoe vortex. The metaphor of the horseshoe is strained be­cause the vortices in Prandtl’s model were in the form of straight lines with right-angled bends, whereas horseshoes are curved. How did the schemati – zation acquire this inappropriate name? The answer links together some of the sparse facts about the relation between Prandtl’s work and Lanchester’s book. It also provides material for reflecting more generally on the role played by idealization.

In Lanchester’s Aerodynamics there is a drawing of the vortex system around, and behind, a wing (175). Lanchester’s sketch is reproduced here as my figure 7.14. The likeness is not exact, but Lanchester drew the vortices in a way that looked roughly like a horseshoe. They are certainly much more horseshoe-like than the vortex system made up of the three straight lines that Prandtl used. Although Lanchester himself called the shape a “hoop or half­ring” (174), this description must have been the origin of the “horseshoe” metaphor. The Hufeisen label presumably arose in Gottingen as a natural response to Lanchester’s truly horseshoe-like figure.

Prandtl knew Lanchester’s book, and he knew Lanchester’s drawing. He mentioned it explicitly in one of the few reflective pieces he wrote

about his methods of work. In a talk he gave in 1948, called “Mein Weg zu hydrodynamischen Theorien” (My route to hydrodynamic theory), he re­marked that it was frequently his doubts about existing treatments of a prob­lem that spurred him to new ideas—and he instanced this particular diagram in Lanchester’s book as an example.84 Unfortunately, he did not specify exactly what it was about the figure that struck a discordant note. A probable answer is that the figure looked wrong because Prandtl took it to be a consequence of Helmholtz’s theorems that the trailing vortices would be carried along by the streamlines and, to a first approximation, these would be the straight stream­lines of the free flow. The free-vortex lines would not coincide exactly with a prolongation of the original, straight streamlines (because they would have a slight downward movement), but they would not have the marked, outward curving, horseshoe-like shape attributed to them by Lanchester.85 The defect in Lanchester’s figure was removed in the better, though still approximate, straight-line diagram that Prandtl subsequently used. This showed the trail­ing vortices going straight back from the wingtips.

Was the error in Lanchester’s figure obvious to Prandtl the moment he set eyes on the original diagram, or did it take some time before the problem emerged into view? There are grounds for thinking that the error may not have been immediately obvious. The horseshoe-like diagram was not modi­fied in the German translation of Lanchester’s book made in 1909 by Prandtl’s friends Carl Runge and his wife. Had the diagram seemed obviously wrong from the outset, Prandtl would have mentioned it to his friends, and the mat­ter would have then been raised with Lanchester in the discussions that took place in Gottingen over the translation. The opportunity would have been taken to modify the text in the same way that an opportunity was taken to add a mention of Prandtl’s 1904 boundary-layer paper.

Although Prandtl introduced his quantitative theory in 1910, in the sum­mer semester of 1909 he had already given a series of lectures on the scientific basis of airship flight in which, in addition, he had touched, qualitatively, on the circulation round the finite wing of an aircraft. Some of Otto Fop – pl’s notes of those earlier lectures have survived and are reproduced in Ju­lius Rotta’s beautifully illustrated book Die Aerodynamische Versuchsanstalt in Gottingen.86 Foppl’s lecture notes include a diagram that he presumably copied from one of Prandtl’s own blackboard drawings. The diagram shows the vortices curving out from the wingtips in the way Lanchester had origi­nally presented them. It seems that in 1909 Prandtl had drawn the vortex sys­tem so that it did indeed still look like a real horseshoe. Foppl’s diagram also contains a cross section of the trailing vortices that clearly shows the core of the vortices separated by a distance considerably greater than the wingspan, thus confirming the idea that the vortex lines were not meant to go straight back from the tips. The mere presence of the diagram does not prove that Prandtl had drawn it on the board as an example of truth rather than error, but a probable sequence of events would be this: Prandtl started by accept­ing the (curved) horseshoe picture, as did Finsterwalder, but within a year realized that it was wrong. Henceforth his model had straight lines. Despite this change of mind, the name Hufeisen appears to have stuck and was used, somewhat incongruously, for the simple, straight-line vortex schema that re­placed the original curved horseshoe.87

I shall now comment on the important transition from the simple, straight-line horseshoe schema to the refined version involving an infinite number of infinitesimal horseshoe vortices. The infinity of vortices coming away from the trailing edge creates a “vortex sheet” spread across, and trail­ing behind, the span of the wing. In the simple schema there was a vortex line coming from each tip; now there is something like a continuous train of vor – ticity attached to the rear of the wing. This changes the picture considerably. It also poses a problem. If this picture is right, the earlier picture was wrong, but the supporters of the circulatory theory claimed to have actually seen the simple horseshoe structure. In the first publication to use Prandtl’s theory, Foppl said that the two vortices trailing from the wingtips had been made visible in the wind channel by introducing ammonia vapor. Nor was it just the members of the Gottingen group who claimed to have seen the horse­shoe-like vortices. A similar, though more guarded, claim had been made by Lanchester, who had moved a model aerofoil under water and claimed to have “traced experimentally” the vortices that were postulated in his theory.88 But if these two trailing vortices are now discarded as theoretical fictions, what was it that had been made visible? One possible answer, according to later versions of the theory, was that the phenomenon reported was really

the rolling up of the vortex sheet. Prandtl argued that the sheet was unstable and rolled up at the edges in the way shown in figure 7.15. The rolled-up sheet then decayed into something resembling the two trailing line vortices. Per­haps this is what had been seen.89

There remains a further and deeper question about the move from the single, horseshoe vortex to the infinite number of trailing vortices that now constitute the vortex sheet. I have explained that the single, horseshoe schema could not do justice to what was known experimentally about the distribution of lift along a wing. Greater realism required a non-uniform lift distribution across the span, with zero lift at the tips. Accordingly, Prandtl replaced his single, highly abstract, horseshoe model with an infinite number of similar models. No fundamental principle of the original model was changed in the course of producing the more refined version. In fact, those principles were reproduced an infinite number of times. Can this be right? Can an unrealistic construct be made more realistic by repetition? The refined horseshoe model shows that the answer to this question must be yes.

The earlier discussion of Prandtl’s boundary-layer theory showed that the realism of a theory may be increased even though physically impossible ide­alizations were still present. Now the point can be taken further. Realism may be increased by increasing the number of idealizations. It may sound wrong to say that “realism” is increased, while attributing that increase to the in­creased use of highly “unreal” instruments of thought, such as ideal fluids and infinitesimal vortices, but the discomfiture must be overcome. The essential point is that there is no valid inference from the desirability of greater realism, as that word is normally understood, to the undesirability of idealization. If a theory has been made more realistic, it does not follow that abstractions and idealizations must have been removed or their number diminished. This might, on occasion, be part of the story, but the move to greater realism bears no necessary relation to a reduced number of abstractions and idealizations.

Prandtl and his colleagues were not inclined to be apologetic about the abstractions they deliberately introduced into their theory, nor were they in any doubt that they were grasping reality. As Prandtl insisted to his Ber­lin friend von Parseval, the Gottingen work on vortex theory was successful because of its abstractions, not in spite of them. In discussing a paper that von Parseval had given on the formation of vortices on a wing, Prandtl com­plimented von Parseval on his treatment but contrasted their approaches.90 He put it like this: “Herr Professor v. Parseval hat der Wirbeltheorie, die bei unseren eigenen Arbeiten immer etwas Abstraktes behalten hat (die allerdings gerade durch die bewufit eingefuhrten Abstraktionen zu ihren Erfolgen fuhren konnte), eine anschauliche Deutung gegeben” (63) (Prof. v. Parseval has given an intuitive significance to the theory of vorticity. In our own work it has always been treated rather abstractly [though it is, neverthe­less, precisely because of these consciously introduced abstractions that it has led to success]). Prandtl’s assistant Max Munk surely spoke for the Gottingen group as a whole when he insisted that the formulas of Prandtl’s wing theory represented “die wirkliche auftretenden Vorgange”—“the actual processes that occur.”91 The consciously introduced abstractions were the means by which the real and actuality occurring processes were described.

The stance of Prandtl and Munk, and the striking achievements of the Gottingen approach suggest a bold generalization. Perhaps successful work of this kind will always be based on idealizations and abstractions. If this is cor­rect, then what is really at issue is not whether abstractions are to be used but which abstractions are to be used. Which are to be counted as having a role in the laws of nature and which not? Scientists and engineers themselves, collec­tively, have the responsibility of according or withholding that status and of saying which abstractions and idealizations best describe the actual processes that occur in nature. Different groups may discharge this responsibility in dif­ferent ways. This fact has already been encountered in the different positions adopted by British and German experts with regard to the Stokes equations. Now we have another example. For the German aerodynamic community, unlike the British, the pragmatic success of the circulatory theory of lift, even within a limited technological domain, was evidence enough that the gulf between thought and reality was being overcome.

What is the correct understanding of Taylor’s “Note on the Prandtl Theory” and the mathematical arguments he put forward? What might explain the in­version of its perceived significance? Why did Taylor himself begin that pro­cess when he reworked the conclusion to the original note in his published appendix? Clearly, Taylor was not trying to rehabilitate the old discontinuity theory; he was merely using it to embarrass the supporters of Lanchester and Prandtl. He was showing that there was no unique explanation of the phe­nomena summarized by the Kutta-Joukowsky law.22 Taylor can therefore be seen, at least initially, as putting forward counterexamples in order to make a logical point. He was concerned with what follows, or does not follow, from the standard formulation of the circulation theory of lift. He had caught Glauert out in a hasty inference, but to show that proposition A does not

entail proposition B does not prove that B is false. Taylor’s argument did not establish the falsity of the conclusions that Glauert drew about the results that were emerging from Bryant and Williams’ experiment.

As well as measuring the circulation along contours that enclosed the wing, Bryant and Williams also measured the circulation around contours that did not enclose the wing. This part of their argument remained intact. They di­vided the space around the wing into zones, like tiles on a bathroom wall, and then measured the circulation around each zone (see fig. 9.4). The question they posed was the following: Were these local circulations all zero? Zero cir­culation was required for these contours (that is, contours not surrounding the wing) because that would indicate that the main flow was irrotational, namely, an irrotational motion but with circulation around the wing. Not all of these local circulations turned out to be zero. As can be seen in figure 9.4, there were a number of anomalous values particularly among those recorded near the leading edge. Despite this, enough of the readings were sufficiently close to zero for the measurements to be seen as a vindication of the theory. This result had emerged after Glauert’s preliminary analysis and after Taylor’s original note. It was therefore too late to have played any role in the exchange in the Aerodynamics Sub-Committee, but it was acknowledged in the pub­lished version of Taylor’s note attached to Bryant and Williams’ paper in the Philosophical Transactions.

The new data may have contributed, in some measure, to the change in Taylor’s tone between the unpublished and the published versions. Despite limitations in the experimental design, the overall picture that emerged from the experiment favored the circulation theory. Taylor therefore had little choice but to begin the published version of his comments by accepting that, after all, the flow was mainly irrotational. As he put it: “In their paper ‘An Investigation of the Flow of Air Round an Aerofoil of Infinite Span,’ Messrs. Bryant and Williams show that the flow round a certain model aerofoil placed in a wind channel is not very different from an irrotational flow with circula­tion. There are, however, differences which are considerable in the wake, a narrow region stretching out behind the aerofoil” (238).

The acknowledgment that the flow outside the wake was “not very differ­ent” from irrotational gave the supporters of the circulation theory all they really needed. Taylor had himself identified this as “Prandtl’s fundamental hypothesis,” but though he was now conceding the point he did not linger on the concession. Taylor immediately drew attention to the flow inside the wake, which was nonirrotational. This point was the real focus of his interest. The Aerodynamic Sub-Committee discussions of the preliminary data com­ing from Bryant and Williams, in December 1923, had charged Taylor with the task of differentiating “between the effect due to circulation and that due to eddying on the forces as measured on a complete aerofoil.”23 The “Note on the Prandtl Theory” was his response to this request. In the same spirit, when Bryant and Williams gave their technical report to the committee, Tay­lor drew attention to the apparent presence of local areas of significant circu­lation where there should have been none. Glauert, by contrast, wondered if this result could be an artifact produced by the compounding of small errors elsewhere in the data.24

In taking the line he did in his note, Taylor showed that his thinking fell into the familiar pattern that was characteristic of British work—with the exception of Glauert’s. Taylor’s counterexamples were an expression of the old argument that perfect fluid theory must be false because it predicted zero drag for an infinite wing. The wake was the physical source of the drag, and drawing attention to it and exploring the consequences of its presence, merely underlined the standard objection. If, along with a wake and a viscous drag, the Kutta-Joukowsky law of lift turned out to be approximately true of the flow, then some other reason had to be found to explain the law than the one originally advanced. In a real, viscous fluid, there was no well-defined quan­tity that could be called “the” circulation of the flow. The value of the relevant integral would not be contour-independent but would, in general, vary from contour to contour. This was why Taylor stressed the contour dependence of the experimental results. Taylor, however, was not asserting anything that the defenders of Prandtl’s theory had not granted long ago. In 1915 Betz had made a correction to allow for the role of the wake. There was no inconsistency between what Taylor said in the passage quoted earlier, in which he conceded the generally irrotational nature of the flow, and what Glauert had said origi­nally in his technical report “Aerofoil Theory,” in which he had conceded a viscous wake. Both men acknowledged the presence of rotational and irro- tational flow in the phenomenon before them. The difference between them lay in their reaction to this agreed fact. It was a difference of emphasis and preferred method. Taylor wanted to know where the inviscid approach failed, whereas Glauert wanted to know where it worked. Taylor’s eyes were directed to the viscous wake, whereas Glauert’s gaze was on the nonwake.

This concern with the wake may help explain the inversion that took place in the perception of Taylor’s argument, and even why Taylor himself reex­pressed his original, negative point in an oddly positive way. The ideas Taylor used, negatively, to construct the counterexamples to the circulation theory became resources that could be used, positively, to study the wake. This study rapidly became a subject of research in its own right. The ideas Taylor origi­nally advanced as counterexamples found a new use. Perhaps it was the tran­sition to this new role that gave rise to the later misunderstanding. The new studies of the wake did not displace the circulation theory of lift but came to complement it. The viscous flow inside the wake found a place alongside the inviscid flow outside the wake. Nor did the two merely coexist. Rather, the latter could be seen as the limiting case of the former. As the wing increases in efficiency, so the wake gets smaller. In the limit the wake is simply the vortex sheet behind the wing, which was central to Prandtl’s analysis. Taylor’s viscous, rotational wake becomes, to use Glauert’s word, “evanescent.” Un­derstood in terms of Glauert’s methodology, the reality of the wake was not being ignored but was allowed for in the limiting process by making the right choice of the inviscid flow. The counterexample then becomes identical with the phenomenon it was meant to contradict. Perhaps Glauert had begun to convince Taylor that the seeming contradiction between his counterexamples and the theory were not as logically sharp as it first appeared. Glauert would surely have discussed the problem with Taylor in the time between Taylor’s (unpublished) note and his (published) appendix. If minutes had been taken of these discussions, it might have been possible to trace the process by which Taylor came to reformulate his original doubts.

What is a matter of public record is how Taylor’s argument was deployed for the purpose of studying the wake. Recall that Taylor’s analysis of mo­mentum relations concerned not only lift but also drag. The physical basis of Taylor’s calculation of drag was the idea that drag arises from a loss of momentum in the fluid flow behind the obstacle. His analysis showed that this loss implied a pressure reduction in the wake, namely, a diminution of the quantity called the “total head” or the “total pressure.” (These terms were explained in chap. 2 in connection with Bernoulli’s theorem.) This account of drag was taken up by Fage and Jones at the National Physical Laboratory in a paper published in 1926 in the Proceedings of the Royal Society.25 They cited Taylor’s comments on Bryant and Williams’ work, but they did not read them negatively. They understood them as positive suggestions about the na­ture and measurement of drag and proceeded to do the experiments needed to test them. Bryant and Williams, they said, had explored the velocity of the flow in the wake of a model aerofoil spanning the wind tunnel and had shown that, for all practical purposes, it was two-dimensional. They went on: “In an Appendix to the above paper [by Bryant and Williams], Prof. G. I. Taylor shows that there is good reason to believe, on theoretical grounds, that the drag of an aerofoil can be determined with good accuracy from observa­tion of total-head losses in the wake, provided that these observations are taken in a region where the velocity disturbances are relatively small” (592). Fage explained that the drag under discussion was not Prandtl’s “induced drag,” which was a by-product of the lift, but “profile drag” associated with the shape and attitude of the wing section (592).

Fage and Jones’ experiment was to be carried out on an infinite wing with two-dimensional flow for which the induced drag should be zero. Using the symbol H to represent the total head ^p+1 pq2 j and, like Taylor, neglecting small quantities, Fage and Jones rewrote Taylor’s drag equation in a simpli­fied form as

D = pjH. ds,

C

where “the integration is taken along a line passing through the wake at right angles to the undisturbed wind direction” (594). Outside the wake, H will be constant from streamline to streamline but will vary as the line of integration passes through the wake. For a contour that cuts the wake parallel to the y – axis, the value of the direction cosine l is unity, which explains its apparent absence from Fage’s simplified expression. If Taylor’s analysis was right, the experimenter could measure the drag on a two-dimensional or infinite wing by summing up the losses in the total head across the span. This was what Fage and Jones did using a model wing of 0.5-foot chord mounted, with only a small clearance, right across the 4-foot wind tunnel. The wind speed was 60 feet per second. They calculated the drag from pressure measurements taken in the wake and performed the required integration using graphical methods. They found that most of the loss of total head pressure (H) came from a loss in velocity (q) rather than a reduction in the static pressure (p) of the wake. Finally they compared the predicted drag with the result of their di­rect drag measurements when the wing was suspended on wires and attached to scales. The two methods they concluded were “in close agreement” (593).

A further feature of Taylor’s argument that was given a new employment was his picture of the equal discharge of positive and negative vorticity into the wake (respectively from the upper and lower surfaces of the wing). This also helped to integrate the circulation theory into the study of viscous flow.26 The theorem that the circulation in all circuits enclosing the aerofoil had the same value, if the contour cut the wake at right angles, was, as one later re­searcher put it, “of fundamental importance in the calculations of the lift of aerofoils allowing for the boundary layer.”27 An important sequence of pa­pers starting in the mid-i930s was devoted to this theme, and they all traced their approach back to Taylor’s appendix. New ways were sought to general­ize the old Kutta condition in order to quantify the circulation under more complex and realistic conditions.28

As independent evidence in favor of some version of the circulation theory increased, the original significance of Taylor’s analysis, as a source of counterexamples, decreased. The ideas became consolidated in a new con­text. This may explain why von Karman and Burgers expressed themselves as they did. Perhaps they were not misreading Taylor so much as rereading him. That is, they were reinterpreting his original contribution in the light of later concerns and assimilating his ideas to the new preoccupations of a research agenda in which the circulatory theory of lift was taken for granted. Taylor’s line of thought was now being used to supplement rather than undermine the theory of circulation.

The British economy and the character of British culture provide the back­drop to the episode that I have been investigating. I now want to see how the British resistance to the theory of circulation fits into this broad picture. There are two, starkly opposed theories about the economic fortunes of Britain throughout the nineteenth and twentieth centuries and each carries with it a particular image of British society and British science. How does my story bear upon the dispute between the supporters of these two, opposing theories?

The first theory has been called declinism. The declinists hold that, after its initial lead in the industrial revolution, when the country was led by men who were “hard of mind and hard of will,” Britain ceased to be the workshop of the world and, ever since, has been in a steady state of decline both cultur­ally and economically. The main causes of the decline, the argument goes, are to be found in the antiscientific, antitechnological, and antimilitary in­clinations of subsequent generations of the British elite. The entrepreneurial spirit was drained out of British society, and innovation gave way to inertia. An important role in causing this sorry state of affairs is attributed to the universities. Universities are said to have cultivated the arts and humanities at the expense of science and technology. Literary and genteel inclinations were encouraged rather than more robust industrial and military values.34

The historian Correlli Barnett has formulated an influential version of the declinist theory in his book The Collapse of British Power.35 Barnett places great emphasis on national character. He diagnoses a fatal complacency that infected the British character after victory in the battle of Waterloo. Moral principle rather than self-interest became the dominant motive of political activity. Barnett is clear about the causes. The blame lies with the high-flown sentiments of evangelical religion and the ideology of individualism and free trade. Liberal economic doctrines, he concludes, were “catastrophically in­appropriate” for a Britain facing the growing economies of (protectionist) America and Prussia (98). By the 1860s, the misguided British faith in the “practical man,” along with the weakness of the educational system, had made the country dependent on its commercial and military rivals for much of its more advanced technology (96). By 1914 Britain, with its overextended empire, may have looked like a world power, but it was “a shambling giant too big for its strength” (90). In The Audit of War, Barnett acknowledges that the Cavendish Laboratory made Cambridge a “world centre of excellence” in science but insisted that this was “of little direct benefit to British industry.”36 The lack of industrial and commercial relevance was due to the cultural bias of the universities, particularly Oxford and Cambridge, against “technology and the vocational” (xiii): “Here amid the silent eloquence of grey Gothic walls and green sward, the sons of engineers, merchants and manufacturers were emasculated into gentlemen” (221).

Barnett acknowledges the success of the desperate, last-minute efforts that were made during the Great War to overcome the lethargy and inefficiency of British capitalism. In The Collapse of British Power he describes how the

Ministry of Munitions brought about a “wartime industrial revolution” (113) by setting up more than two hundred national factories for the manufacture of ball bearings, aircraft and aircraft engines, explosives, chemicals, gauges, tools, and optical instruments. But the effort was not to last, and the full lesson was not learnt. British economic performance and British power, he asserts, continued their trajectory of decline throughout the 1920s and 1930s. The defects of the British national character similarly bedeviled the coun­try’s struggle during World War II and, to Barnett’s evident disgust, expressed themselves after 1945 in the electorate’s desire to build a “New Jerusalem”—a welfare state.

This pessimistic picture has been widely accepted, but is it true? That it captures something is beyond doubt, but the basis of Barnett’s account has been challenged by the advocates of a rival picture. They may be called the antideclinists. Antideclinists acknowledge that there was an economic slow­down after 1870 but insist that if this counts as a “decline,” it was a relative, not an absolute, decline. It was almost inevitable as new nations industrial­ized and began to play a role in world trade. Thus in the early 1870s Britain produced 44 percent of the world’s steel, whereas by 1914 it produced 11 per­cent, but, as the economic historian Sidney Pollard put it, “It is evident that a small island with only limited resources of rather inferior ores could not go on forever producing almost half the world’s output of iron or steel; that share had to drop.”37

Pollard is by no means uncritical of British economic policy, but he takes the view that in 1914 the British economy was riding high. Decline, he sus­pects, is a political myth: “the statistics are against this argument.”38 With re­gard to the universities, antideclinists draw attention to the significant role of the British educational system in producing large numbers of scientists and technologists, many of whom have gone into government and industrial ser­vice.39 The declinists also tend to overlook the civic universities that emerged in the late nineteenth century and often worked in close conjunction with local industry.40

David Edgerton has presented the antideclinist case in a series of publica­tions that includes Science, Technology and British Industrial Decline, 1870­1970 and Warfare State Britain, 1920—1970.41 He argues that the declinist view rests on the claim that Britain has not spent enough on research and devel­opment (R&D). The declinist premise is that economic growth depends on R&D, but, says Edgerton, this premise is false: economic growth is largely in­dependent of investment in R&D. In any case, British spending on R&D has long been comparable to, or greater than, its competitors. Rather than being in the thrall of an antiscientific elite, Britain has been a scientific powerhouse during the twentieth century. Since 1901 Britain has won roughly the same number of Nobel Prizes as Germany. By 1929 well over half the students at British universities were studying science, technology, or medicine. In War­fare State Britain Edgerton notes that despite this, “The image of Germans as both militaristic and strong innovators and users of high technology in warfare is still a standard one in popular accounts” (274). It would be closer to the truth, Edgerton argues, to invert the usual stereotypes and apply this description to the British. British military policy has been to invest in the high technology of its navy and air force—and use them ruthlessly against the economy and civilian population of the enemy.

Edgerton has also marshaled the neglected evidence about the massive involvement of British scientists in governmental and military roles. The declinists ignore the historical, statistical, and economic data that support the view of Britain as a technological and militant nation. For Edgerton the declinist theory is not detached, historical scholarship; it is an ideology that expresses the partisan claims of a disgruntled political lobby. The unending complaint that British universities ignore technology and shun the scientific – military-industrial complex is actually the expression of an insatiable demand for ever more engagement. As Edgerton puts it: “I take the very ubiquity in the post-war years of the claim that Britain was an anti-militarist and anti­technological society. . . as evidence not of the theory put forward, but of the success (and power of) the militaristic and technocratic strands in British culture” (109).

How does my study fit into this debate? Does the British resistance to the circulation theory of lift provide evidence in favor of the declinist, or the antideclinist, view? At first glance it would seem to support declinism. I have identified an elite group of academically trained scientists who turned their backs on a workable, and technologically important, theory in aerodynamics. They left it to German engineers to develop the idea of circulation that had originated in Britain. This lapse seems to confirm the familiar, declinist story about the weaknesses of British culture. Rayleigh’s strengths lay in research rather than development, and as one commentator has put it, “Rayleigh’s weakness in this direction was an example of the British research and devel­opment effort in general.”42 The way Lanchester was sidelined surely epito­mizes the resistance to modernization. Putting aeronautics in the hands of a committee of Cambridge worthies and country-house grandees reveals the amateurism so characteristic of British culture.43

A closer examination of the episode casts doubt on this declinist read­ing. First, recall how closely the elite British scientists whom I have studied worked with the government and the military. From 1909 they were given a role close to the center of power, and they embraced it readily. The first place that Haldane went for advice, as the government minister responsible for military affairs, was Trinity College. The University of Cambridge provided the mathematical training of a significant number of Britain’s leading aero­dynamic experts, including Rayleigh, Glazebrook, Greenhill, Bryan, Taylor, Lamb, Southwell, and of course Glauert, who later championed the circu­latory theory. The intimate connection between academia and the military evident in the field of aerodynamics does not, in isolation, refute the declinist picture, but it certainly runs counter to it. It exemplifies the policy of high – technology militarism that has long characterized British culture but that is ignored by declinists.44

Second, the initial opposition to the circulatory theory must be put in context. The work of the Advisory Committee covered a broad range of other aerodynamic problems as well as lift. Along with the National Physical Labo­ratory and the Royal Aircraft Factory at Farnborough, the committee was deeply immersed in the theory of stability and control. We should not forget the words of Major Low, who recommended a comparative perspective. He argued that the British and the Germans both had their strengths and weak­nesses, and where one was strong, the other was weak. The British strength was stability.45 In this area the same group of experts who fell behind in the study of lift excelled and led the world. And they did this by using their Tripos, or Tripos-style, mathematics. In this case they did not call on fluid dynamics but on the equally venerable and equally abstract dynamics of rigid bodies. I have described the central role played in this area by the Cambridge-trained G. H. Bryan, who used the work of E. J. Routh, the great Tripos coach.

The conclusion must be that the same cultural and intellectual resources that had failed in the one case, the theory of lift, succeeded in the other, the theory of stability. British experts may have faltered over the theory of lift be­cause they were mathematical physicists rather than engineers, but it was not because they were effete or antimilitary or significantly antitechnological. Sta­bility is as much a technological problem as is lift. Nor did these experts falter over lift because they were torpid and unresponsive in the face of novelty and innovation. On the contrary, they rejected the circulatory theory of lift pre­cisely because it lacked novelty. It was novelty that the British experts wanted, not the old story of perfect fluids in potential motion. They were seeking in­novations in fluid dynamics and looking for new ways to address the Stokes equations. The theory of decline therefore points the analyst in precisely the wrong direction to appreciate the true nature of the British response.

The lesson to be learned is that broad-brush, pessimistic macro­explanations will not suffice. They do not fit the facts of the case I have studied.46 In Barnett’s words, British cultural life is identified as “stupid,” “le­thargic,” “unambitious,” and “unenterprising.”47 Some of it certainly is, but an unrelieved cultural pessimism can shed no light on the specific profile of success and failure that I have been analyzing. Declinist pessimism does not possess the resources to account for the successes of British aerodynamics that went along with the failures. In the event, it cannot even illuminate the failures themselves. Barnett’s contemptuous adjectives do no justice to the clever and ambitious British mathematicians and physicists whose work has been examined. His picture of pacifist tendencies hardly accords with the speed with which young Cambridge mathematicians volunteered for active service in 1914. What is needed, and what I have given, is a micro-sociological explanation that addresses both success and failure in a symmetrical manner. My account of the British resistance to the theory of circulation does not ap­peal to the vagaries of national character or broad, cultural trends. Like other studies related to the Strong Program, it rests on the technical details of the methods used by clearly identified scientific groups and the character of the institutions that sustained them.48

The administrative structure that crystallized in Haldane’s mind was for a committee of ten or eleven, involving persons of the highest scientific talent, to address technical problems presented to them by the Admiralty and War Office. Unlike the proposed committee itself, these two old-established bod­ies would be responsible for commissioning and even constructing military airships and aircraft. The committee would analyze and define the scientific and technical problems encountered by these constructive branches of the military and would pass them on to the National Physical Laboratory (the NPL). The laboratory, which was based at Teddington just outside London, was to have a new department specializing in aeronautical experiments. This department would produce the answers to the questions posed by the Advi­sory Committee. Financially, the committee would be accountable not to the War Office or Admiralty but to the Treasury.

The structure that emerged conformed to this plan except for the addition of one more unit. In 1911 the former Balloon Factory at Farnborough, be­longing to the army and the home of Dunne and his supporters, was turned into the Aircraft Factory and then (in 1912) into the Royal Aircraft Factory (the RAF).27 After the Dunne episode it had been decided to drop aircraft research at Farnborough, but this resolution was now rescinded. It was thus determined, after some indecision on Haldane’s part, that new aircraft were to be designed by the government itself and built at its behest by private manufacturers.28

An organizational chart of Haldane’s arrangement would therefore take the form shown in figure 1.2. Problems passed from left to right on the chart,

from the Admiralty and War Office through the ACA to the National Physical Laboratory and the Royal Aircraft Factory. After experiments and tests had been completed, according to a schedule agreed on with the ACA, informa­tion and answers were passed back, from right to left on the chart, in the form of confidential technical reports. After these were discussed and agreed on by the ACA, and any required amendments had been made, the outcome was to be published in the form of a numbered series called Reports and Memoranda—a series that, over the years, ran into thousands and was to become famous for its depth and scientific authority. Each year the Advisory Committee presented an annual report containing an overview of its activi­ties to which was attached, as a technical appendix, a selection of the more important Memoranda.

With the passage of time, and the increased workload imposed on the ACA, the original committee was broken down into a number of subcom­mittees to which further experts were recruited from the universities, Farn – borough, and Teddington. Thus there was an Aerodynamics Sub-Committee, an Accidents Sub-Committee, an Engine Sub-Committee, a Meteorological Sub-Committee, and so on. Sometimes the subcommittees were further bro­ken down into panels, such as the Fluid Motion Panel, which was part of the Aerodynamics Sub-Committee. Such a structure may seem complicated and bureaucratic, but viewed with the benefit of hindsight, it proved highly effective.

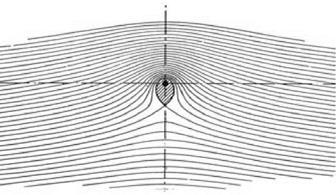
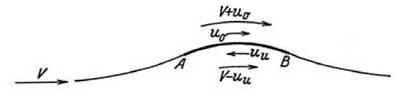
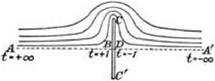
Although many flows were discovered by the indirect method, there are di­rect methods for describing a flow. How, for example, does the mathema­tician manage to describe the flow around a straight barrier that is placed facing head-on into a uniform stream of ideal fluid? The flow in question is sketched in figure 2.5, again taken from Cowley and Levy’s book. (Because the flow is presumed to be symmetrical around the central streamline of the main flow, only the upper half of the flow need be considered. The central streamline can be treated as if it were a solid boundary.) How can the equa­tions for the streamlines ever be discovered if the mathematician does not have the good fortune to come across a function amenable to after-the-fact interpretation? The answer is by cleverly establishing a relationship between

figure 2.5. Ideal fluid flowing irrotationally around a barrier normal to the free stream. From Cowley and Levy 1918, 49.

this complicated flow problem and the simplest of all possible flow problems, namely, the uniform flow along a straight boundary. The method involves transforming the straight boundary into the shape desired, for example, the shape of a barrier that is sticking out at right angles into the flow. The process is carried out by means of what is called a conformal transformation.

First, I should explain the word “transformation.” Everyone is familiar with the process of redrawing a diagram on a different scale. Suppose a geo­metrical figure has been drawn on one piece of graph paper, and it is required that the figure be redrawn, to a different scale, on another piece of graph pa­per. A line three centimeters long in the original is to be, say, six centimeters in the new diagram. A circle of radius four centimeters is to become a circle of radius eight centimeters, etc. The rule, in this case, is to double the length of the straight lines. The original diagram has thus been subject to a very simple, linear “transformation.” Other, much more complicated transformations are possible. Not only might a transformation magnify the figure in the original, but it might shift it relative to the origin, or rotate it or even distort it in vari­ous ways, turning, say, a circle into an ellipse. This shift will depend on the particular transformation that is being followed, namely, the particular rule that relates the positions of points in the one figure to the points in the other figure. If two figures are related by a transformation, then, if we know one of the figures, along with the rule of transformation, we can construct the other figure. A figure can be subject to more than one transformation so that a fig­ure which results from one transformation can be transformed yet again.

Transformations are important in hydrodynamics for the following rea­sons. First, the rules governing many transformations can be embodied in mathematical formulas that are functions of a complex variable. These are the conformal transformations. Second, if the flow around one shape is known, and a formula of this kind is available to transform the shape into a new shape, then the flow around the new shape is known. Conformal trans­formations change the streamlines as well as the boundaries of the figure, modifying the shape of the flow to fit the new circumstances. Methodologi­cally this is important. It means that, given an appropriate transformation, it is possible to move from simple flows, with simple boundaries, to the descrip­tion of complicated flows with complicated boundaries. All this can be done once it has been established that the transformation maps the boundaries of the two flows on to one another. Cowley and Levy sum up the situation, tersely, as follows: “It must be noticed that as long as complex functions are dealt with, the hydrodynamical equations will be satisfied and it will only be necessary therefore to consider boundaries. If a functional relation exist­ing between two planes is such as to provide a correspondence between the boundaries in these planes it is the transformation required” (47). The “two planes” referred to in this quotation are, in effect, just the two pieces of graph paper I mentioned at the outset. In this case, however, the idea is that one plane (usually called the w-plane) has the boundaries of a simple flow drawn on it, while the other plane has the, transformed, boundaries of the more complicated flow. This is usually called the z-plane and the transformation, or the sequence of transformations, links the two planes.

The problem is to find the necessary rule, or rules, of transformation. Fortunately there are general theorems that deal with the subject of transfor­mation which can be put to use. For example, there is a powerful result called the Schwarz-Christoffel theorem which proved central to classical hydrody­namics and, as we shall see in later chapters, also played an important role in the history of aerodynamics. The Schwarz-Christoffel theorem is applicable to the present problem, namely, finding the flow around a barrier across the flow of the kind shown in figure 2.5. This theorem, used by Cowley and Levy in their book, transforms the interior of a closed polygon on one plane (the z-plane) into the upper half of another plane (usually called the t-plane) and turns the boundary of the polygon into the real axis of the t-plane. If the t-plane can then be related to the basic, simple flow along the horizontal axis in the w-plane, then the requisite connections have been made. The simple flow with its simple boundaries can be turned into the complicated flow. The bridge is symbolized by w=f(z). Although the details need not be described, I want to sketch the way the theorem is used. The first step is to explain where, and why, polygons come into the story.

The polygon is familiar from school geometry and is usually defined as a many-sided figure whose sides are straight lines. A “closed” polygon obvi­ously has an inside and an outside. The exterior angles must add up to four right angles. The interior angles add up to (n – 2)n, where n is the number of vertices. Thus a rectangle is a simple case of a closed polygon that has just four vertices and in which each of the four interior angles is also equal to n/2.

The Schwarz-Christoffel theorem is embodied in the following, daunting, formula:

dz a-1 —-1

– = A(t-ti)n (t-t2)n…

dt

The letter A represents a constant and a, p, . . . are the internal angles of the polygon. The numbers fi, t2, . . . are real numbers ranging from minus infinity to plus infinity, with one number for each vertex. In order to put the formula to work to transform a given polygon, it is necessary to insert the values for the interior angles of the polygon, a, P, etc., into the formula and to assign the vertices of the polygon to the positions fi, t2, etc. on the real axis of the t-plane. (Some of these assignments can be made arbitrarily, while some de­pend on the shape of the polygon. In a moment I shall show how Cowley and Levy made the assignment.) Having filled in the appropriate values in the formula, we must then integrate it, and the result is a function of a complex variable z = f( t).

Why is this result useful when the aim is to find the flow around a barrier? The answer is that the complicated boundary, represented by the barrier in figure 2.5, can be counted as a closed polygon for the purposes of the theo­rem, and this fact can be exploited to get the desired flow. Given the picture of a polygon that comes to mind from school geometry, such a designation seems counterintuitive. The streamline along the axis of symmetry combined with the barrier normal to the flow doesn’t look like the polygons drawn on a school blackboard. Clearly, the words “polygon” and “closed” have been given a wider meaning. The justification is that the sides of a polygon can be made “infinitely long,” and the vertices dispatched to “infinity,” provided that the appropriate conventions are still kept in place regarding what counts as the interior and the exterior of the polygon. In this extended sense a poly­gon can even take on the appearance of, say, a single straight line.32 Crucially, it can also take on the appearance of the boundary in figure 2.5 that repre­sents a straight barrier jutting out into a fluid flow.

How is the diagram of the barrier-as-polygon connected to the Schwarz – Christoffel transformation formula? Look at Cowley and Levi’s figure, that is, my figure 2.5. The “vertices” of the “polygon” are marked A, B, C, D, A’. Inspection of the figure shows that A and A’ are both located at “infinity.” The points B and D are at the front and back of the base of the barrier, while C is at the top of the barrier. The “internal” angles can also be located. In moving along the boundary the point B is the location of a right-angle turn at the front of the barrier, while at C there is a turn through 180° at the top edge of the barrier, and there is another right-angle turn at D on the rear face of the barrier. These are the angles a, p, etc. to be inserted into the formula. Cowley and Levy’s diagram also shows how they have assigned t-values to these verti­ces. The one assignment not shown in the figure is the point C, the top of the barrier, which is given the value t = 0.

Once these particular values have been inserted into the formula it is ready to be integrated. After integration the constant A in the formula, as well as the constants of integration, can be evaluated by using the initial and boundary conditions of the problem. Proceeding in this way gave Cowley and Levy a formula connecting z and t, namely,

z = U] (t2 -1).

The process is, however, not quite finished. The basic, simple flow itself now needs to be expressed in terms of the t-plane. The t-plane is an intermediary between the z – and w-planes. Only when the t-plane has been linked to the w-plane will the desired connection have been made. The general form of the simple flow on the w-plane and the boundaries on the t-plane suggest that the link will be a simple one having two constants and taking the general form w = at + b. Consideration of the velocity of the flow at a great distance from the barrier, and the disposition of the bounding streamlines, allows the constants to be evaluated. The transformation connecting w and t is then given by the formula w = l V t, where V is the free-stream velocity and l is the half-length of the plate.

Combining the two formulas by eliminating t gives the result that has been sought, the complex function expressing the flow around the barrier. The desired formula is

f (z) = V^z2 +12.

Separating out the imaginary part, y, gives an expression for the streamlines of the flow, and from this the velocities and pressures on the boundary can be calculated. The formula for y turns out to be a complicated one, but it allows the curves to be drawn by setting y = constant. The formula is

y4 + V2(x2 – y2 + l2)y2 – V2x2y2 = o.

Now the streamlines of the flow of an ideal fluid around a flat barrier placed head-on to the flow can be calculated and represented with mathematical precision.

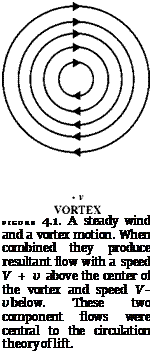
The remarkable fact that functions of a complex variable such as f(z) = (z + l/z) and f(z) = Vy/z2 +12 are all descriptions of irrotational flows has un­doubtedly left its mark on the development of classical hydrodynamics.33

It also raises a question. Why should the functions of a complex variable, containing esoteric mathematical entities such as the square root of nega­tive numbers, yield pictures of fluid flows? Consider the formula for the flow around a circular cylinder. The formula itself, f(x) = (z + 1/z), is not remark­able and is familiar to any student of mathematics (and we meet it again in a later chapter). It is hardly surprising that the formula is to be found in G. H. Hardy’s famous, Tripos-oriented textbook A Course of Pure Mathematics, first published in 1908. It crops up in the miscellaneous examples at the end of the chapter on complex numbers.34 But Hardy’s student reader was set the purely mathematical task of proving that (z + 1/z) transforms concentric circles into confocal ellipses. There was no mention of streamlines. The formula merely provided the occasion for an exercise in analytical geometry. That is what is puzzling. What has geometry got to do with fluids?

Part of the answer is provided by noticing that the functions that de­scribe the complicated flows do so by virtue of being transformations of the simplest possible flow, namely, the uniform flow of an infinite fluid along a smooth, straight barrier. But that merely pushes the problem back. Why should mathematics furnish a description of even the simplest of fluid flows, and why should that applicability survive the transformations leading to the complicated cases of flows that go around circular cylinders and encounter barriers? Does it all, perhaps, hint at a preestablished harmony between math­ematics and nature? Metaphysical responses of this kind have a long history. Famously, Galileo declared that God wrote the Book of Nature and did so in the language of geometry.35 Such reactions should not be dismissed. They represent an attempt to address a real question, and they are not confined to the past. Even contemporary physicists have been struck by the “unreason­able” effectiveness of mathematics in the natural sciences. The implication is that something beyond reason is at work, something mysterious and even miraculous.36 In the present case, however, any hint of the noumenal will be quickly dispersed when the empirical track record of the theory of ideal fluids is examined. I now turn to this side of the matter.

Within the framework of Newton’s mechanics, the flow of air around an air­craft wing can only support the weight of the aircraft if the flow generates a force that is equal and opposite to that of the weight. In level flight the upward force, the “lift,” must be in equilibrium with the downward force of gravity. Expressed in terms of fluid dynamics, the lift must be the result of air pressure on the wings. There must be an overall pressure imbalance between the upper and lower surfaces of the wing. The pressure of the moving air on the upper surface of the wing pushes downward. This must be surpassed by the pressure on the lower surface of the wing which pushes upward. It is the excess of the upward over the downward pressure that constitutes the lift and is therefore the central fact to be explained. It cannot be assumed that the resultant downward pressures and the resultant upward pressures act through the same point. In general they will not; the pressures on the wing will not only have the capacity to produce a lift, but they will also generate a turning moment that causes the wing to pitch. These pitching moments played a significant role in the analysis of stability carried out by G. H. Bryan. In what follows, however, I am mainly concerned with the resultant lifting effect of the pressures on the wing. I have already introduced Bernoulli’s law which implies that, if the air behaves like an ideal fluid, then the faster the air flows over the wing the lower will be the pressure it exerts, and the slower the flow the higher the pressure. If it is also accepted that the airflow around a wing is not discontinuous Rayleigh flow but follows the surfaces of the wing, then the problem of lift is simplified. It reduces to that of explaining why the air immediately below the wing is moving more slowly than the air immedi­ately above the wing.

Here it is necessary to avoid a popular misconception. A cross section of a typical wing has a flat base and a curved upper surface. The airflow di­vides at the leading edge, and some air takes the upper route over the curved surface while some takes the lower route along the flat and straight surface. Looking at such a shape, one can easily imagine two molecules of air parting company at the leading edge and joining up with one another again at the trailing edge. Like two travelers they wave farewell at the parting of the ways and then shake hands when they meet up later. But the low road is straight while the high road is circuitous, so the traveler who took the high road must have sped along more swiftly in order to meet up with the traveler who took the shorter path. Is this how it is with the air? Equal transit time plus a path difference certainly implies a speed difference, but this is not the secret of the wing.3 The questionable assumption is that the traveling companions, that is, the two molecules, meet up again. There are decisive reasons why this theory cannot be right. First, the increase in speed necessary to pass over the curved, upper surface of the wing would not generate the observed amount of lift. The path difference is not great enough. Second, the theory would have the conse­quence that an aircraft could not fly upside down. Once inverted, the curved surface would become the lower surface. The theory would then imply that the aerodynamic force would reinforce gravity rather than counteract it. But aircraft can fly upside down, so the theory cannot be right.4 This false theory, based on path difference and equal transit time, must not be confused with the circulation theory of lift. The circulation theory offers a very different account of the speed differences above and below a wing, as I shall now explain.

The flow of air over the cross section of a wing is a complicated phenom­enon, but, argued the supporters of the circulation theory, it can be thought of as built up out of two, simple flows. These are (1) a steady wind of constant speed and direction, and (2) a swirling vortex that goes round and round a central point. The two components are shown separately in figure 4.1. I dis­cuss each component flow in turn and then explore the flow that arises when they are superimposed on one another. The steady wind arises from suppos­ing a steady, relative motion of the wing and the air. In reality the air is sta­tionary and the wing moves, but, as previously noted, aerodynamic processes are frequently described in terms of the situation in a wind channel where it is the air that moves. Let the steady wind have a constant speed V and move horizontally. At any given point the flow can be represented by a vector, that is, an arrow pointing in the direction of the flow whose length is proportional to the speed. All the vector arrows representing the steady wind are therefore of the same length and can be assumed to lie horizontally, as shown in the figure. The streamlines of the flow are then equally spaced horizontal lines.

+ V

STEADY

WIND

The vortex flow is more complicated, but the early work on aerodynamics was confined to a particularly simple form of vortex. Let the vortex swirl in a clockwise direction around a central point that is assumed to be in a fixed po­sition. Unlike a normal vortex, in water or air, this one is not carried along by the stream. This special sort of vortex came to be called a “bound” vortex. All the streamlines in the vortex flow have the form of concentric circles. The fluid elements at any given distance from the center of the vortex are assumed to move with the same, constant speed around one of these circles. The elements do not get drawn into the center of the vortex. This is expressed by saying that they have a constant “tangential” velocity and no “radial” velocity. Just as the velocity of the fluid elements in the steady wind can be represented by vec­tor arrows, the same can be done for the fluid elements in the vortex. In this case the arrow is a line whose length is proportional to the speed but whose direction always lies along a tangent to the circular streamline. The direction of the tangent varies as the fluid element proceeds around the streamline, although its length stays the same. Figure 4.1 shows a vortex with a clockwise rotation and gives the arrows of speed and direction at two important posi­tions. At what may be called the six o’clock position the arrows are horizontal and facing into the steady wind, while at the twelve o’clock position they are horizontal but point in the same direction as the uniform wind.

Typically one further important assumption was made about the struc­ture of the simple vortex. It was specified that the fluid elements that circle

around the vortex near the center move along their assigned path with greater speed than do fluid elements circling at a greater distance from the center. The speed drops off uniformly with distance from the center. The greater the radius of the streamline, the smaller the tangential velocity. The assumed relation can be expressed more precisely by saying that, for the kind of simple vortex under consideration, the speed of the flow (v) at any given point is “inversely proportional” to the radius (r) of the circular streamline that runs through that point. In mathematical terms the formula relating speed and radius is then v = k/r, where k is the constant of proportionality.

Now imagine that the constant wind and the vortex are superimposed. The two flows, which have hitherto been treated as separate cases, are now combined. What is the result? In reality, the mixing together of two flows, whether in water or air, is accompanied by all manner of eddying and tur­bulence produced by viscosity and other physical features of the fluid. In the analysis developed for aerodynamic purposes, all of these complications were put aside and an extremely simple process of combination was assumed to provide an adequate description. Because the two flows that are combined are steady, the new flow will also be steady and all that was necessary to describe it was a process called vector addition (see fig. 4.2).

R

RESULTANT VELOCITY

figure 4.2. At each point P in the combined flow of a steady wind and a vortex, two components are combined and determine the velocity of the resultant flow (a). This is done through vector addition, as shown in (b), which involves completing the parallelogram of velocities to give the speed and direction of the resultant velocity.

At any given point P in the new flow, there are two vector arrows to take into consideration. One, provided by the steady wind, is horizontal; the other, provided by the vortex, is at an angle determined by the position of P relative to the center of the vortex. P is located at some radial distance from the center of the vortex (this determines the speed), while the direction of the vortex component is determined by the direction of the tangent of the streamline that passes through P. A typical case is shown in figure 4.2a. The procedure needed to combine the effects of the two flows is shown in figure 4.2b. The resultant velocity is given by a geometrical construction called “completing the parallelogram,” whose intuitive meaning can be read directly off the diagram. Completing the parallelogram gives the speed and direction of the new flow at that point. A picture of the combined flow can be built up by the carrying out of this process at a large number of points. It will have the general appearance of figure 4.3, which is taken from Lanchester’s Aerodynamics.

The diagram shows that the streamlines are closer together above the cen­ter of the vortex than below, and this difference indicates a speed difference. The speed of flow above the vortex is greater than the speed below. How does this arise? To explain this occurrence it is sufficient to focus on two particu­larly important positions in the vortex, namely, the twelve o’clock and six o’clock positions, which are directly above and directly below the center of the vortex. Here the vector addition effectively reduces to simple arithmetical addition because there is no angle between the contributions of the two flows. At both points, but only at these points, the effect of the vortex is exactly aligned with the horizontal wind. At a point positioned some given distance r directly above the center of the vortex, the speeds of the two flows are going to add together to produce a flow with the speed V + v. At a diametrically opposite point, a distance r directly below the center, the two flows will op­pose one another to produce a reduced speed V – v. Elsewhere in the flow, at points not directly above or below the vortex, the contribution of the vortex component will augment the upper half of the flow, and diminish the lower half of the flow by less than v, but the general effect will still be present. Hence the spacing of the streamlines visible in Lanchester’s diagram.

The crucial step is the next one. The supporters of the circulatory theory supposed that, as it moves through the air, an aircraft wing (viewed in cross section) somehow generates a vortex effect around itself. There is, they ar­gued, a vortex “bound” to the position of the wing. The effect of the wing is to be represented by a vortex, even though the wing profile has an elongated shape, while the vortex is circular in form and centered on a geometrical point. Why a wing has this effect on the air and why it can be represented in this way were problems for the supporters of the theory, but they proceeded on the assumption that this was the case. They accepted that near the wing the flow could not look exactly like a combination of a steady wind and a vortex but that the picture became more accurate at a distance. Following the reasoning set out here, and applying it to the case of the wing, they argued that if the flow around the wing consisted (approximately) of a uniform flow combined with a vortex, then some of the air at a given distance above the wing would reach a maximum speed of V + v and some of the air at the same distance below it would drop to the speed V – v. Here was an explanation of the required speed differential in the flow over the wing, which in turn ac­counted for the pressure differential, and thus for the lift. Or, to be more pre­cise, here was an explanation of lift if the assumption is granted that the wing generates a vortex. But should this point be granted? The question epitomizes all the subsequent arguments over the circulatory theory.

Does the circulation theory imply that, during normal flight, molecules of air make a journey around the chord of the wing? No, this is not what its supporters were saying. Such a picture may be conjured up by abbreviated formulations, such as “lift is created by the circulation of air around a wing,” but these words depend on a technical meaning of the word “circulation” and do not mean what they may seem to mean. It is true that in an isolated vortex, such as a whirlwind, the air does indeed make a circular journey around the center of the vortex, but the theory does not require this to happen in the case of a wing delivering lift. The actual flow involves fluid elements curving up slightly to meet the leading edge of the wing. They then travel along the chord of the wing and leave with a slight downward inclination of the streamlines at the trailing edge. The claim is merely that during normal flight, the vortex exists as a component of this overall flow pattern.

In 1903 the Cambridge logician Bertrand Russell argued that “the compo­nent of any. . . vector sum, is not part of the resultant, which alone could be supposed to exist.”5 Russell (who was seventh wrangler in 1893) did not have aerodynamics in mind but was writing about the nature of mathematical con­cepts in general. His position suggests that only the resultant flow of air over a wing really exists, whereas the uniform flow and the vortex, being mere com­ponents, do not really exist. Such a conclusion does not do justice to what the supporters of the circulatory theory were saying. The component flows were meant to describe real tendencies existing in the resultant flow. These tendencies can be “supposed to exist” even when not manifesting themselves in isolation from other tendencies. This realistic way of speaking seems more natural than Russell’s formulation and better covers the range of empirical possibilities that would have been evident to those working in aerodynamics. First, the realistic idiom implies that if one contrived to bring a moving (and lift-generating) wing to a sudden halt in midair, then the circulating tendency would have nothing to modify it and would reveal itself in its full form.6 In these circumstances there would be air swirling around the wing. Second, as a general fact about vortex flow, if a very strong vortex is combined with a uniform wind, some of the air close to the center of the vortex actually will go around in a closed loop. (An examination of Lanchester’s diagram in fig. 4.3 shows that it represents a flow of this kind.) These considerations suggest that Russell was wrong and that the components of the vector addition can be as real as the resultant. Whether these real tendencies display themselves as independent phenomena is merely a matter of how strong they are relative to the other components.

Two characteristics have now been identified in the British response to the circulation theory of lift. First, there was a desire for theories of wide scope that embrace complex viscous phenomena beyond the reach of the theory. Second, there was a tendency to read Lanchester as contributing to an inviscid theory and therefore as committed to a simplified and unreal representation of fluid flow. Both of these indicate the importance that British experts at­tached to the distinction between real fluids and ideal fluids. Taylor insisted that fluid mechanics should have a firm basis in physics and dismissed the idealizations of classical hydrodynamics. Cowley and Levy described inviscid theory as fatally flawed and spoke of the need for a theory of viscous flow that would solve the problems of aerodynamics at a stroke. Bairstow agreed that it was fundamentally impossible to represent real fluids in terms of ideal fluids and duly turned to the study of viscous flow. What Bairstow had asserted with characteristic acerbity, Lamb had hinted at with characteristic restraint. The different objections and formulations all point to one conclusion. The distinction between viscous and inviscid fluids is to be seen as the axis around which British thinking revolved.16

It is important not to view this distinction as self-evident or something that was understood in the same way by all competent operators in the field of fluid dynamics. In reality it was treated differently in different institutional settings. How then should the distinction between viscous and inviscid fluids be understood? Formally, it centers on whether p, the symbol for viscosity in the Stokes equations, is to have a value of zero or of nonzero. Was p = 0, or p Ф 0? Logically it must be one or the other and it can’t be both. Empiri­cally, whether Stokes’ equations turn out to be true, and Euler’s false, (or vice versa), is something to be settled by reference to experiment. But these tru­isms do not tell us how to interpret the difference between putting p = 0 or p Ф 0; nor do they indicate what physical meaning is to be given to the mathematical limit when p ^ 0. They do not tell us whether the distinctions involved are qualitative or quantitative or whether the boundaries under dis­cussion are strong or weak or for what purposes they might be important or unimportant. This is the point. The conceptual boundary between viscous and inviscid fluids is more than merely formal. Rehearsing the elementary mathematical properties of the distinction does not tell us what methodologi­cal implications are attached to it by the scientists concerned. I shall now illustrate the broader, methodological significance of the distinction by refer­ence to Lamb’s own discussion of viscosity.

Lamb began his account of aerodynamics, in the 1916 edition, by point­ing out that the analysis of Kirchhoff-Rayleigh flow was the first attempt, “on exact theoretical lines,” to overcome the result that a perfect fluid exerts no resultant force on a body. He added: “The absence of resistance, properly so called, in such cases is often referred to by continental writers as the ‘paradox of d’Alembert’” (664). Why did Lamb think that “absence of resistance” was the more proper description? What was wrong with talking about a “para­dox”? The reasoning behind Lamb’s remark went back to the first edition of his book, where he had originally addressed the well-known discrepancies between the empirical facts of hydraulics and the mathematical deductions of hydrodynamic theory. He traced the problem back to “the unreality of one or more of the fundamental assumptions” of the theory (244). The empirically false conclusion about resistance came from an empirically false premise, namely, the inviscid character of the postulated fluid. However, d’Alembert’s reasoning was sound, and the logic of the situation was clear. An inviscid fluid is correctly characterized by the absence of resistance. This is how ideal fluids behave or would behave. It is a simple fact about them, and there is nothing paradoxical about it.

A paradox is more than a falsehood, even a blatant falsehood. A paradox must involve a seeming contradiction. Suppose that experiments on a fluid F showed that it exerts a resultant force on a submerged body, while a mathe­matical analysis of F entails a zero resultant. Suppose, further, that the experi­ments on F seemed wholly reliable and the mathematical analysis of F seemed wholly correct. That would be paradoxical. Contradictory specifications of F have been generated from sources that seem undeniable. This is not the case if the experiments refer to a real fluid Fr, and the mathematics refers to an ideal fluid F. There is now no single point of reference as there was with the “paradoxical” fluid F. Two conditions are thus required to make d’Alembert’s result a genuine paradox: (1) there must be two plausible specifications that exclude one another, and (2) the two specifications must be applied to one and the same fluid.

Lamb avoided paradox by treating the two specifications as referring to different things. He drew a boundary between the referent of the experiment and the referent of the theory and thus rejected condition (2). In eschewing the word “paradox,” Lamb’s language was meant to carry a methodological message. It was a way of saying that viscous fluids were one thing and perfect fluids were another and never should the two be confused. This was an ad­mirably straightforward position, but was it the only tenable position? To ad­dress this question I consider a line of reasoning advanced by Ludwig Prandtl and Georg Fuhrmann in Gottingen. It will become clear that these experts did not distinguish between ideal and real fluids in precisely the same way as their British counterparts did.

Kutta ended with some ideas about extending his mathematical methods to a variety of different wing profiles with rounded leading edges and with flaps attached to the trailing edge. He mentioned the need to develop a more gen­eral form of the Schwarz-Christoffel theorem and indicated the demanding amount of computational effort that would be involved, but Kutta did not feel that the limits of his approach had been reached and hinted at their fur­ther application to biplanes.

Kutta’s next paper, in 1911, utilized the same mathematical techniques as those adopted in 1910 but it dealt with more complicated cases.33 The analysis was generalized in two ways. First, Kutta showed how to apply his conformal transformations to an aerofoil whose cross section was composed of not one but two circular arcs in the form of a crescent or sickle shape. Such a sickle­shaped profile was used in the successful Antoinette monoplane, and von Mises has suggested that its practical use was prompted by Kutta’s analysis.34 Second, Kutta generalized the approach in order to describe the flow over a number of wings that could be arranged to make a biplane or a triplane or even a multiwing arrangement in the form of a “Venetian blind.” Again, all of these forms had actually been used, or experimented with, by those who tried to build flying machines.

Having made these two outstanding contributions to aerodynamics, Kutta fell silent. He never published anything again. The reason for the silence is unknown.

The wartime activities of the Gottingen group, and their colleagues in the technische Hochschulen, proceeded on a much broader front than I have so far described.92 On the theoretical side, building on Betz’s early papers, there were studies by Betz, Munk, and Prandtl on the aerodynamics of biplanes and triplanes. Using the apparatus of the Biot-Savart law they produced some general theorems that helped to guide the aircraft designer through the maze of possible multiplane configurations. Betz had proven that, for an unstag­gered biplane, the induced drag effects of the wings on one another would be equal. For a staggered arrangement it was now shown that the sum of the mutually induced drags was constant and independent of stagger, provided that the lifts, and their distribution, were not changed. (This condition could be satisfied by changing the angle of attack.) In general, it was shown that the best biplane configuration was one with wings of equal length, with the up­per wing ahead of the lower. The biplane work also confirmed the important finding that elliptical lift distributions provided a good approximation for wings with non-elliptical planforms.93

On the empirical side, the war effort called for wind-channel studies of the drag generated by different aircraft components such as undercarriages and machine-gun mountings, engine-cooling systems, and the ubiquitous struts and bracing wires of the period.94 Work was also done on the lift and drag of the fuselage, the interaction between the fuselage and the wing, the effect of dividing the wing, the forces on fins and rudders, and the empirical properties of the triplane configuration.95 Experiments were done to test the resistance of the nose shapes required by different engine types, for example, rotary as compared with in-line engines, and attempts were made to add rotating propellers to the wind-channel models to achieve realism.96 Some wind-channel tests were also done on models of complete aircraft.97 Munk and Cario continued the studies initiated by Foppl of the downwash behind a wing. Whereas Foppl had worked with the overall force exerted by the down – wash on the elevator, Munk and Cario studied the downwash in much more empirical detail, using fine silk threads to trace the local variations. They un­covered significant complexities in the flow and made clear the need for a more extended program of work.98

Numerous studies were carried out to measure the lift and resistance of individual wing profiles. These were mainly overseen by Munk and his col­laborator Erich Huckel.99 Significant efforts were made to ensure that the re­sults were intelligible to those who might use them in practice.100 An attempt was also made to introduce order into the vast amount of data that had accu­mulated for different aerofoils, though the classification remained largely at the empirical level.101 One trend was toward an interest in thicker rather than thinner aerofoils, something that surprised the British when they examined captured German aircraft.102 An example of these thick aerofoils was the Got­tingen 298 used on the famous Fokker triplane. The use of the 298 profile by the designer Anthony Fokker does not, however, appear to have been a con­sequence of Prandtl’s recommendation or scientific knowledge of its good lift and drag characteristics (characteristics that, a priori and wrongly, the British designers doubted). In fact, the aerofoil was introduced into the Fokker pro­duction line by their chief engineer Reinhold Platz on the basis of trial-and – error knowledge. Later, and unknown to the people at Fokker, it was tested in Gottingen, where it was given its designation.103

The Fokker episode indicates that there was a continuing gap between the “practical men” of Germany and those self-consciously developing science- based procedures and working in academic and government institutions. The alienation of the practical men was not purely a British phenomenon, though it seems to have been less acute as a problem for German aviation than for British. Evidence in the technical reports indicates that the members of the Gottingen school were themselves aware of this gap and found it frustrating. Max Munk addressed the issue directly in a brief report of October 15, 1917, titled “Spannweite und Luftwiderstand” (Span and air resistance).104 Refer­ring to the practical conversion formulas linking wings of different aspect ratio, Munk complained:

Die kurzlich von Betz veroffentlichen Prandtlschen Flugelformeln werden wohl, da sie auf theoretischen Grundlagen beruhen, in der Praxis nicht so freundlich aufgenommen werden, wie sie verdienen. Das ist sehr schade, denn die Formeln enthalten mehr und leisten Besseres als der Praktiker geneigt ist, ihnen zuzutrauen. (199)

The formulas of Prandtl’s wing theory that Betz has recently published will probably not be welcomed in the realm of practice as much as they deserve because they rest on theoretical grounds. This is a great shame because the formulas offer more and give better service than the practical man is inclined to believe.

Munk went on to give an explanation of the significance of the formulas for the aircraft designer and some simple, general rules for the rapid calculation of the induced resistance and angle of incidence. Despite this evidence of skepticism in certain quarters, there was no shortage of contract work to be done for individual aircraft firms during the war years. This is attested by the frequency with which such names as AEG, Aviatik, Rumpler, Siemens and Schuckert, and Zeppelin were mentioned in the technical reports. Despite the problems of communication between the representatives of theory and practice, Prandtl’s institute had achieved a central position in what would now be called the military-industrial complex of Wilhelmine Germany. If this development brought frustrations as well as the advantages of government support, it is clear that striking progress had been made in aerodynamics, both empirically and theoretically.

One of the more unusual aerofoils whose properties were reported on by Munk and his colleagues was designated as profile 95. Visually it stood out from the usual run of aerofoil shapes (see fig. 7.16). The aerofoil looked like the back of a cat when the animal stretched, and it was duly given the nick­name Katzenbuckelflache. The Gottingen tests showed that the performance characteristics of the “cat’s-back” profile 95 were notably poor. It was tested by Max Munk and Carl Pohlhausen in the course of a run of work on nearly one hundred aerofoils. The results were listed together in the Technische Ber – ichte of August 1917 and showed that the maximum-lift coefficient for each wing in this sequence was typically in the region of 130 or 140. The maxi­mum lift coefficient for profile 95, by contrast, was given as 95.2. Again, the maximum lift-to-drag ratio was typically 14 or 15, while the ratio for profile 95 was 10.8.105 The designer of the cat’s-back wing was the celebrated physicist Albert Einstein.106 In retrospect Einstein felt that his excursion into aerody­namics had been irresponsible—he used the word Leichtsinn. From 1915 to

1917, Einstein had been a consultant to two aircraft firms, LVG and Merkur, and an aircraft had been equipped with the Einstein wing. The test pilot for LVG, Paul Ehrhardt, barely managed to get the machine off the ground and gave his professional opinion on the wing by saying that the airplane flew like a pregnant duck.107 The Gottingen tests made the same point in more scientific terminology.

No account remains of how Einstein actually designed the wing, but some insight into his thought processes may be gained from an article he published in 1916 in Die Naturwissenschaften. Here he set out to explain, in elemen­tary terms, the basic principles of lift.108 How does a wing support an air­craft and why can birds glide through the air? Einstein declared, “Uber diese Frage herrscht vielfach Unklarheit; ja ich mufi sogar gestehen, dafi ich ihrer einfachsten Beantwortung auch in der Fachliteratur nirgends begegnet bin” (400) (There is a lot of obscurity surrounding these questions. Indeed, I must confess that I have never encountered a simple answer to them even in the specialist literature). This is a striking claim, given that Einstein was writing a number of years after the publications of Kutta, Joukowsky, and Prandtl.

Einstein drew an analogy between the flow of fluid through a pipe of vari­able cross section and its flow around a wing. As fluid passes along a pipe that gets narrower, the fluid speeds up. By Bernoulli’s law the pressure will be lower in the fast, narrow section than in the broader section. Einstein then invited the reader to consider a body of incompressible fluid with no signifi­cant viscosity (that is, a perfect fluid) which flowed horizontally but where the flow was divided by a thin, rigid, dividing wall. The wall was aligned with the flow except that it also had a curved section where the wall bulged up­ward. (See fig. 7.17, which is taken from Einstein’s paper.) The curved section looks a bit like a cat’s back and would appear to have the same shape as the underside of the Einstein wing tested at Gottingen. Einstein argued that the fluid above the dividing wall will behave like the fluid in a pipe when it en­counters a narrowing of the pipe and will speed up and exert a diminished pressure on the wall. The fluid below the wall will behave like the fluid in a pipe when it encounters a widening out of the pipe so it will slow down and increase the pressure on the wall. The fluid pressure pushing upward on the curved section of the dividing wall will thus be in excess of the pressure push­ing downward, so there will be a resultant force upward All that is necessary now is to imagine that most of the dividing wall has been removed, leaving behind just the curved section. This procedure, argued Einstein, will retain the features of the flow that generate the pressure difference and hence will represent a wing with lift.

Einstein’s argument rested on the assumption that the removal of all but

the curved portion of the dividing wall would leave the flow unchanged at the leading and trailing edge of the remaining arc. He appeared to take this as ob­vious: “Um diese Kraft zu erzeugen, braucht offenbar nur ein so grofies Stuck der Wand realisiert zu werden, als zur Erzeugung der wirksamen Ausbiegung der Flussigkeitsstromung erforderlich ist” (510) (To generate this force it is obviously only necessary for part of the wall to be real. It need only be suf­ficiently large to produce the effective curvature of the flow). It is puzzling that Einstein made no mention of circulation. Was he aware of the circulation theory of lift? This remains unclear, but given that he assumed the air to be a perfect fluid, it makes it all the more important to ask how he proposed to circumvent d’Alembert’s paradox. How did Einstein expect to get a lift force rather than a zero resultant?

Although Einstein wrote in a dismissive way about the aerodynamic liter­ature, he had, in effect, taken the discussion back to where Kutta started it in 1902. When, following Einstein’s instructions, all of the wall dividing the flow is removed except for the curved piece, what is left is essentially Kutta’s arc at a zero angle of incidence. Einstein did not specify that the curve he discussed in his article was precisely the arc of a circle, but his argument was offered as a general one. If it were right it would apply to Kutta’s arc. But it does not. The arc is a counterexample to what seems to be Einstein’s argument, that is, to any argument that depends on ideal fluids but does not make provision for circulation. In order to generate lift, and to generate the requisite speed dif­ferential between the upper and lower surfaces of the arc, a circulation must be postulated. In a continuous perfect fluid flow, without an independently specified circulation, such an arc would not produce lift. D’Alembert’s para­dox would come into play. Such an arc would not have its stagnation points on the leading and trailing edge. The formula for the complex velocity has singular points indicating infinite velocities for the ends of the arc.109

In his diagram Einstein put the stagnation points on the leading and trail­ing edges of the arc even though he did not explicitly invoke a circulation. He put them where they would have been, given the appropriate amount of circulation needed to avoid infinite velocities at the edges. He did this by sup­posing that the guiding effect of the dividing wall, smoothly leading the fluid toward, around, and then away from the arc, would still be present even when the wall was removed and only the arc was left. There are no grounds for this assumption. Perhaps the best that can be said is that Einstein had, in fact, made provision for circulation in his analysis, but had done so tacitly and by questionable means. In his published lectures, a few years later, Prandtl gave a diagram that was almost identical to Einstein’s but, in Prandtl’s case, the com­ponent of circulation in the flow was properly identified and made explicit.110 Prandtl’s diagram is reproduced as figure 7.18 for purposes of comparison with Einstein’s figure.

It would seem that Einstein had little knowledge of current developments in the field of aerodynamics. This episode is a salutary reminder of the differ­ence between fundamental physics and technical mechanics. Eminence in the former does not guarantee competence in the latter.