Einstein’s Folly

The wartime activities of the Gottingen group, and their colleagues in the technische Hochschulen, proceeded on a much broader front than I have so far described.92 On the theoretical side, building on Betz’s early papers, there were studies by Betz, Munk, and Prandtl on the aerodynamics of biplanes and triplanes. Using the apparatus of the Biot-Savart law they produced some general theorems that helped to guide the aircraft designer through the maze of possible multiplane configurations. Betz had proven that, for an unstag­gered biplane, the induced drag effects of the wings on one another would be equal. For a staggered arrangement it was now shown that the sum of the mutually induced drags was constant and independent of stagger, provided that the lifts, and their distribution, were not changed. (This condition could be satisfied by changing the angle of attack.) In general, it was shown that the best biplane configuration was one with wings of equal length, with the up­per wing ahead of the lower. The biplane work also confirmed the important finding that elliptical lift distributions provided a good approximation for wings with non-elliptical planforms.93

On the empirical side, the war effort called for wind-channel studies of the drag generated by different aircraft components such as undercarriages and machine-gun mountings, engine-cooling systems, and the ubiquitous struts and bracing wires of the period.94 Work was also done on the lift and drag of the fuselage, the interaction between the fuselage and the wing, the effect of dividing the wing, the forces on fins and rudders, and the empirical properties of the triplane configuration.95 Experiments were done to test the resistance of the nose shapes required by different engine types, for example, rotary as compared with in-line engines, and attempts were made to add rotating propellers to the wind-channel models to achieve realism.96 Some wind-channel tests were also done on models of complete aircraft.97 Munk and Cario continued the studies initiated by Foppl of the downwash behind a wing. Whereas Foppl had worked with the overall force exerted by the down – wash on the elevator, Munk and Cario studied the downwash in much more empirical detail, using fine silk threads to trace the local variations. They un­covered significant complexities in the flow and made clear the need for a more extended program of work.98

Numerous studies were carried out to measure the lift and resistance of individual wing profiles. These were mainly overseen by Munk and his col­laborator Erich Huckel.99 Significant efforts were made to ensure that the re­sults were intelligible to those who might use them in practice.100 An attempt was also made to introduce order into the vast amount of data that had accu­mulated for different aerofoils, though the classification remained largely at the empirical level.101 One trend was toward an interest in thicker rather than thinner aerofoils, something that surprised the British when they examined captured German aircraft.102 An example of these thick aerofoils was the Got­tingen 298 used on the famous Fokker triplane. The use of the 298 profile by the designer Anthony Fokker does not, however, appear to have been a con­sequence of Prandtl’s recommendation or scientific knowledge of its good lift and drag characteristics (characteristics that, a priori and wrongly, the British designers doubted). In fact, the aerofoil was introduced into the Fokker pro­duction line by their chief engineer Reinhold Platz on the basis of trial-and – error knowledge. Later, and unknown to the people at Fokker, it was tested in Gottingen, where it was given its designation.103

The Fokker episode indicates that there was a continuing gap between the “practical men” of Germany and those self-consciously developing science- based procedures and working in academic and government institutions. The alienation of the practical men was not purely a British phenomenon, though it seems to have been less acute as a problem for German aviation than for British. Evidence in the technical reports indicates that the members of the Gottingen school were themselves aware of this gap and found it frustrating. Max Munk addressed the issue directly in a brief report of October 15, 1917, titled “Spannweite und Luftwiderstand” (Span and air resistance).104 Refer­ring to the practical conversion formulas linking wings of different aspect ratio, Munk complained:

Die kurzlich von Betz veroffentlichen Prandtlschen Flugelformeln werden wohl, da sie auf theoretischen Grundlagen beruhen, in der Praxis nicht so freundlich aufgenommen werden, wie sie verdienen. Das ist sehr schade, denn die Formeln enthalten mehr und leisten Besseres als der Praktiker geneigt ist, ihnen zuzutrauen. (199)

The formulas of Prandtl’s wing theory that Betz has recently published will probably not be welcomed in the realm of practice as much as they deserve because they rest on theoretical grounds. This is a great shame because the formulas offer more and give better service than the practical man is inclined to believe.

Munk went on to give an explanation of the significance of the formulas for the aircraft designer and some simple, general rules for the rapid calculation of the induced resistance and angle of incidence. Despite this evidence of skepticism in certain quarters, there was no shortage of contract work to be done for individual aircraft firms during the war years. This is attested by the frequency with which such names as AEG, Aviatik, Rumpler, Siemens and Schuckert, and Zeppelin were mentioned in the technical reports. Despite the problems of communication between the representatives of theory and practice, Prandtl’s institute had achieved a central position in what would now be called the military-industrial complex of Wilhelmine Germany. If this development brought frustrations as well as the advantages of government support, it is clear that striking progress had been made in aerodynamics, both empirically and theoretically.

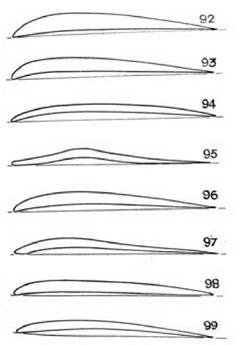
One of the more unusual aerofoils whose properties were reported on by Munk and his colleagues was designated as profile 95. Visually it stood out from the usual run of aerofoil shapes (see fig. 7.16). The aerofoil looked like the back of a cat when the animal stretched, and it was duly given the nick­name Katzenbuckelflache. The Gottingen tests showed that the performance characteristics of the “cat’s-back” profile 95 were notably poor. It was tested by Max Munk and Carl Pohlhausen in the course of a run of work on nearly one hundred aerofoils. The results were listed together in the Technische Ber – ichte of August 1917 and showed that the maximum-lift coefficient for each wing in this sequence was typically in the region of 130 or 140. The maxi­mum lift coefficient for profile 95, by contrast, was given as 95.2. Again, the maximum lift-to-drag ratio was typically 14 or 15, while the ratio for profile 95 was 10.8.105 The designer of the cat’s-back wing was the celebrated physicist Albert Einstein.106 In retrospect Einstein felt that his excursion into aerody­namics had been irresponsible—he used the word Leichtsinn. From 1915 to

figure 7.16. Profile 95 stands out because of its unusual shape. It is the “cat’s-back” wing designed by Albert Einstein. From Air Ministry 1925, publication no. 1120.

1917, Einstein had been a consultant to two aircraft firms, LVG and Merkur, and an aircraft had been equipped with the Einstein wing. The test pilot for LVG, Paul Ehrhardt, barely managed to get the machine off the ground and gave his professional opinion on the wing by saying that the airplane flew like a pregnant duck.107 The Gottingen tests made the same point in more scientific terminology.

No account remains of how Einstein actually designed the wing, but some insight into his thought processes may be gained from an article he published in 1916 in Die Naturwissenschaften. Here he set out to explain, in elemen­tary terms, the basic principles of lift.108 How does a wing support an air­craft and why can birds glide through the air? Einstein declared, “Uber diese Frage herrscht vielfach Unklarheit; ja ich mufi sogar gestehen, dafi ich ihrer einfachsten Beantwortung auch in der Fachliteratur nirgends begegnet bin” (400) (There is a lot of obscurity surrounding these questions. Indeed, I must confess that I have never encountered a simple answer to them even in the specialist literature). This is a striking claim, given that Einstein was writing a number of years after the publications of Kutta, Joukowsky, and Prandtl.

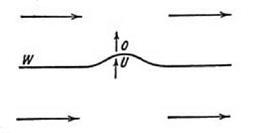
Einstein drew an analogy between the flow of fluid through a pipe of vari­able cross section and its flow around a wing. As fluid passes along a pipe that gets narrower, the fluid speeds up. By Bernoulli’s law the pressure will be lower in the fast, narrow section than in the broader section. Einstein then invited the reader to consider a body of incompressible fluid with no signifi­cant viscosity (that is, a perfect fluid) which flowed horizontally but where the flow was divided by a thin, rigid, dividing wall. The wall was aligned with the flow except that it also had a curved section where the wall bulged up­ward. (See fig. 7.17, which is taken from Einstein’s paper.) The curved section looks a bit like a cat’s back and would appear to have the same shape as the underside of the Einstein wing tested at Gottingen. Einstein argued that the fluid above the dividing wall will behave like the fluid in a pipe when it en­counters a narrowing of the pipe and will speed up and exert a diminished pressure on the wall. The fluid below the wall will behave like the fluid in a pipe when it encounters a widening out of the pipe so it will slow down and increase the pressure on the wall. The fluid pressure pushing upward on the curved section of the dividing wall will thus be in excess of the pressure push­ing downward, so there will be a resultant force upward All that is necessary now is to imagine that most of the dividing wall has been removed, leaving behind just the curved section. This procedure, argued Einstein, will retain the features of the flow that generate the pressure difference and hence will represent a wing with lift.

Einstein’s argument rested on the assumption that the removal of all but

figure 7.17. Flow through a variable cross section. Below the wall W, the fluid slows down so the pressure increases; above the wall the flow speeds up so the pressure decreases. This theoretical argument appears to be the basis of the cat’s-back wing. From Einstein 1916. (By permission of the Albert Einstein Archives, Jerusalem)

the curved portion of the dividing wall would leave the flow unchanged at the leading and trailing edge of the remaining arc. He appeared to take this as ob­vious: “Um diese Kraft zu erzeugen, braucht offenbar nur ein so grofies Stuck der Wand realisiert zu werden, als zur Erzeugung der wirksamen Ausbiegung der Flussigkeitsstromung erforderlich ist” (510) (To generate this force it is obviously only necessary for part of the wall to be real. It need only be suf­ficiently large to produce the effective curvature of the flow). It is puzzling that Einstein made no mention of circulation. Was he aware of the circulation theory of lift? This remains unclear, but given that he assumed the air to be a perfect fluid, it makes it all the more important to ask how he proposed to circumvent d’Alembert’s paradox. How did Einstein expect to get a lift force rather than a zero resultant?

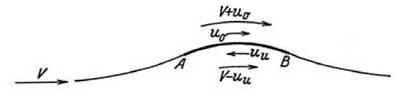
Although Einstein wrote in a dismissive way about the aerodynamic liter­ature, he had, in effect, taken the discussion back to where Kutta started it in 1902. When, following Einstein’s instructions, all of the wall dividing the flow is removed except for the curved piece, what is left is essentially Kutta’s arc at a zero angle of incidence. Einstein did not specify that the curve he discussed in his article was precisely the arc of a circle, but his argument was offered as a general one. If it were right it would apply to Kutta’s arc. But it does not. The arc is a counterexample to what seems to be Einstein’s argument, that is, to any argument that depends on ideal fluids but does not make provision for circulation. In order to generate lift, and to generate the requisite speed dif­ferential between the upper and lower surfaces of the arc, a circulation must be postulated. In a continuous perfect fluid flow, without an independently specified circulation, such an arc would not produce lift. D’Alembert’s para­dox would come into play. Such an arc would not have its stagnation points on the leading and trailing edge. The formula for the complex velocity has singular points indicating infinite velocities for the ends of the arc.109

figure 7.18. Flow of an ideal fluid with circulation around an arc. As Kutta showed in 1902, a circula­tion is necessary to place the stagnation points on the leading and trailing edges, that is, at A and B. As shown here, Prandtl’s diagram, unlike Einstein’s, makes the role of circulation explicit. From Tietjens 1931, 174. (By permission Springer Science and Business Media)

In his diagram Einstein put the stagnation points on the leading and trail­ing edges of the arc even though he did not explicitly invoke a circulation. He put them where they would have been, given the appropriate amount of circulation needed to avoid infinite velocities at the edges. He did this by sup­posing that the guiding effect of the dividing wall, smoothly leading the fluid toward, around, and then away from the arc, would still be present even when the wall was removed and only the arc was left. There are no grounds for this assumption. Perhaps the best that can be said is that Einstein had, in fact, made provision for circulation in his analysis, but had done so tacitly and by questionable means. In his published lectures, a few years later, Prandtl gave a diagram that was almost identical to Einstein’s but, in Prandtl’s case, the com­ponent of circulation in the flow was properly identified and made explicit.110 Prandtl’s diagram is reproduced as figure 7.18 for purposes of comparison with Einstein’s figure.

It would seem that Einstein had little knowledge of current developments in the field of aerodynamics. This episode is a salutary reminder of the differ­ence between fundamental physics and technical mechanics. Eminence in the former does not guarantee competence in the latter.