Prandtl and Fuhrmann on Airship Resistance

Georg Fuhrmann had been Prandtl’s pupil at the technische Hochschule in Ha­nover, where his ability in the course on technical mechanics caught Prandtl’s attention. After completing his training as an engineer in 1907, Fuhrmann joined Prandtl at Gottingen and played a significant part in setting up the wind tunnel. It was Fuhrmann in 1910 who wrote the review of the German translation of Lanchester for the Zeitschrift fur Flugtechnik.1 His warm rec­ommendation stood in marked contrast to the coldness of the Nature re­view. In 1911 Fuhrmann carried out important theoretical and experimental research on the resistance of model airships. He was to die in action in the first few weeks of the war in 1914.18

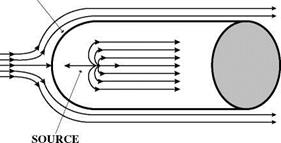
The experiments were designed to compare the predictions of ideal-fluid theory with wind-tunnel measurements.19 To make his theoretical predic­tions Fuhrmann had used a standard technique from classical hydrodynam­ics in which complex flows were built up from simpler flows, for example, from an array of sources and sinks, each of which can be represented by a simple velocity potential. He assumed a theoretical distribution of sources and sinks in a uniform flow of perfect fluid and arranged them in such a way that they gave rise to airship-like configurations of streamlines. The basis of Fuhrmann’s procedure can be conveyed intuitively by examining figures 5.2 and 5.3. If a source is combined with a uniform flow, then the fluid from the source pushes the free stream aside as shown in figure 5.2. At the same time the streamlines radiating out from the source are distorted and bent back. The streamlines of the new flow coincide with the streamlines of the flow around a long, blunt-nosed body. Selecting an appropriate streamline of the new flow and imagining that it is suddenly solidified gives the surface of the body.

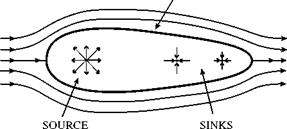
If now a line of sinks is introduced directly downstream of the source and spread along the axis of the body, the overall flow is modified once again, as in figure 5.3. The fluid injected into the flow at one point by the source is now drawn out of the flow at other points by the sinks. If the intake of the

‘SOLIDIFIED’ STREAM LINE figure 5.2. A single source in a uniform flow of ideal fluid creates a flow pattern similar to that around a blunt-nosed object of infinite length. The surface of the object consists in an appropriate streamline of the flow that is imagined to be solidified.

‘SOLIDIFIED’ STREAM LINE figure 5.3. Fuhrmann and Prandtl used a system of sources and sinks placed in a uniform flow of ideal fluid to simulate the flow around a closed solid. An appropriate distribution of sources and sinks produces streamlines similar to those over an airship.

sinks equals the output of the source, the streamlines of the combined flow can close up again. While the obstacle represented in figure 5.2 was infinitely long, the obstacle in figure 5.3 is of finite length and resembles the outline of the hull of an airship. Fuhrmann used Bernoulli’s law to calculate the pres­sures at various points on its surface. These surface pressures, in accord with d’Alembert’s paradox, summed to zero, but it was the distribution of pres­sure that was the focus of interest.

By assuming different distributions of sources and sinks, Fuhrmann could produce theoretical configurations representing different shapes of airship, for example, some with blunter noses or longer tails than others. He worked out the streamlines for six different shapes. The next step was to construct a set of hollow model airships, made out of metal, which accurately conformed to these theoretically generated shapes. Fuhrmann placed the models in the Gottingen wind tunnel and measured the pressures at a number of points on their surface. He did this by means of small holes in the surface that were con­nected to a manometer. Next, after removing the holes and piping, the mod­els were suspended from wires and attached to scales so that wind-tunnel measurements could be made to find their total drag.

Careful corrections had to be made to allow for both the resistance and the stretching of the supports. Fuhrmann conceived of the drag on the airship as divided into two parts: the pressure drag and the friction drag. The pres­sure drag was the result of pressures normal to the surface; the friction drag was tangential. Normal pressures could be generated by a perfect fluid, but it takes a viscous fluid to create a tangential traction. Fuhrmann reached three important conclusions. First, the graph of the observed pressure distribution of the air flow was very close to that predicted from ideal-fluid theory except at the very tail of the airship models. The only exception was a blunt-nosed model, where there was deviation from the predicted pressure at the nose as well as the tail. Second, models with a rounded nose, slender body, and long tapered tail had astonishingly low resistance, for example, at 10 meters per second they had less than one-twentieth of the resistance of a sphere of the same volume. Third, nearly all of this small, residual drag could be accounted for by the frictional drag of the air on the surface. Even given the slight devia­tion at the tail and, of course, the effect of the air in immediate contact with the surface of the airship, the air behaved like an ideal fluid.

In the period immediately after the Great War, Prandtl wrote an account of the Gottingen airship work for the American National Advisory Com­mittee for Aeronautics. It appeared in 1923 in English as the NACA Report No. 116.20 The first part of the report included a survey of ideal-fluid theory, and the second part began with an account of the resistance measurements on model airships carried out by Fuhrmann. Prandtl declared that the agree­ment between theory and experiment in Fuhrmann’s work had given them “the stimulus to seek further relations between theoretical hydrodynamics and practical aeronautics” (174). “Theoretical hydrodynamics,” here, meant perfect fluid theory. Even more striking was how Prandtl described the char­acter of the agreement that had so encouraged them. “The theoretical theo­rem that in the ideal fluid the resistance is zero,” he said, “receives in this a brilliant confirmation by experiment” (174).

Prandtl’s British counterparts such as Bairstow, Cowley, Lamb, Levy, and Taylor did not speak in this way. For the British, a “theoretical theorem” would be the result of deduction from the premises of the theory and would be something to be judged by logical, not experimental, criteria. It described an ideal fluid not a real fluid. Even if ideal-fluid theory could, on occasion, generate an empirically correct answer, this would only be because false premises can sometimes produce true conclusions. Properly speaking, exper­iment could never provide a “brilliant confirmation” of what was essentially a mathematical theorem, and certainly not of a theorem that referred to an acknowledged mathematical fiction. The first would be wholly unnecessary and the second wholly impossible.

Prandtl’s enthusiastic formulation was slightly qualified when Fuhrmann’s experiments were discussed in his Gottingen lectures, which were published a few years later.21 In 1931 Prandtl described Fuhrmann’s result as follows:

Diese Tatsache kann man bis zu einem gewissen Grade als einen experimen – telien Nachweis ansehen fur den Satz der klassischen Hydrodynamik, dafi in einer reibungslosen Flussigkeit der Widerstand eines bewegten (hier aller – dings stromlinienformigen!) Korpers Null ist. (153)

Up to a certain degree one can regard this fact as an experimental proof of the classical hydrodynamic theorem that the resistance of a moving body (at least, a streamlined one!) in a frictionless fluid is zero.

The brilliant confirmation had become a proof up to a “certain degree,” but when Prandtl came to spell out the basis of this more qualified judgment, it is clear that this did not bring him nearer to the British position. In his lectures, Prandtl dealt with Fuhrmann’s work in a section devoted to bod­ies of small resistance. He introduced the section by identifying the area in which inviscid theory has a legitimate application to the real world. It was, he said, an area of great technological significance and included airships, aircraft wings, and propellers.

Wahrend die klassische Hydrodynamik der reibungslosen Flussigkeit durch – weg in allen denjenigen Fallen versagt, in denen es sich um Stromungsvor – gange mit betrachtlichem Widerstand handelt, lasst sie sich mit Vorteil an – wenden bei Flussigkeitsbewegungen mit geringem Widerstand. In den meisten praktischen Fallen—so besonders in der Flugtechnik und im Luftschiffbau— handelt es sich aber darum, den meist schadlichen Widerstand auf ein Min – destmafi zu bringen, so dafi gerade hier ein grosses Anwendungsgebiet der Methoden der Hydrodynamik reibungsloser Flussigkeiten vorliegt. Auf die – sen Umstand ist es zuruckzufuhren, dass die Flugtechnik und Luftschiffahrt so ausserordentlich durch die neueren Untersuchungen der Luftbewegungen (Luft aufgefasst als reibungslose Flussigkeit) gefordert wurde—wir erinnern nur an die Ausbildung der gunstigsten Luftschifform, an die Tragflugel – und Propellertheorie—und dass umgekehrt die praktischen Probleme der Flug – technik der Theorie eine grosse Anzahl dankbarer Fragestellungen gegeben haben. (150-51)

While the classical hydrodynamics of a frictionless fluid always fails in those cases where the flow must cope with a considerable resistance, it can be ap­plied with advantage to fluid motion with small resistance. In most practical cases—particularly in aviation and the construction of airships—it is a mat­ter of bringing the most damaging forms of resistance down to a minimum. It is precisely here that there lies a large field for the application of the methods of the hydrodynamics of frictionless fluids. It is for this reason that aviation and airship travel received such benefit from the new investigations into the flow of air (where the air was conceived as a frictionless fluid)—one calls to mind the development of the most satisfactory shapes for airships, and wing and propeller theory. Conversely, the practical problems of aviation have pre­sented to the theory a large number of fruitful questions.

This passage gives Prandtl’s argument for conceiving air as a friction­less fluid. Lamb kept the two things separate, putting one in a box marked

“real” and the other in a box marked “ideal.” Prandtl put them both in the same box.

Giving theory and experiment the same referent is necessary for turning d’Alembert’s result from a mere theorem into a genuine paradox. This was why Lamb adopted the strategy of assigning them separate referents. In giving them the same referent, did Prandtl intend to generate or embrace a paradox? Or, if this was not his intention, was it the unwitting consequence of his posi­tion? The answer is neither. Prandtl’s stance was not paradoxical. He avoided paradox, but he did so by rejecting precondition (1) rather than, as Lamb did, precondition (2). To create a paradox it is necessary that two sources of infor­mation about a common object contradict one another. Prandtl said they did not contradict one another. The theory predicted zero resistance—and this was (very nearly) what was found by experiment.

The situation here was not, as G. P. Thomson might suspect, a case of en­gineers working in the realm of “good enough.” It was the opposite. Prandtl and Fuhrmann found they could use the theory of ideal fluids to design air­ships that were very close approximations to the zero resistance entailed by the theory of perfect fluids. It helped them to identify the places where smooth flow was breaking down so that they could reduce it further. Their efforts were informed by an ideal they were striving to attain. The ideal was not kept distinct from practice, or set in opposition to it, but was integral to it and gave practice its direction and purpose. Max Munk, a distinguished pupil of Prandtl, looking back over some seventy years, recalled the Prandtl and Fuhrmann experiments and clearly thought that their methodological significance had not been properly appreciated.22 Munk said: “The wind tunnel was asked whether the actual pressure distribution was sufficiently equal to the one computed for a perfect fluid. It was asked whether the study of the motion of a perfect fluid was helpful for practical aerodynamics. The wind tunnel answered with a loud Yes. This was a very great achievement of Prandtl, one for which he did not get enough credit” (1). Munk did not indicate who had been reluctant to give due credit, but it is clear that, had he wished to do so, he could have pointed to the British stance and the method­ological assumptions behind it.