The Mathematical Definition of Circulation

The behavior of a simple vortex, of the kind just described, can be used to introduce the mathematical definition of the quantity called “the circulation” of a flow.7 So far I have used the concept of circulation in an intuitive way, but for the purposes of aerodynamics it was important to deploy a precise definition. To follow the history of the dispute over the circulatory theory of lift, readers must grasp the general features of the more precise, mathemati­cal concept. I introduce them in two stages. First I confine the discussion to a simple, isolated vortex of the kind already introduced and then I move to a more general definition that can be used to detect and measure circulation in complicated flows where the vortex is just one component. The ideas dis­cussed in this section are now standard, textbook material, but that was not always the case. They found no place in Cowley and Levy’s textbook of 1918. These authors were still under the influence of the discontinuity theory of lift and did not take the circulation theory seriously.

Consider again the family of simple vortices where the streamlines are concentric circles of radius r and the uniform speed of flow along the stream­lines (the tangential velocity v) diminishes in proportion to the distance r of the streamline from the center of the vortex. This model has already been expressed by the formula v = k/r, where k is the constant of proportional­ity. Three features of this family of vortices are immediately evident. First, the product of v and r, that is, the speed along a streamline multiplied by the radius of the streamline, always has the same value, namely, k. Second, as the radius r gets very small, the velocity v gets very large. Mathematically, as r ^ 0, v ^ ro. Third, as r gets very large, the velocity of the flow gets very small. In the limit, as r ^ ^, then v ^ 0. The flow is effectively stationary at great distances from the center of the vortex. All vortices of this simple kind therefore cover the entire range of velocities from infinite velocity at the cen­ter to zero velocity at the distant periphery. The situation at the very center of the vortex, at r = 0, where the flow rotates at infinite speed, is obviously physi­cally unrealizable. It indicates the abstract character of the vortex model. The problematic point at r = 0 is called a “singular point” of the formula.

Intuitively some vortices are said to go faster than others or to be stron­ger than others. How are these distinctions to be expressed given that the simple k/r formula covers the full range of velocities from zero to infinity? The answer is that at any given distance from the center, the speed of flow of some vortices will be greater than others at that distance. In order to make the distinctions that are desired, the speed of flow must always be related to the distance from the center. This requirement must be built into any definition of the strength of a vortex. Such a relation is embodied in the constant k that has already been introduced in the formula relating tangential speed v and radius r. The constant k characterizes a vortex and distinguishes the faster from the slower vortices. For any given distance r from the center, the bigger the value of k the faster the vortex goes.

Suppose now that the word “circulation” is introduced with the aim of describing a vortex. The aim is to discriminate between them so that a fast, strong vortex has a “greater circulation” than a slower, weaker vortex. One plausible candidate for the definition of the concept would be to equate cir­culation with the value of k. Historically the chosen definition was close to this but not identical. The measure of circulation that was chosen made it proportional to k but not equal to k. It was decided that the circulation was to be 2nk. Stated in words, the circulation around a simple vortex was defined as the product of the tangential velocity v along some streamline and the circumference of the streamline, which is 2ПГ. This (provisional) definition refers to the speed along a contour multiplied by the length of the contour. Using the symbol Г (gamma) for the circulation, the circulation around a simple vortex is given by the formula Г = v 2ПГ or by the formula Г = 2nk. The value of the circulation around a given vortex has the property that it comes out the same whatever streamline is used to arrive at the value.

The next step is to generalize the definition so that it is not tied to flows with circular streamlines. The move toward generality exploited the fact, noted earlier, that in a simple vortex it does not matter which circular stream­line is used to arrive at the value of the circulation. The circulation could be computed in part by using the speed vj along an arc of the circle of radius r1 and in part by using the speed v2 along an arc of the streamline of radius r2 (see fig. 4.4a). The jump from one arc to the other could be taken along an appropriate radius. The jump would not contribute to, or alter, the circula­tion because all the speed in the vortex is tangential and the speed along any radius is zero. As long as the two circular arcs were combined so as to make a closed circuit around the vortex, the value of the circulation would be no different from the value calculated using a single circular streamline as the relevant contour. And what holds for jumping between two different circular streamlines holds for jumping between three or four or any number. This too makes no difference to the value attributed to the circulation. In the limit, the jumps can be imagined to be so numerous, and the streamlines can be imag­ined to be so close, that the contour along which the circulation is computed could weave any path through the field of flow (see fig. 4.4b). The upshot is that the contour can be arbitrary. All that matters is that it forms a closed loop around the center of the vortex.

In the original definition of circulation around a simple vortex, where the contours were concentric circles, the speed used in the calculation was the tangential speed along the circumference. When the contour is arbitrary, the speed used in the computation must be the speed along this arbitrary contour. Stated generally, at any point P on the contour, the flow can be as­sumed to have a speed q and a direction that makes an angle 0 to the contour (see fig. 4.5). To compute the circulation, the component of speed along the contour, namely, q cos0, must be used. The contribution to the circulation at that point is dГ = q cos0 ds. Summing or integrating this quantity around the closed contour gives the circulation around the contour. This leads to the general definition of the circulation Г around a closed contour C as

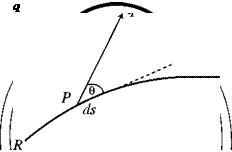figure 4.4. In (a) the product of the speed and circumference is the same for all streamlines of the vortex. The value of the circulation can therefore be computed using a contour that jumps from one streamline to another. Part (b) shows how this fact can be exploited and any contour used to compute the circulation. An arbitrary contour can be thought of as a limiting case involving an infinite number of jumps. The strength of the circulation is thus contour-independent provided that the contour encloses the vortex.

figure 4.5. The speed of the flow at P is q. The component of q along the curve RS is q cos0. The “flow” along RS is defined as Jqcos0ds where the integration is taken along the contour RS. If the contour is extended to form a closed loop, the flow counts as the “circulation” around the closed contour.

Г= I qcosOds

The previous, and provisional, definition of the circulation around a sim­ple vortex can now be seen as a special case of this more general definition. In the special case, C is a circle of radius r. The speed q is equal to the constant tangential velocity v and always lies along the contour so that cos0 = cos 0 = 1.

These constant quantities can be taken outside the integral sign, leaving a line integral which equals the circumference 2ПГ. Thus, as before, the circulation around the vortex is Г = v2TCr.

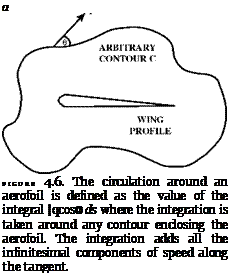
The general definition identifies a circulation in a flow even when the vor­tex merely acts as one component. If there are no vortices in the flow, the cir­culation is zero. The important point for aerodynamics, and the circulation theory of lift, is that the measure of circulation should be independent of the contour so the selection of the contour can be arbitrary, as in figure 4.6. All contours that form a closed loop containing an aerofoil, and the vortex that it is assumed to generate, should yield the same measure for the circulation around it. A large circle could be drawn around a two-dimensional aerofoil, or a rectangle could be used, and the numerical value of the integral along these contours should be the same.

Where the integral produces different values for different contours, the concept of “the circulation of the flow” is not well defined. This can happen, for example, when the fluid is viscous. Contour-independence will prove to be of great significance later in the story, when I describe how, in the 1920s, the personnel of the National Physical Laboratory attempted to conduct ex­periments to establish, once and for all, whether the circulation theory gave the right account of the lift of a wing moving through air.8