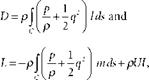Category The Enigma of. the Aerofoil

There was clearly a desire by the members of the Aeronautical Research Committee to put the theory of circulation and Prandtl’s analysis of the finite wing to the test, but disagreement emerged about how to proceed. This gave rise to a sequence of technical reports in which Taylor and Glauert crossed swords. Part of the problem concerned experimental technique. A further difficulty was that Glauert was sensitive to the fundamental distinction be­tween the ideas underlying the two-dimensional picture of Kutta flow (that is, flow that is smooth at the trailing edge) and Prandtl’s three-dimensional picture of the wing as a lifting line with trailing vortices. Glauert wanted these ideas kept distinct, while other participants in the discussion ran these two ideas together and counted them as forming one single theory whose basic assumption was the irrotational character of the flow.

To explain what was at issue it is necessary to go back to December 1921 and the mathematical report submitted by Muriel Barker.4 She had suggested that the theoretical streamlines she had plotted for the flow over a Joukowsky aerofoil with circulation could be the basis for an experimental test: “it would be most instructive,” she had written, “if these same quantities could be ob­tained practically” (3). Miss Barker’s report and the question of what to do next were discussed by the Aerodynamics Sub-Committee and by the full Research Committee during February and March 1922.5 Should they follow her suggestion and place a model of a Joukowsky aerofoil in a wind channel or should they use a more practical aerofoil, for example, the RAF 15? If they used a real section then should they ask Miss Barker to generate the theoreti­cal streamlines by tedious computation or could a quicker method be found? Were mechanical or electrical methods of generating the theoretical stream­lines of comparable accuracy to those produced by the laborious calculations that would be needed? Lamb was in favor of using the Joukowsky profile and direct calculation. Southwell wanted to use a more realistic profile and a me­chanical method. He mentioned that Taylor had developed a piece of appara­tus that enabled him to use a soap film to model the potential surfaces of ideal fluid flow. Bairstow added that he and Sutton Pippard had devised graphical methods for solving Laplace’s equation.6 Then there was the possibility of using the techniques developed by Hele-Shaw derived from photographs of creeping flow. It was decided that Southwell and Taylor would report back on different analogue methods of producing theoretical streamlines.

Southwell started with his report T. 1696.7 He supported Muriel Barker’s suggestion that comparisons be made of theoretical and empirical stream­lines for an infinite wing, that is, where the model wing would reach right across the tunnel to exclude the effect of flow around the tips. In this way, said Southwell, “a direct check can be imposed upon one of the fundamental assumptions of the Prandtl theory” (2). Southwell then described the method developed by Taylor for simulating the streamlines and the bench-top ap­paratus that had been built.8 A soap film was stretched between the walls of a box while precise measurements were made of the position of the film. The film connected the outline of a small wing profile to other boundaries within the confines of the box. (These boundaries represented the walls of the wind tunnel.) Southwell explained how this technique could take into account the circulation as well as automatically correcting for the effect in the flow of the tunnel walls. “Using orthodox mathematical methods,” said Southwell, “it would appear that the problem thus presented is one of extreme difficulty”

(2) . Taylor, however, followed this up with a brief note, designated T. 1696a, in which he said that he had actually applied the soap-film method to a model aerofoil but had not taken the matter further.9 The small size of the apparatus prevented the measurements being made with the required accuracy. Tay­lor therefore backed the use of an electrical method, and eventually such a method was developed by E. F. Relf and formed the basis of the experimental comparisons that were later published.10

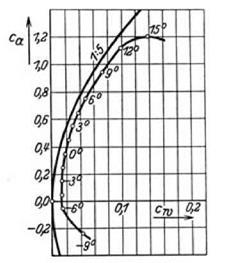
At this point Glauert intervened. In May 1922 he submitted his “Notes on the Flow Pattern round an Aerofoil” (T. 1696b).11 First, he took issue with Southwell’s claim that it would be difficult to allow for the influence of the channel walls by use of analytical methods. Glauert said that the effects could be represented in a simple way using standard mathematical techniques, the so-called method of images. He then went on to make some comments about the proposed experimental comparison involving an infinite wing and two­dimensional flow. It was important “to have a clear understanding of its bear­ing on the general question of aerofoil theory” (2). The implication was that some of the thinking behind the proposal lacked the requisite clarity. Not every test of the two-dimensional work was automatically a test of the three­dimensional claims, for example, the hypothesis that the flow over a wing is smooth at the trailing edge is not a necessary presupposition of Prandtl’s work. Prandtl used the idea that lift is proportional to circulation and that the circulation around a wing can be replaced by the circulation around a line vortex, that is, that the chord is negligible. But, said Glauert, no assump­tion is made “as to the relationship between the form and attitude of the aerofoil and the circulation round it, the analysis always being used only to estimate the behaviour of one aerofoil system from the known behaviour of another system of the same aerofoil section” (2). Taken in its own terms, he went on, the Prandtl theory has been applied “with considerable success” to three cases: (1) the effect of changes of aspect ratio, (2) the estimation of the behavior of multiplane structures on the basis of monoplane data, and (3) the description of flow patterns such as downwash. The comparison of predicted and observed data shows that the “agreement is reasonable.” This, Glauert insisted, constitutes “a satisfactory check of the fundamental equation” (3).

Glauert acknowledged that the hypothesis that the rear stagnation point is on the trailing edge overestimates the circulation and therefore the lift. It does so because of departures from the idealized condition of irrotational flow. The real flow detaches itself from the top surface of a wing before reach­ing the trailing edge and forms a “narrow, eddying wake behind the aerofoil.” Glauert had discussed this in his earlier report, “Aerofoil Theory,” but the committee seemed to be using the well-known facts about the existence of a turbulent wake as an objection to Prandtl’s work. If the wake really was to be a focus of interest, it would be necessary to make assumptions about the distribution of vorticity associated with “the contour of the aerofoil and in­side the wake region.” Prandtl’s aim was to give a first-order approximation for the flow at a distance from the aerofoil, and at points outside the wake. The vorticity of the aerofoil can then be concentrated at a point or, in the three-dimensional case, in a line, just as Prandtl assumed. It is legitimate un­der these circumstances to “ignore completely the series of alternative small vortices in the wake” (4). Glauert concluded by saying that the proposed ex­periment on an infinite wing would, indeed, illuminate the relation between aerofoil sections and the circulation round them, “but will not have any bear­ing on Prandtl’s aerofoil theory” (4).

Taylor did not agree. He produced a written reply, designated T. 1696c, in which he challenged both Glauert’s response to Southwell about mathemati­cal techniques and Glauert’s claim that the experiment would be irrelevant to Prandtl’s theory.12 On the latter point, Taylor declared that all the reasons Glauert “brings up to support his view were well known to most of the Com­mittee which discussed the proposed experiments and some of them were actually brought up in the discussion. It is curious, therefore, that Mr. Glau – ert should come to a view which is different from that of the members who proposed the experiments” (1).

Taylor said that the experiment on the infinite wing would constitute a test of Prandtl’s theory because the theory was based on the assumption

that the flow at a distance from the wing was irrotational. Glauert’s posi­tion, it seemed to Taylor, was that this assumption can be made a priori, but it cannot. It is an empirical matter, and the proposed experiment was designed to test it. Second, Glauert had said that the experimental evidence gathered so far had provided a satisfactory check on the fundamental equa­tions of the theory. Taylor replied that if “satisfactory” meant “sufficient” he could not agree. The fundamental equation L = p V Г, relating lift and circu­lation, might hold true for some body of data, and some experimental ar­rangement, but not for the reason that Prandtl had given, that is, not because the flow was irrotational. In fact, said Taylor, “there are an infinite num­ber of kinematically possible distributions of velocity for which this is the case, but only certain of them will correspond with irrotational motions”

(3) . Finally, Taylor turned to Prandtl’s assumption that the chord of the wing could be neglected. Again, insisted Taylor, this could not be assumed a pri­ori. “The assumption can only be justified by experiment or by calculation of the type indicated by Miss Barker or by the purely empirical method of comparing the results of Prandtl’s calculations with observed lifts and drags”

(4) . For these reasons, said Taylor, “I do not agree with the conclusions reached by Mr. Glauert.”

One of the subcultures I identify in my explanation (German technical me­chanics) belongs to the general field of technology, while the other (British mathematical physics) falls more comfortably under the rubric of science. My explanation therefore presupposes a society in which technological and sci­entific activity are understood to be different from one another. The picture is of culture with a division of labor in which the roles of technologist and scientist are treated as distinct or distinguishable. These labels are the catego­ries employed by the historical actors themselves. Their role in my analysis derives from their prior status as actors’ categories.15 Although the members of the two subcultures interact with one another, my data justify attributing a significant degree of independence to them. To speak of “subcultures” car­ries the implication that the practitioners within each respective subculture routinely draw upon the resources of their own traditions as they perform their work and confront new problems.16 A symmetrical stance requires that both science and technology be placed on a par with one another for the pur­poses of analysis. This injunction is directed at the analyst and is consistent with the historical actors themselves according a very different status to the two activities: for example, some of the actors may see science as having a higher status than technology. The point of the methodological injunction to be “symmetrical” is that it requires the analyst to ask why status is distributed in this particular way by the members of a group and to keep in mind that it could be distributed differently.17

Attributions of status can be expressed in subtle ways. They may take the form of assumptions (made by both actors and analysts) about the depen­dence of one body of knowledge on another. Is technology to be seen as the (mere) working out of the implications of science? Is the driving force of tech­nological innovation typically, or always, some prior scientific innovation?18 An inferior status may be indicated by an alleged epistemological dependence and a reluctance to impute agency and spontaneity to technology. The sym­metry postulate does not assert the truth or falsity of any specific thesis about dependency or independence, but it does require that such a thesis is not in­troduced into the analysis as an a priori assumption. At most the dependency of technology on science is merely one possible state of affairs among many other possibilities; for example, science may depend on technology rather than technology on science, or the two may be completely fused together or completely separate. The actual relation is to be established empirically for each episode under study. In the case of the theory of lift it is clear that the technologically important ideas worked out by Lanchester, Kutta, and Prandtl were not the result of new scientific developments. On the contrary, they exploited an old science and old results, namely, ideal fluid theory, the Euler equations of inviscid flow, and the Biot-Savart law. The shock engen­dered after the Great War by the belated British recognition of the success of this approach was not the shock of the new but the shock of the old.19 The science that was exploited was not only old; it was also discredited science— discredited, that is, in the eyes of Cambridge mathematical physicists pushing at the research front of viscous and turbulent flow.

The advocates of the circulatory theory of lift brought together the ap­parently useless results of classical hydrodynamics and the concrete prob­lems posed by the new technology of mechanical flight. The theory of lift in conjunction with the theory of stability constituted the new science of aero­nautics. Given the way that scientific knowledge was harnessed to techno­logical concerns, the new discipline might be called a technoscience. Some commentators have argued that “technoscience,” the fusing of science and technology, is a recent, indeed a “postmodern,” phenomenon, exemplified by the allegedly novel patterns of development shown in information tech­nology and computer science. Others have argued that, because the division of labor between science and technology is a relatively recent development, so their fusion into “technoscience” is, in fact, a return to the original con­dition of science.20 Did not science, in its early modern form, derive from a fusion of the work of the scholar and the craftsman?21 Whether or not this account of the origins of science is true, identifying early twentieth-century aerodynamics as an instance of technoscience would support the thesis that technoscience is not a novelty.

In the 1930s Hyman Levy, who had earlier coauthored Aeronautics in The­ory and Experiment, wrote a number of books of popular science. Along with Bernal, Blackett, J. B. S. Haldane, Hogben, and Zuckerman, Levy belonged to a remarkable group of scientists who played a significant role in British cultural and political life during the interwar years.22 One of Levy’s books was titled Modern Science: A Study of Physical Science in the World Today.23 Aero­dynamics was one of his main examples. He did not call it a technoscience, but he did offer it as an exemplary case of the unity of theory and practice. Writing from a Marxist standpoint, he cited the work of Prandtl and von Karman and offered the strange transitions from laminar to turbulent flow as evidence that nature embodied the laws of dialectics. While it is plausible to see the later developments of aerodynamics as moving toward a unification of theory and practice, the fact remains that in the early years there was a dis – cernable difference between the stance of the mathematical physicists and the engineers. The history of Levy’s contributions, and his own earlier, negative stance toward the circulation theory, underlines this point. When Levy was active in the field and working at the National Physical Laboratory, there was still a significant difference in approach between mathematical physicists and technologists—at least, between British mathematical physicists and German technologists.24 It is clear that behind the emerging “synthesis” of theory and practice, there still lay the “thesis” of mathematical physics and the “antith­esis” of engineering. Historical contingency rather than historical necessity determined the balance between them. I now look at one such contingency.

In the meantime every aeroplane is to be regarded as a collection of unsolved math­ematical problems; and it would have been quite easy for these problems to have been solved years ago, before the first aeroplane flew.

g. h. bryan, “Researches in Aeronautical Mathematics” (1916)1

The successful aeroplane, like many other pieces of mechanism, is a huge mass of compromise.

Howard t. wright, “Aeroplanes from an Engineers Point of View” (1912)2

The Advisory Committee for Aeronautics (the ACA) was founded in 1909. This Whitehall committee provided the scientific expertise that guided Brit­ish research in aeronautics in the crucial years up to, and during, the Great War of 1914-18. From the outset the ACA was, and was intended to be, the brains in the body of British aeronautics.3 It offered to the emerging field of aviation the expertise of some of the country’s leading scientists and engi­neers. In 1919 it was renamed the Aeronautical Research Committee, and in this form the committee, and its successors, continued to perform its guid­ing role for many years. After 1909 the institutional structure of aeronauti­cal research in Britain soon came to command respect abroad. When the United States government began to organize its own national research effort in aviation in 1915, it used the Advisory Committee as its model.4 The result­ing American National Advisory Committee for Aeronautics, the NACA, was later turned into NASA, the National Aeronautics and Space Administration. The British structure, however, was abolished by the Thatcher administration in 1980, some seventy years after its inception.5

If the Advisory Committee for Aeronautics was meant to offer the best, there were some in Britain, especially in the early years, who argued that, in fact, it gave the worst. For these critics the ACA held back the field of Brit­ish aeronautics and encouraged the wrong tendencies. The reason for these strongly divergent opinions was that aviation in general, and aeronautical sci­ence in particular, fell across some of the many cultural fault-lines running through British society. These fault lines were capable of unleashing powerful

and destructive forces. From the moment of its inception the Advisory Com­mittee was subject to the fraught relations, and conflicting interests, that divided those in government from those in industry; the representatives of the state from those seeking profit in the market place; the university-based academic scientist from the entrepreneur-engineer; the “mathematician” and “theorist” from the “practical man.” Throughout its entire life these struc­tural tensions dominated the context in which the ACA had to work.6

Suppose the mathematician has managed, by good fortune or guesswork, to write down the stream function for a steady flow of fluid under certain boundary conditions. By equating the stream function to a sequence of con­stants, a family of streamlines can be drawn and a picture of the flow can be exhibited. Now suppose that, guided by the streamlines, the mathematician draws another family of curves. These new curves are to be drawn so that they always cut across the streamlines at right angles. A network of orthogonal lines is built up. If the first set of lines were the streamlines of the flow, what are these new lines that have been drawn so that they are always at right angles to them?

They are called potential lines. They are in fact another way of implic­itly representing the velocity distribution of a flow. Their immediate interest is that the potential lines of a given flow can always be reinterpreted as the streamlines of a new flow, while the old streamlines become the potential lines of the new flow. Streamlines and potential lines can be interchanged, provided that appropriate changes are made to the boundary conditions of the flow. This possibility of interchange can be interpreted to mean that, just as there exists a stream function, so there must exist another, closely related function ready to perform the same role with regard to the lines of potential that у played with regard to streamlines. This function is called the potential function, and it is conventionally designated by the Greek letter phi, ф. The role of the potential function may be illustrated by the uniform flow along the x-axis, where the axis can be taken as a solid boundary. This flow is the one discussed earlier whose stream function is у = – Uy. The streamlines are
horizontal lines parallel with the x-axis, so the potential lines are vertical lines parallel with the y-axis. Now switch the potential lines and the streamlines, that is, switch the two families of curves given by у = constant and ф = con­stant. The streamlines are now vertical and parallel with the y-axis, which can be treated as a boundary to the new flow. The horizontal lines parallel with the x-axis are the new potential lines.

The intimate relationship between potential lines and the streamlines finds expression in the mathematics of irrotational flow. Because the two families of curves are orthogonal, it is possible to write the equations for the velocity components u and v of a given flow either in terms of the stream function that applies to the flow or in terms of the potential function that applies to it. The result gives rise to the following relationships between ф and у:

= dy = дф dx dy

It follows immediately from these equations that the potential function ф obeys Laplace’s equation, just as the stream function does when represent­ing an irrotational flow. One useful mathematical property of solutions to Laplace’s equation is that they are additive. If yj is a solution and y2 is a solution, then y3 = yj + У2 is also a solution. Stream functions can be added. Again, the point can be illustrated by reference to the simplest possible cases. The flow of speed U along the x-axis (yj = – Uy) can be combined with, say, a flow of the same speed U but along the y-axis (that is, the flow arrived at by switching the streamlines and the potential lines of the original flow so that y2 = Ux), and the result is another flow that moves diagonally and whose stream function is y3 = yj + У2. In this way complicated flows can be con­structed out of simple flows.

Another of the practical men—and among the most interesting—was the designer A. R. Low, of Vickers, whose name has already been mentioned. In 1912 he had lectured at University College, London, on aerodynamics and, on March 4, 1914, with O’Gorman in the chair, gave a talk to the Aeronautical Society titled “The Rational Design of Aeroplanes.”82 Low discussed the same range of ideas that I have already identified in the writings of other practical men, but he did so with a lively, critical intelligence and a breadth of knowl­edge that makes his work stand out. Since he will play a significant role in the postwar story of the reception of Prandtl’s work, Low’s position in 1914 is worth appreciating.

Low argued that hydrodynamics is useful for providing a sound, gen­eral “outlook” on fluid flow but that in order to get “reasonably accurate numerical values we shall see. . . that we are thrown back on experimen­tal methods” (137). He showed his audience the diagrams from Greenhill’s report representing discontinuous flow around plates, some of which were normal to the flow and some at an angle to the flow. These were compared with photographs of real flows taken by the Russian expert in fluid dynamics, Dimitri Riabouchinsky. There was a “strong resemblance between the theo­retical boundary line between the stream and the back water, and the experi­mental boundary line between approximately steady flow and the region of marked turbulence” (138). But although Lord Rayleigh was “the first to give a formal value” for the reaction of a fluid on a barrier, his predicted value was only about half of the observed value for the small angles relevant to aerodynamics. An error of 50 percent is “quite intolerable to physicists and engineers” (137).

Low was clear that the idea of sweep was not the way forward. He did not use the word “sweep” but spoke of an “equivalent layer.” This approach, he said, introduced a number of variables, and there was no way of apportioning the energy losses between them. There were, said Low, an infinite number of possible ways of assigning the energy losses. Perhaps experimental methods, such as injecting colored dyes into the flow, could shed light on the question, but until then the picture was essentially arbitrary (140). Only the empiri­cal study of lift and resistance was left. Low then turned to a discussion of some experimental graphs and empirical formulas produced by Eiffel. It was known experimentally that, over a wide range, resistance varied as the square of the speed. The desired equations would then have the general form R = KAV2, where R is the force on the wing, Vis the velocity relative to the air, A is the area of the wing, and K is a constant that must be empirically determined. Given the number of variables involved, such as incidence, aspect ratio, and camber, Low observed that finding a formula that yielded the correct value would not be easy. A further complication was that the performance of the wing interacts with the flow round the rest of the machine. The point that Low wanted to stress was the “formidable series of special developments of engineering science” that were necessary before designers could be confident that any given set of drawings would turn into an airplane with predictable performance and air-worthy qualities. He concluded: “That nation will take the lead whose scientists and technical engineers, and whose works engineers, and whose pilots best understand each other and work together most cor­dially” (147). This plea for cooperation and coordination was timely and well meant, but Low must have known that none of these preconditions for taking the lead was satisfied. The divisive bigotry of C. G. Grey and his ilk put an end to any of the requisite cordiality.

The conclusion must be drawn that in 1914, on the eve of the Great War, none of the British workers in the field of aerodynamics, whether they were mathematicians or practical men, had any workable account of how an airplane could get off the ground. As the lamps of Europe were going out, vital parts of the new science of aeronautics were also shrouded in darkness.83 The mathematicians had a sophisticated theory that addressed the right ques­tions but, being based on the theory of discontinuous flow, gave disconcert­ingly wrong answers. The high-status and mathematically brilliant experts of the Advisory Committee were reduced to empiricism. The practical men were simply paddling in the shallows and, with the exception of a few, such as A. R. Low, appeared to be oblivious of the fact. Their ideas were vague, confused, and frequently failed to engage with either practical experience or experimental results. The mathematicians (unlike the practical men) could handle many of the problems about stability with confidence and rigor, but on the question of the origin and nature of lift, and the relation of lift to drag, they too had been effectively brought to a standstill.

The demands of the war years that followed seemed to discourage rather than encourage any fundamental reappraisal of the British approach. As far as the fundamental theory of lift and drag were concerned, British experts came out of the war little better than they went into it. In 1919 George Pagett Thomson summed up the situation as it had appeared to the British dur­ing those years. The terms of his assessment are sobering: “In spite of the enormous amount of work which has been done in aerodynamics and the allied science of hydrodynamics there is no satisfactory mathematical the­ory by which the forces on even the simplest bodies can be calculated with accuracy.”84 Thomson’s judgment was that for British experts, practice still ran ahead of theory, as it had at the beginning of the war and as it had from the earliest days of aviation. Throughout the war British aircraft could cer­tainly get off the ground. They flew and their wings worked. For this, both the trial-and-error methods of the practical men and the experimental work done by the Advisory Committee must be thanked. But why aircraft flew remained a mystery to those of a practical and a theoretical inclination alike. Only the most general principles of mechanics could be invoked by way of explanation, but these only indicated what, in terms of action and reaction, the wing must be doing, not how and why it did it. Probing the more specific workings of the aircraft wing remained in the realm of experiment, a process consisting of case-by-case empirical testing that was guided, or misguided, by intuition.85

The examination for part II, schedule B, of the Mathematical Tripos of 1910 was held at the Senate House and began at nine o’clock on Thursday, June 2. Question 8 of part C of the paper consisted of a typical, but daunting, combi­nation of book work and problem solving.7 The question read as follows:

C8. Prove that in irrotationally moving liquid in a doubly connected region the circulation is the same for all reconcilable circuits and constant for all time.

A long elliptic cylinder is moving parallel to the major axis of its cross sec­tion with uniform velocity U through frictionless liquid of density p which is circulating irrotationally around the cylinder. Prove that a constraining force Kp U per unit length of the cylinder must be applied at right angles to the di­rection of motion, where K is the circulation round the cylinder.

To a modern reader, versed in aerodynamics, the expression Kp U would be identified as the fundamental law relating the circulation, density, and ve­locity to the lift on a wing. In modern aerodynamics it is called the Kutta – Joukowsky relation. If interpreted aerodynamically, the “elliptic cylinder” would be a mathematically simplified substitute for the cross section of a wing, and the “constraining force” would be the weight supported by the lift. It is doubtful, however, whether any of the Tripos candidates of 1910 would have thought in this way. The year 1910 was when Kutta and Joukowsky, inde­pendently, published their results in German journals, and it is unlikely that the news had reached Cambridge. Admittedly “aeroplanes,” that is, aircraft wings, had been the subject of Tripos questions in the past, but the reference had been to Rayleigh’s paper on an inclined plate in a discontinuous flow, not to his tennis ball paper.8 Thus question C8 was unlikely to have evoked aero­nautical associations. If candidates attributed any technological significance to the formula KpU, it would have referred to ballistics not aeronautics. Perhaps some of the candidates had read Rayleigh’s tennis ball paper and

Greenhill’s extension of the analysis. More probably, they were calling up in their memories the relevant pages of Lamb’s Hydrodynamics and relying on the hours of coaching and drill to ensure that their recall was accurate. A well – prepared candidate would have remembered Lamb’s treatment of the irrota – tional flow of a perfect fluid around a circular cylinder. In article 69 of both the 1895 and 1906 editions, Lamb laid out his version of the analysis originally developed in the papers of Rayleigh and Greenhill. Like these writers, Lamb was mainly concerned with trajectories, but his analysis would have given the candidates both the general idea behind the question and the derivation of a formula which included an expression identical to that of the constraining force mentioned in question C8.

After explaining how the circulation augments the speed of flow on one side of the cylinder and diminishes, or even reverses, it on the other, Lamb had gone on to calculate the forces. Rayleigh had approached the problem using the stream function, while Lamb used the velocity potential. To begin, Lamb wrote down the velocity potential ф for the flow, assuming the cylin­der moving at any angle. He then differentiated this expression with respect to time to give дф/dt. Next he derived a term for q, the velocity of the flow. These results were substituted in a general form of Bernoulli’s equation to get a value for the pressure, and the pressure was then integrated round the sur­face of the cylinder to yield the resultant force. Lamb’s treatment was more general than Rayleigh’s, although there was no mention, even informally, of the role of friction. The two components of the force on the circular cylinder came out as follows, first in the direction of motion: and then at right angles to the motion:

KpU – M ‘Udx dt

where К is the circulation, p is the density of the fluid, U is the relative veloc­ity of the fluid and cylinder, M’ = npa2 represents a mass of fluid equivalent in volume to the cylinder with radius a, while % is the angle that the direc­tion of motion of the cylinder makes with the x-axis. The term KpU can be seen on the left-hand side of the second formula. Where the conditions of steady motion were specified as they were in question C8, the derivatives dU/dt and dx/dt, giving the rate of change with time, will be zero. The only remaining force on the cylinder will then be KpU at right angles to the motion.

Recollection of this result would have helped the candidates, but it would not have given them all they needed. The examiners of the 1910 paper had added a further complication to ensure that the mere reproduction of text­book material would not suffice. Lamb’s derivation referred to a circular cyl­inder, but the examiners had specified an elliptical cylinder. This made the question more difficult and required the candidates to demonstrate a facility with elliptic coordinates and elliptic transformations. If they could make the necessary transformation, they would then be in a position, for the rest of the deduction, to follow the pattern of the simpler case given by Lamb for the circular cylinder. Candidates would then have found that all the extra complexity actually produced terms that cancelled out, or went to zero in the course of the integration, thus leaving them, in the case of steady motion, with the same resultant force of Kp U.

Senate House records for 1910 show that A. S. Ramsey of Magdalene and A. E. H. Love of St. John’s were the two examiners who would have had re­sponsibility for the hydrodynamics questions. The other examiners, A. Berry of King’s and G. H. Hardy of Trinity, would have dealt with the more “pure” topics.9 Three years later Ramsey wrote a textbook on hydrodynamics in which circulating flow around an elliptical cylinder featured prominently.10 After discussing the case of the circular cylinder, and working through some of the intermediate steps in reasoning that Lamb had omitted, Ramsey showed the reader exactly how to address the problem of the ellipse. The move to el­liptical coordinates was explained along with advice about the types of func­tion that would satisfy Laplace’s equation and hence describe a possible flow. Ramsey also included question C8 from the 1910 Tripos paper in the exercises at the end of his chapter, which was called “Special Problems of Irrotational Motion in Two Dimensions” (119).

The title of Ramsey’s chapter conveys the point that I want to make. It shows the assimilation of Rayleigh’s tennis ball paper to the theory of perfect fluid flow in two dimensions. Ramsey did not wholly bypass the role of fric­tion. At the end of his discussion of the circular cylinder case he said: “The transverse force depending on circulation constitutes the mathematical ex­planation of the swerve of a ball in golf, tennis, cricket or baseball, the circula­tion of the air being due through friction to the spin of the ball” (101). Fric­tion was therefore mentioned, but the student was told that the mathematical explanation was to be found in inviscid theory. Ramsey, like Rayleigh, knew that this “mathematical explanation” could not furnish an account of how a spinning ball created the circulation. The point was implicit in the Tripos question which had two parts. The first part asked the candidates to prove that, under the conditions of the question, the circulation is constant for all time, that is, Kelvin’s theorem. The question then called on the candidates to generalize Rayleigh’s tennis ball result within this taken-for-granted inviscid framework.

It is now easy to see how G. I. Taylor could decide that Lanchester’s work was unacceptable. Taylor would have found himself confronted with some­thing very familiar and having little relevance for his research on eddies and turbulence. He would have known all about theories of circulation based on irrotational, perfect fluids and would have known how little they had to say about physical reality. He would certainly have been familiar with the math­ematical expression Kp U. It was the sort of thing that Tripos students were expected to deduce as an exercise in mathematical manipulation. Everyone in Cambridge knew that the cyclic approach gave an expression for a force but took away the possibility of generating that force. No wonder Taylor dis­missed the theory of circulation as readily as he dismissed the theory of dis­continuity. Lanchester’s theory was not a new discovery; it was the stuff of old examination questions.

Kutta did not see leading-edge suction as calling for a purely mathematical investigation into a singular point in the equations of flow. He took it as an indicator of a practical problem. It pointed to the presence of high speeds that were physically real and which would result in the breakdown of the flow at the leading edge and the onset of turbulence. It pointed to the presence of vortices and other physical complexities. He therefore looked for an en­gineering solution by rounding off the leading edge, that is, by the provision of a thickening of the wing at the front which could then be shaped so as to prevent the breakdown of the flow. Here Kutta’s mathematics began to make direct contact with the practicalities of building an aircraft wing.

First, he made a rough numerical estimate of the lift of Lilienthal’s wing by inserting its specifications into his equations. The wing was an arc subtend­ing an angle of 2a = 37°50/ and having a curvature giving a maximum height of 1/12 of the chord length. The angle of attack в was set at в = a/2 = 9°27′. Using the equations he had arrived at by his sequence of transformations, Kutta laboriously calculated the speed of the air and hence the pressure at
22 different points on the upper and lower surface of the wing, beginning at the leading edge and working back to the trailing edge. He assumed a flying speed of 10 m/sec, an atmospheric pressure of 760 mm of mercury, and an air temperature of 10° C. The results were drawn up in tabular form, and Kutta estimated that the lift would be about 10 kg per square meter of wing. This was the sort of result that would enable a wing of practical size to support a significant weight.

Kutta then addressed the practicalities of rounding the leading edge. How much should the front of the wing be thickened? What was the best geom­etry? Here Kutta felt the force of a dilemma. The suction force, which comes from the high speed of the flow, is important because it cuts down drag. The rounding therefore needs to be slight in order to keep up the speed so that the suction force is maintained. But it must not be too slight, otherwise, in reality, the flow will break down entirely, friction forces will take over, and the suction effect will be destroyed.

Der Erfolg ist somit, extrem gesprochen, dafi im Falle der fehlenden oder gar zu kleinen Abrundung die auf die Schale ausgeubte Auftriebskraft durch den Druckauftrieb allein gegeben ist, da die Saugwirkung fortfallt. (37)

The result, simply expressed, is that in the absence of a rounding [of the lead­ing edge] or with too small a rounding, the lift force operating on the curved surface will be provided by the pressure forces alone, because the suction ef­fect will have been removed.

He wanted a shape that would change the flow pattern as little as possible from those indicated by the mathematical analysis. For Kutta, the perfect, irrotational fluid flow represented an ideal that should be approached as closely as possible. Thus,

Wollen wir nur die negativen, physikalisch unzulassigen Drucke vermeiden, und gleichzeitig das Stromungsbild, and damit die Druckverhaltnisse in der Nahe des gefahrlichen Punktes A moglichst wenig andern, damit die fruhe – ren Formeln noch verwendbar bleiben, so werden wir die Kante parabolisch, namlich so wie die Stromungslinien bei A verlaufen, abrunden. (31)

If we want to avoid the physically impermissible pressures near the criti­cal point A [the leading edge], while at the same time altering the flow and pressure relations as little as possible, so that the previous formulas remain applicable, then we should make the edge parabolic, that is, like the stream­lines at A.

Using the analysis carried out in the previous section of the paper, and apply­ing it to various forms of leading edge shape (see fig. 6.5), Kutta reached the following conclusions. Given the 2 m chord of Lilienthal’s wing, the leading

edge should have a thickness of 12 cm. The greatest thickness should be about 12-16 cm from the leading edge itself and should merge with the arc of the wing some 40 -50 cm from the edge, that is, at about one-fourth of the chord (35). This, he concluded, would produce the optimum leading-edge suction. The surface friction and the vortices coming from the wingtips would still provide some drag, but these effects fell outside the scope of the assumptions he was making.

The formula given earlier linking the induced drag CDi to the lift CL led Prandtl to two further results that were significant for engineering and indicative of the power of the analysis he was developing. He discovered two practical formulas that allowed him to reduce drastically the amount of time spent conducting wind-channel tests. It allowed him to generalize results about in­duced drag and induced angle of incidence from a wing that had been tested to other wings with a different aspect ratio that had not been tested. All that was necessary was that the wings have the same cross-sectional profile. In this section I explain how Prandtl was able to do this.

The formula (deduced above) for the coefficient of induced drag, namely,

is analogous to the equation y = ax2, where y = CDi and x = CL, while a is the constant i/kAr. Equations having the form y = ax2 generate curves in the shape of a parabola. The constant a determines the curvature of the pa­rabola. According to Prandtl’s theory, then, the curve linking the coefficients of induced drag and lift will be parabolic, and the curvature will depend on the aspect ratio. Is this theoretical deduction confirmed experimentally? The “polar curves,” as Lilienthal called them, which link the observed coefficients of lift and drag are, indeed, roughly parabolic, but some distinctions need to be drawn before such results can be related to the parabolic formula for the induced drag.

Induced drag arises in an ideal fluid but also plays a role in real fluids. There are, however, other sources of drag that are present in real fluids. A real wing in real air will experience some degree of skin friction due to the viscos­ity of the air. As Betz had previously argued, the flow of air over a real wing will also generate eddies, and the flow over the upper and lower surfaces will not join together smoothly at the trailing edge. This, too, is a source of drag. Prandtl grouped both of these latter sources under the name “profile drag.” Thus the empirical phenomenon of drag is the combined effect of induced drag and profile drag. The empirical coefficient of drag can be understood as the sum of the coefficient of induced drag and the coefficient of profile drag. Thus, using obvious notation,

CD = CDi + CDp.

If the theoretical polar curve relating induced drag and lift is plotted on the same diagram as an empirical curve relating total drag to lift, it turns out that the curves are similar but not identical. They lie close to one another but do not overlap. Their relative position shows that most of the drag on the wing is induced drag. This is particularly true at high angles of incidence (see fig. 7.13).

Prandtl realized that the contingent relation between the two drag curves could be exploited. He spoke of a “fortunate circumstance that had not been suspected at all at the outset”—“einen glucklichen Umstand, der von vorn – herein keineswegs vermutet wurde.”75 It was a stroke of good fortune that al­lowed the results of his wing theory to be cast into a form that was highly use­ful for practical purposes (“gelang es nun, die Ergebnise der Tragflugeltheorie auch fur die Praxis noch wesentlich fruchtbarer zu gestalten”). As Prandtl explained:

Man trug namlich die Polarkurven bei sonst gleichen Tragflugeln, aber von verschiedenen Seitenverhaltnissen auf und erkannte, dafi der Unterschied der gemessenen Widerstandszahl von der theoretischen in allen Fallen nahezu der gleiche war. Daraus war zu schliefien, dafi der Profilwiderstand unab – hangig vom Seitenverhaltnis ist, woraus sich weiterhin die Moglichkeit ergab, gemessene Polarkurven von einem Seitenverhaltnis auf ein anderes Seitenver­haltnis umzurechnen. (219-20)

The polar curves of wings that are the same, apart from having different aspect ratios, were laid out, and one could see that the difference between the mea­sured and the theoretical resistance coefficient was approximately the same in all cases. It had to be concluded from this that the profile resistance was independent of the aspect ratio. This raised the possibility that the measured polar curve for one aspect ratio could be converted into that for another as­pect ratio.

Prandtl’s compressed reasoning can be broken down into two steps. First, the total drag is the sum of induced drag and profile drag (and the larger and more important of these two quantities is the induced drag). Second, if the profile drag CDp is roughly the same for wings of all aspect ratios, then the difference between total and induced drag would be the same if the wings were operating at the same coefficient of lift. In other words, the quantity ( CD – CD) would be a constant. This quantity could therefore be equated for wings of different aspect ratio, provided they both had the same profile and both had an elliptical lift distribution. The implication was that given two wings, wing(1) and wing(2), the total drag of wing(2) could be predicted once

it was known for wing(1). If the aspect ratios and the coefficients of total and induced drag for the respective wings are also distinguished by the labels (1) and (2), Prandtl was able to write

Q>(1) – CDI.(1) = Cd(2) – CDi(2).

It had already been established that

so this result could be substituted into the above equation to give

Rearranging the equation gives the drag of one wing in terms of the drag of the other, at the same value of the lift coefficient. The formula thus allows knowledge about one wing to be converted into knowledge about the other wing. The conversion formula was thus

П Li___ L_ I.

П і A (2) Ar (1))

A second conversion formula was then deduced. This formula dealt not with drag but with the angle of incidence. Once again it converted knowledge gained from one case into knowledge applicable to other cases. The second formula implied that if the angle of incidence associated with a given lift is known for a wing of one aspect ratio, then the angle at which that lift was pro­duced could be predicted for another wing of the same profile but a differ­ent aspect ratio. In this case the reasoning depended on the relation between finite wings and an infinite wing with the same profile.

Prandtl argued as follows. Suppose an infinite wing, of a given profile, meets a horizontal airstream at an angle a0. Let the lift coefficient be Cl. What would happen if this profile were to meet the air at the same speed but now as part of a finite wing, not an infinite wing? Prandtl had shown that the ef­fect of the vortices, which now trail from the tips, is to induce a downward flow of the air that presents itself to the wing. This induced angle ф reduces the effective angle of incidence of the wing. If the finite wing is to generate the same amount of lift per unit length as the infinite wing, then it must be restored to the same angle relative to the local flow that it originally had to the free stream. This can only be done if the angle to the horizontal is increased.

The angle of attack a will have to be made equal to the original angle a0 plus the induced angle of incidence ф. Thus, a = a0 + ф. Rearranging the equa­tion leads to a0 = a – ф. This expression implies that, for all wings of the same profile, the difference between the angle of attack and the angle of the induced flow will be the same when they are delivering the same amount of lift. Thus for two such wings, using obvious notation,

a0 = a1 – ф1 = a2 – ф2.

Suppose that wing(1) has the lift coefficient CL at a1 and wing(2) has the same lift coefficient at a2. Prandtl had already arrived at an expression for the in­duced angle of incidence ф, so he could write

C. 1 C. 1

a. = a. — —- = a — —- .

0 1 n Ar (1) 2 n Ar (2)

This gives the second conversion formula

Cl I 1 1 I

a=a +—I———— .

2 1 4 Ar (2) AR (1) J

If these two formulas stood up to test, they would fulfill the desiderata for work in technical mechanics identified by August Foppl. I described in chap­ter 5 how Foppl had insisted that the role of time in the economy of knowl­edge was different for the engineer compared to the physicist. The value of the conversion formulas was that they would enormously lighten the work load of the engineer engaged in wind-channel research.

The formulas were first published by Betz in 1917 in the confidential Tech – nische Berichte.76 They were then tested in Gottingen by taking wings of dif­ferent aspect ratios in order to see if the measurements for drag and angle of incidence could be converted into the values for one, arbitrarily chosen, aspect ratio. The first such test was performed by Munk and was also re­ported in the Technische Berichte71 Munk used just three different aspect ra­tios and, in order to keep the section of the wings as constant as possible, simply started with a long span of wing and sawed off the ends to produce the shorter wings. In this way he produced wings of aspect ratio 6, 5, and 4. Munk verified the formulas by calculating the results for the wing of aspect ratio 6 from the other two aerofoils and plotting the three sets of points in the same graph. Later the experiment was repeated with seven different aspect ratios and produced the same positive result. Except for the measurements taken on one wing of very low aspect ratio, the predictions worked well. The conversion formulas did what they were meant to do, that is, collapse all the experimental results into one and the same curve.78

Any direct test of the conversion formulas was also an indirect test of the theoretical assumptions on which they were based. As well as sanction­ing a practical shortcut that avoided much time-consuming work with the wind channel, the positive results of the test were a corroboration of Prandtl’s overall analysis. But all of the reasoning rested on the assumption that the lift distribution was elliptical. This facilitated the calculations but made the result a special case. Could the result be generalized? In November 1913 Prandtl and E. Pohlhausen had established that the induced drag for an el­liptical lift distribution was not only constant along the span but represented a minimum value.79 Any deviation from an elliptical distribution would give a higher value for this form of drag. It was also soon established that the actual planform that produced an elliptical lift distribution was itself of an elliptical shape. This was not because there is any simple rule to the effect that wings generate distributions that mirror the shape of their planform. In general, the shape of a wing does not immediately correspond to that of the resulting lift distribution. A rectangular wing does not yield a rectangular lift distribution. But, despite having the character of special case, it turned out that all the results derived for the elliptical wing could be generalized. The mathematical apparatus that has just been sketched could be applied, with­out significant loss of accuracy, to non-elliptical wings, for example, to the simple-to-construct rectangular wing that was used as the baseline or “norm” (the Normalflugmodell) in the Gottingen profile tests.80

The empirical basis for the generalization has already been mentioned. It rests on the “family resemblance” between the lift distributions of all typi­cal wings. Though their lift distributions are not strictly elliptical, they are, mostly, roughly elliptical. As Prandtl pointed out, while the true ellipse gives the minimum possible induced drag, many mathematical functions change their values slowly in the vicinity of a minimum. Results that hold for the minimum are often found to hold, at least approximately, in the neighbor­hood of the minimum.81 Thus the Gottingen results had a practical applica­bility, and a predictive power, that went beyond what might have been ex­pected, given the specialized, and often unreal, assumptions on which they were based. Looking back, some quarter of a century after the creation of Prandtl’s theory, Richard von Mises summed up the situation as follows: “It seems appropriate to stress the fact that. . . the parabolic form of the polar diagram and the dependence of this form on the aspect ratio, and the relation between lift coefficient, angle of attack, and aspect ratio, were not known as empirical facts before the wing theory was developed. These facts . . . have been predicted by the theory. Experiments carried out a posteriori have con­firmed these theoretical predictions to a degree that is remarkable in view of the numerous idealisations of the theory.”82 Von Mises was not a wholly unqualified admirer of the Gottingen group—he thought they cited one an­other too much—but the word “remarkable,” applied to the success of the Gottingen theory, was reiterated in his book Theory of Flight.83 The repetition attests to the striking and, it would seem, almost baffling power of Prandtl’s work. Let us look a little more closely at some of the methodological features that were associated with this success.

It was not until July 3, 1923 (after the confrontations at the Royal Aeronauti­cal Society and the International Air Congress), that the Aerodynamics Sub­Committee took a formal decision to test the Prandtl theory. The minutes read as follows: “That the investigation of the air flow behind aerofoils of finite and infinite span be carried out to ascertain how far the Prandtl theory of circulation can be substantiated by experiment.” The decision was passed to the full committee and ratified on July 10.13

After some delays the much-discussed experiment went ahead at the Na­tional Physical Laboratory. L. W. Bryant and D. H Williams performed a large number of measurements to build up a picture of the speed and direction of the air at points around a vertically positioned aerofoil that stretched across the full seven-foot depth of the NPL’s largest air channel. They did not use a Joukowsky aerofoil but a thick, high-lift section, chosen by Bairstow, that they positioned at approximately 10° to the air flow, which moved at about 49 feet per second. From a study of the velocity data it was possible to evaluate the circulation around various, selected contours. Some of these were cho­sen to loop round the wing itself, while some were closed contours that did not include the wing but were merely located in the space around it. If the flow was irrotational, the latter contours should yield a zero circulation. By contrast, according to the circulation theory, all contours enclosing the wing should show the same, nonzero circulation whose magnitude was related to the lift by the fundamental equation L = p VT. The lift was established by tak­ing pressure measurements. Inserting this empirical value for L in the equa­tion gave a predicted value for the circulation Г, which could be compared with the circulation computed from the velocity measurements.

In November 1923 the committee received Glauert’s technical report T. 1850 titled “Experimental Tests of the Vortex Theory of Aerofoils.”14 This was a general summary of evidence in support of Prandtl’s approach but began with a preliminary analysis that Glauert had made of data provided by Bryant and Williams. The measurements, carried out at what Glauert called a “rela­tively high angle of incidence,” enabled him to present a graph that showed the circulation plotted against the area of the contour around the wing along which the circulation had been measured. The graph indicated that the cir­culation was roughly independent of the area. Different-sized contours were indicating the same value for the circulation—just as the theory implied.

What is more, the numerical value of this circulation was almost exactly the value predicted from the formula. Things looked promising for the support­ers of the theory. There had yet to be any direct test of the zero circulation in the contours that did not enclose the wing, to check that the flow was indeed irrotational, but the indirect evidence gathered so far seemed to confirm the assumption of irrotational flow.

Taylor set about to show that this evidence was not as good as it looked. In January 1924, he submitted his “Note on the Prandtl Theory.”15 It was meant to block the inference that Glauert was making on the basis of the preliminary data. Taylor argued as follows. If the flow is irrotational, then all the contours around the wing will have the same circulation. This condition was consistent with the experimental results, but no experiment can test all contours and, so far, only a few had been checked. It does not follow that, because some con­tours show the same circulation, the flow must be irrotational. In the present case Taylor was convinced that the flow could not be irrotational. His suspi­cions were aroused by the use of a wing at high incidence, that is, approach­ing the stalling angle. Previous experiments had shown that the wing would be experiencing high resistance, although it should have zero resistance in an irrotational flow. The high resistance means the flow cannot be everywhere irrotational. There would be a significant wake, and the fluid elements in the wake would be rotating—some this way, some that. If the experimental read­ings showed that various contours all had the same circulation, then there must be something peculiar about the contours. “Mr. Glauert’s result would have to be attributed to a fortunate choice of his contour rather than to an irrotational type of flow” (3).

How could contours of different sizes exhibit the same circulation with­out this indicating the irrotational nature of the flow through which the con­tour had been drawn? Taylor gave an example to show how this result might arise. Imagine a wing profile surrounded by two circular contours, A and B, which have a common center on the wing. Both are large compared to the wing, but B has a greater radius than A. (See fig. 9.2, which is taken from Taylor’s report.) Suppose that the wing generates a wake with, say, positive vorticity issuing from the upper surface and negative vorticity from the lower surface. The wake is shown in the diagram contained between the dotted lines. The circulation around the circle A is, by Stokes’ theorem, equal to the total vorticity within the area enclosed by the contour. Here there will be two sources of vorticity: the vorticity along the surfaces of the wing and the vor – ticity provided by the wake. Now consider the circulation around the larger circle B. Any difference between the circulation around A and B must come from the vorticity in the wake that lies in the area between the two circles.

Taylor, however, was interested in the conditions that would make them have the same circulation, that is, the conditions that might lead the unwary into supposing that the contours passed through a flow that was wholly irrota­tional. Such a condition would arise if the amounts of positive and negative vorticity issued into the wake were equal. The flow would not be irrotational, but it would yield the same circulation for the different contours. The con­ditions of this example may be special, but they are sufficient to expose the fallacy of inferring the irrotational nature of the flow simply from the equality of circulation around a number of different contours.

This was the essence of Taylor’s argument but not the end of it. Glauert’s preliminary analysis of the experiment not only suggested that the circula­tion was the same on contours of different sizes, but it also revealed that the circulation’s magnitude was almost precisely that predicted from the basic law relating lift to density, speed, and circulation. Could that be explained by the unwitting selection of a “favorable” contour? Taylor showed that the answer to this question is yes. His argument was based on the equations that, respectively, express the conservation of momentum perpendicular to, and parallel to, the direction of motion of an aerofoil. Consider a body in a stream of fluid of velocity U parallel to the x-axis. Taylor wrote down, in what is now a standard way, the momentum flux equations across an arbitrary con­tour C which encloses the body. After some manipulation, and disregarding small quantities, he arrived at the following two expressions. One concerned the drag forces lying in the direction of motion; the other concerned the forces perpendicular to the motion and defined the relation between lift and circulation:

where D is drag, L is lift, U is the velocity of the free stream and I is the circulation, p is density, p is pressure, q is velocity, and m and l are direc­tion cosines. These indicate the slope of the contour. Thus m expresses the orientation of the contour at a given point by giving the cosine of the angle between the normal at that point and the y-axis, while l functions in the same way but gives the cosine of the angle between the normal and the x-axis. The expression in brackets, under the scope of the integral sign, is proportional to what is called the “total head” and (as explained in chap. 2) is a quantity measured by a Pitot tube facing the oncoming stream of air.16

For Taylor’s immediate purposes it was the second of these equations, dealing with the lift L, that was most important. The equation is obviously similar to the Kutta – Joukowsky equation. The familiar product of density, speed, and circulation (here expressed as p UI) is clearly visible, but with the addition of the integral on the right-hand side. Taylor drew attention to the following features of the equation. If the flow is irrotational, the expression in the brackets, the total head, is a constant, and as a result the value of the integral around the contour is zero. This removes the term from the equa­tion and leaves L = p UI, the basic law of lift. Thus the simple law follows from his analysis, given the assumption that the flow is irrotational. But sup­pose there is a wake. Within the wake the flow is not irrotational. Along the part of the contour that passes through the wake, the total head will not be a constant but will vary in magnitude. In general, under these conditions, the value of the integral will not be zero. The simple proportionality between lift and circulation will then no longer hold. But, Taylor noted, the bracket under the integral is multiplied by m, the direction cosine. If the contour is so chosen that the part of it that cuts the wake is perpendicular to the main flow, that is, perpendicular to the x-axis and parallel to the y-axis, then m will be zero. (The angle between the normal to the contour and y-axis will be 90°, and the cosine of 90° is zero.) This feature of the mathematics makes the integral zero once again. For such a contour, the integral term in the equa­tion will disappear and leave an expression that coincides with the simple law of lift.

It follows that one cannot infer that the flow is irrotational just because the data are related by the law L = pUI. Even though some of the flow is not irrotational, this relation between lift and circulation can hold because of the choice of the contour. Taylor summed up his argument in the following words: “We have now seen that the relation L = pUI may be expected to hold even when the motion is not irrotational provided that the circuit used in calculating I is chosen in a particular manner. If Mr. Glauert’s circuits are in fact chosen in this manner his result though interesting in itself cannot be re­garded as being in any sense confirmatory of Prandtl’s fundamental hypoth­esis that the motion at a great distance from the aerofoil is irrotational” (7).

Taylor’s deduction depended on neglecting small quantities. To justify this step he had assumed that the disturbances caused by the aerofoil declined as l/R, where R is the distance from the aerofoil. Taylor was conscious that this step might hide a problem for his argument. Could the l/R assumption be tantamount to admitting that the flow was irrotational? Taylor seemed un­sure but circumvented the problem by showing that there were other coun­terexamples that would block Glauert’s inference, and these did not depend on the l/R assumption.

Here Taylor produced his piece de resistance. He reanalyzed Rayleigh’s 1876 paper on discontinuous flow around an inclined plate and showed that the circulation in the flow conformed to the law L = pUI, provided the con­tour cut the dead air of the wake perpendicular to the direction of the main motion. (See the contour marked C’ in fig. 9.3, again taken from Taylor’s report.)

Rayleigh flow clearly bears no resemblance to the flow assumed by Prandtl. Although the relevant integral can be specified, the idea that Ray­leigh flow has a “circulation” is not physically well defined because there is no unique value attributable to it. The value will depend on the contour. This was Taylor’s point. With the “right” sort of contour, he was able to show that the value of the integral will tend to the same limit, L/p U, as that derived from the assumption of an irrotational flow with circulation. Armed with these remarkable results Taylor drew his final conclusion: “It appears, there­fore, that if Mr. Glauert’s contours were taken in the special way described his results would be expected whatever the type of flow round the aerofoil may

be. It cannot be taken as confirmation of Prandtl’s hypothesis” (14). Were “Mr. Glauert’s contours” taken in this way? Were they perpendicular to the main flow where they cut the wake? The answer is yes. Bryant and Williams had used just such contours to establish the circulation around the wing, and those were the ones Glauert employed in his preliminary analysis. Taylor had pulled the rug from beneath Glauert’s feet.

Despite Taylor’s criticisms, Bryant and Williams’ experiment was written up as a technical report (T. 1885) in February 1924.17 It was eventually pub­lished, in an expanded form, in the Philosophical Transactions of the Royal Society in 1926 along with an appendix from Taylor.18 Taylor’s appendix gave essentially the same mathematical and methodological argument as his “Note on the Prandtl Theory,” described earlier. The combination of paper and ap­pendix makes uncomfortable reading because no attempt had been made to modify the contours in the light of Taylor’s comments. The only significant differences between the original technical reports presented to the Research Committee and the published papers lay in the tone of Taylor’s contribution. He had made two alterations. First, the published version contained none of the sharp words directed at Glauert. Second, Taylor chose to reformulate his methodological point and express it in different words. Instead of saying that the purpose of his argument was to show what type of contour should not be used, Taylor now said his purpose was to show what sort must be used if, that is, one desires to get the result that L = pUI for a flow that is not irrota- tional. Thus, “the object of the present note is to find out which type of con­tour must be chosen in order that the lift-circulation relation may be satisfied when the motion is not irrotational” (238).

Logically, this declaration is equivalent to what Taylor said to Glauert, but it is no longer framed as an objection. In the unpublished note Taylor had uncompromisingly stated that the result of the experiment “cannot be taken as confirmation of Prandtl’s hypothesis.” In the published appendix his conclusion was reexpressed as follows: “The relationship between lift and cir­culation may hold when the motion is not even approximately irrotational, provided that large contours are chosen so that they cut the wake in a straight line perpendicular to the direction of motion of the aerofoil” (245).

An anonymous report in Nature, commenting on the published account of the experiment, correctly summarized the position and noted that Bryant and Williams had used contours of a special type, “so that the accuracy with which the observed lift force agrees with that predicted from measurements of circulation is no indication that the flow is in fact an irrotational motion with circulation.”19 Although Nature got it right, it is not surprising, given the rewording, that the significance of Taylor’s note sometimes proved elusive. For example, von Karman and Burgers, writing in 1935 in their chapter in Durand’s Aerodynamic Theory, appeared to miss this point.20 They correctly noted that, when the contour cuts the wake at right angles, “then the value of the circulation is the same for all curves under consideration” (8). But they went on: “If the condition that the line must cut the wake at right angles were not stipulated, the magnitude of the circulation would become indefinite, as an arbitrary number of vortices, ‘washed out’ from the boundary layers along the surfaces of the aerofoil, and rotating either in one sense or in the other, could be included. The necessity of this condition was pointed out by G. I. Taylor”(8). This is true, but it turns the original argument on its head. What Taylor had sought to prohibit has now become a stipulation.21

If Haldane had not followed the advice of a Trinity mathematician when he set up the Advisory Committee for Aeronautics but had, say, recruited Cam­bridge engineers rather than mathematical physicists, he might have got a very different committee. In principle he could have done this because Cambridge had a distinguished school of engineering.25 Predictably, there had always been a tension between the demands of a practical engineering education and the demands of the traditional, Cambridge mathematical curriculum. There was not time in the day to succeed at both, except for the outstanding few. It was not until 1906 that a satisfactory accommodation was reached when Bertram Hopkinson, the professor of mechanism and applied mechanics, gave a viable and independent structure to the Mechanical Sciences Tripos. This took the engineers out of the competitive hothouse, though inevitably it meant they operated at a somewhat less sophisticated mathematical level. The products of Hopkinson’s department played a distinguished role in the development of British aeronautics. Busk (who made the BE2 stable), Farren (who championed full-scale research at Farnborough), Melvill Jones (who worked on low-speed control and gunnery), Southwell (who worked on air­ship structures), and McKinnon Wood (the experimentalist who went with Glauert to see Prandtl) were all products of the Cambridge school of engi­neering. Hopkinson himself, though of an older generation, learned to fly during the Great War and did important work on aircraft testing at Martle – sham Heath. He met his death at the controls of a Bristol Fighter in a flying accident in August 1918.26

Perhaps a counterfactual Advisory Committee, made up of men like Ber­tram Hopkinson, would have embraced Lanchester and the circulatory the­ory. This is consistent with my analysis, although the conclusion would only follow if Cambridge engineers were significantly different in their judgments and orientation from their Mathematical Tripos colleagues and significantly similar to the German engineers from Gottingen and Aachen. Such a premise is plausible but it cannot be taken for granted, and there is some evidence that calls it into question. In certain respects Cambridge engineers adopted atti­tudes that were similar to those of the more traditionally trained mathemati­cians. This is not surprising in the case of the older products of the Cambridge school of engineering because they too were steeped in the earlier Mathemati­cal Tripos tradition. Bertram Hopkinson’s father, John Hopkinson, had been both an engineer and a senior wrangler. After a fellowship at Trinity he be­come a professional, consulting engineer in London but retained a strongly mathematical bent. He developed a mathematical analysis of the alternating current generator and predicted that it should be possible to run such genera­tors in parallel. Practical engineers knew that, given the available machines, they could not be run in parallel, but none of this blunted the confidence of the mathematically able Hopkinson.27 Bertram Hopkinson himself had also read for the Mathematical Tripos and had been a highly placed wrangler. Al­though more practically inclined than his father, he had worked on topics in hydrodynamics and had written a paper on the theory of discontinuous flow.

He extended the work of A. E. H. Love by making allowance for the presence of sources and vortices.28 None of those who contributed to the mathematical development of the theory of discontinuous flow ever went on to work on the mathematics of the circulation theory of lift.

What about the somewhat younger generation of Cambridge engineers such as Busk, Farren, Melvill Jones, McKinnon Wood, and Southwell? Here, too, the evidence indicates that, although they had some sympathy with Lanchester, that sympathy had its limits. And those limits were character­istic of the milieu of Cambridge mathematical physics. Southwell’s role as a lecturer in mathematics at Cambridge (despite his engineering background), and his commitment to a fundamental physics of lift, have already been de­scribed. McKinnon Wood was perhaps different. He had come round quickly to the side of the Lanchester-Prandtl theory of circulation, though exactly why is unclear. It is possible that he was taking his lead from Glauert. Writing retrospectively, McKinnon Wood recalled that, as a student, he had borrowed Lanchester’s Aerodynamics from the Union library but then, after reading it, had thought no more about it.29 Looking back, all that he could report was re­gret at this “mysterious blindness.” Farren appears to have accepted a version of Glazebrook’s excuse and recalled Lanchester as an almost a tragic figure. He was a man who had clear insights but who could not give them expres­sion. “The vision of Lanchester brooding over the irony of a world which at last understood what he had seen so clearly, but had been unable to explain, will not fade from the minds of those who knew him.”30

Bennett Melvill Jones sought to shed light on these mysteries in a talk he gave at the Royal Aircraft Establishment at Farnborough in 1957.31 He de­scribed how, as a young man, his friend and fellow engineering student at Cambridge, Edward Busk, had introduced him to Lanchester’s work. It had deeply impressed them. After studying Lanchester’s treatise, “Ted and I sol­emnly decided to spend the rest of our lives on aeronautics.” But, Melvill Jones went on, aeronautics in Britain had then developed in an almost en­tirely empirical fashion, that is, without the guidance of Lanchester’s theory. This may seem surprising, he told his audience, “because the theory of ideal fluid, which now forms the basis of all your work, had already been very fully developed by Lamb and others. But in this theory, no body which starts from rest can, when in steady motion, experience any reaction whatever. And to us, whose business it was to study this reaction, this did not seem very helpful.” The source of the trouble, he explained, was the impossibility of accounting for the origin of circulation. This was the very same objection that the young G. I. Taylor had used against Lanchester in 1914. The origin of the circulation and hence the lift could not be deduced within the terms of the theory. If

Melvill Jones’ recollections were correct, then the products of the Mechani­cal Sciences Tripos had been at one on this question with the products of the Mathematical Tripos. Both saw its dependence on the classical hydrodynam­ics of potential flow as a fatal objection to Lanchester’s approach.

Melvill Jones went on to say that now (that is, by 1957) it may seem obvi­ous how this difficulty should have been resolved. He added, ruefully, that perhaps he and his contemporaries had not been very clever in making the response they did, but, he insisted, “our view was, at that time, shared by all engineers.” Here Melvill Jones was making a historical mistake. Even if the negative reaction to ideal fluid theory was shared by all Cambridge aeronau­tical engineers of his generation, or even by all British engineers, the response was not shared by the German engineers who developed the circulatory theory. In an attempt to justify the negative reaction to Lanchester, Melvill Jones said that the theory of ideal fluids, then known as hydrodynamics, “was regarded purely as an exercise for the amusement of students.” Again, while this may have been true in Cambridge it was not how things were seen in Gottingen or Aachen. This is not how ideal fluid theory was regarded by Betz, Blumenthal, Foppl, Fuhrmann, von Karman, Kutta, von Mises, Prandtl, or Trefftz. For them it was more than a source of ingenious examination ques­tions; it was a serious instrument of research and a serious technique with which to gain some purchase on reality.

The Cambridge ethos seems to have enveloped its engineers as well as its mathematicians. It therefore cannot be assumed that a counterfactual committee of Cambridge engineers would have responded as the German engineers did and welcomed the circulatory theory.32 This answer obviously depends on the range of factors that are allowed into the imaginary picture. If engineers had been given a dominant position on the ACA, they might have gained greater independence of mind. They might then have been less influ­enced than they actually were by the older Tripos tradition of mathematical physics. No one can know. The fact remains that these were not the men who initiated the research program into the theory of lift, and they did not have a dominant role on the committee that Haldane actually created.33