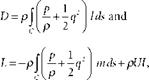The Experiment of Bryant and Williams

It was not until July 3, 1923 (after the confrontations at the Royal Aeronauti­cal Society and the International Air Congress), that the Aerodynamics Sub­Committee took a formal decision to test the Prandtl theory. The minutes read as follows: “That the investigation of the air flow behind aerofoils of finite and infinite span be carried out to ascertain how far the Prandtl theory of circulation can be substantiated by experiment.” The decision was passed to the full committee and ratified on July 10.13

After some delays the much-discussed experiment went ahead at the Na­tional Physical Laboratory. L. W. Bryant and D. H Williams performed a large number of measurements to build up a picture of the speed and direction of the air at points around a vertically positioned aerofoil that stretched across the full seven-foot depth of the NPL’s largest air channel. They did not use a Joukowsky aerofoil but a thick, high-lift section, chosen by Bairstow, that they positioned at approximately 10° to the air flow, which moved at about 49 feet per second. From a study of the velocity data it was possible to evaluate the circulation around various, selected contours. Some of these were cho­sen to loop round the wing itself, while some were closed contours that did not include the wing but were merely located in the space around it. If the flow was irrotational, the latter contours should yield a zero circulation. By contrast, according to the circulation theory, all contours enclosing the wing should show the same, nonzero circulation whose magnitude was related to the lift by the fundamental equation L = p VT. The lift was established by tak­ing pressure measurements. Inserting this empirical value for L in the equa­tion gave a predicted value for the circulation Г, which could be compared with the circulation computed from the velocity measurements.

In November 1923 the committee received Glauert’s technical report T. 1850 titled “Experimental Tests of the Vortex Theory of Aerofoils.”14 This was a general summary of evidence in support of Prandtl’s approach but began with a preliminary analysis that Glauert had made of data provided by Bryant and Williams. The measurements, carried out at what Glauert called a “rela­tively high angle of incidence,” enabled him to present a graph that showed the circulation plotted against the area of the contour around the wing along which the circulation had been measured. The graph indicated that the cir­culation was roughly independent of the area. Different-sized contours were indicating the same value for the circulation—just as the theory implied.

What is more, the numerical value of this circulation was almost exactly the value predicted from the formula. Things looked promising for the support­ers of the theory. There had yet to be any direct test of the zero circulation in the contours that did not enclose the wing, to check that the flow was indeed irrotational, but the indirect evidence gathered so far seemed to confirm the assumption of irrotational flow.

Taylor set about to show that this evidence was not as good as it looked. In January 1924, he submitted his “Note on the Prandtl Theory.”15 It was meant to block the inference that Glauert was making on the basis of the preliminary data. Taylor argued as follows. If the flow is irrotational, then all the contours around the wing will have the same circulation. This condition was consistent with the experimental results, but no experiment can test all contours and, so far, only a few had been checked. It does not follow that, because some con­tours show the same circulation, the flow must be irrotational. In the present case Taylor was convinced that the flow could not be irrotational. His suspi­cions were aroused by the use of a wing at high incidence, that is, approach­ing the stalling angle. Previous experiments had shown that the wing would be experiencing high resistance, although it should have zero resistance in an irrotational flow. The high resistance means the flow cannot be everywhere irrotational. There would be a significant wake, and the fluid elements in the wake would be rotating—some this way, some that. If the experimental read­ings showed that various contours all had the same circulation, then there must be something peculiar about the contours. “Mr. Glauert’s result would have to be attributed to a fortunate choice of his contour rather than to an irrotational type of flow” (3).

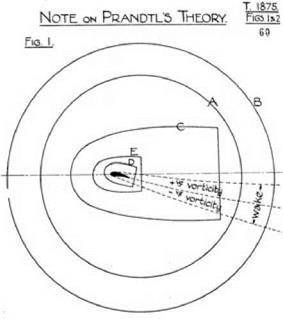
How could contours of different sizes exhibit the same circulation with­out this indicating the irrotational nature of the flow through which the con­tour had been drawn? Taylor gave an example to show how this result might arise. Imagine a wing profile surrounded by two circular contours, A and B, which have a common center on the wing. Both are large compared to the wing, but B has a greater radius than A. (See fig. 9.2, which is taken from Taylor’s report.) Suppose that the wing generates a wake with, say, positive vorticity issuing from the upper surface and negative vorticity from the lower surface. The wake is shown in the diagram contained between the dotted lines. The circulation around the circle A is, by Stokes’ theorem, equal to the total vorticity within the area enclosed by the contour. Here there will be two sources of vorticity: the vorticity along the surfaces of the wing and the vor – ticity provided by the wake. Now consider the circulation around the larger circle B. Any difference between the circulation around A and B must come from the vorticity in the wake that lies in the area between the two circles.

figure 9.2. G. I. Taylors counterexample to the conclusion drawn from Bryant and Williams experi­ment. Circulation around contour B is the same as around contour A, if equal amounts of positive and negative vorticity are generated by the wing. The irrotational character of a flow cannot be deduced from the sameness of circulation around a number of different contours. From ARC Technical Report 1875. (By permission of the National Archives of the UK, ref. DSIR 23/1889)

Taylor, however, was interested in the conditions that would make them have the same circulation, that is, the conditions that might lead the unwary into supposing that the contours passed through a flow that was wholly irrota­tional. Such a condition would arise if the amounts of positive and negative vorticity issued into the wake were equal. The flow would not be irrotational, but it would yield the same circulation for the different contours. The con­ditions of this example may be special, but they are sufficient to expose the fallacy of inferring the irrotational nature of the flow simply from the equality of circulation around a number of different contours.

This was the essence of Taylor’s argument but not the end of it. Glauert’s preliminary analysis of the experiment not only suggested that the circula­tion was the same on contours of different sizes, but it also revealed that the circulation’s magnitude was almost precisely that predicted from the basic law relating lift to density, speed, and circulation. Could that be explained by the unwitting selection of a “favorable” contour? Taylor showed that the answer to this question is yes. His argument was based on the equations that, respectively, express the conservation of momentum perpendicular to, and parallel to, the direction of motion of an aerofoil. Consider a body in a stream of fluid of velocity U parallel to the x-axis. Taylor wrote down, in what is now a standard way, the momentum flux equations across an arbitrary con­tour C which encloses the body. After some manipulation, and disregarding small quantities, he arrived at the following two expressions. One concerned the drag forces lying in the direction of motion; the other concerned the forces perpendicular to the motion and defined the relation between lift and circulation:

where D is drag, L is lift, U is the velocity of the free stream and I is the circulation, p is density, p is pressure, q is velocity, and m and l are direc­tion cosines. These indicate the slope of the contour. Thus m expresses the orientation of the contour at a given point by giving the cosine of the angle between the normal at that point and the y-axis, while l functions in the same way but gives the cosine of the angle between the normal and the x-axis. The expression in brackets, under the scope of the integral sign, is proportional to what is called the “total head” and (as explained in chap. 2) is a quantity measured by a Pitot tube facing the oncoming stream of air.16

For Taylor’s immediate purposes it was the second of these equations, dealing with the lift L, that was most important. The equation is obviously similar to the Kutta – Joukowsky equation. The familiar product of density, speed, and circulation (here expressed as p UI) is clearly visible, but with the addition of the integral on the right-hand side. Taylor drew attention to the following features of the equation. If the flow is irrotational, the expression in the brackets, the total head, is a constant, and as a result the value of the integral around the contour is zero. This removes the term from the equa­tion and leaves L = p UI, the basic law of lift. Thus the simple law follows from his analysis, given the assumption that the flow is irrotational. But sup­pose there is a wake. Within the wake the flow is not irrotational. Along the part of the contour that passes through the wake, the total head will not be a constant but will vary in magnitude. In general, under these conditions, the value of the integral will not be zero. The simple proportionality between lift and circulation will then no longer hold. But, Taylor noted, the bracket under the integral is multiplied by m, the direction cosine. If the contour is so chosen that the part of it that cuts the wake is perpendicular to the main flow, that is, perpendicular to the x-axis and parallel to the y-axis, then m will be zero. (The angle between the normal to the contour and y-axis will be 90°, and the cosine of 90° is zero.) This feature of the mathematics makes the integral zero once again. For such a contour, the integral term in the equa­tion will disappear and leave an expression that coincides with the simple law of lift.

It follows that one cannot infer that the flow is irrotational just because the data are related by the law L = pUI. Even though some of the flow is not irrotational, this relation between lift and circulation can hold because of the choice of the contour. Taylor summed up his argument in the following words: “We have now seen that the relation L = pUI may be expected to hold even when the motion is not irrotational provided that the circuit used in calculating I is chosen in a particular manner. If Mr. Glauert’s circuits are in fact chosen in this manner his result though interesting in itself cannot be re­garded as being in any sense confirmatory of Prandtl’s fundamental hypoth­esis that the motion at a great distance from the aerofoil is irrotational” (7).

Taylor’s deduction depended on neglecting small quantities. To justify this step he had assumed that the disturbances caused by the aerofoil declined as l/R, where R is the distance from the aerofoil. Taylor was conscious that this step might hide a problem for his argument. Could the l/R assumption be tantamount to admitting that the flow was irrotational? Taylor seemed un­sure but circumvented the problem by showing that there were other coun­terexamples that would block Glauert’s inference, and these did not depend on the l/R assumption.

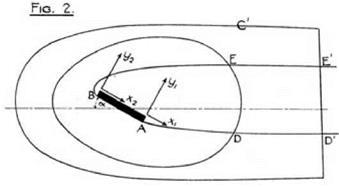
Here Taylor produced his piece de resistance. He reanalyzed Rayleigh’s 1876 paper on discontinuous flow around an inclined plate and showed that the circulation in the flow conformed to the law L = pUI, provided the con­tour cut the dead air of the wake perpendicular to the direction of the main motion. (See the contour marked C’ in fig. 9.3, again taken from Taylor’s report.)

Rayleigh flow clearly bears no resemblance to the flow assumed by Prandtl. Although the relevant integral can be specified, the idea that Ray­leigh flow has a “circulation” is not physically well defined because there is no unique value attributable to it. The value will depend on the contour. This was Taylor’s point. With the “right” sort of contour, he was able to show that the value of the integral will tend to the same limit, L/p U, as that derived from the assumption of an irrotational flow with circulation. Armed with these remarkable results Taylor drew his final conclusion: “It appears, there­fore, that if Mr. Glauert’s contours were taken in the special way described his results would be expected whatever the type of flow round the aerofoil may

figure 9.3. Taylor’s reanalysis of Rayleigh flow. The circulation around contour C’ conforms to the Kutta-Joukowsky law of lift, L = p U Г. Note that the contour cuts the wake of “dead” air at right angles. From ARC Technical Report 1875. (By permission of the National Archives of the UK, ref. DSIR 23/1889)

be. It cannot be taken as confirmation of Prandtl’s hypothesis” (14). Were “Mr. Glauert’s contours” taken in this way? Were they perpendicular to the main flow where they cut the wake? The answer is yes. Bryant and Williams had used just such contours to establish the circulation around the wing, and those were the ones Glauert employed in his preliminary analysis. Taylor had pulled the rug from beneath Glauert’s feet.

Despite Taylor’s criticisms, Bryant and Williams’ experiment was written up as a technical report (T. 1885) in February 1924.17 It was eventually pub­lished, in an expanded form, in the Philosophical Transactions of the Royal Society in 1926 along with an appendix from Taylor.18 Taylor’s appendix gave essentially the same mathematical and methodological argument as his “Note on the Prandtl Theory,” described earlier. The combination of paper and ap­pendix makes uncomfortable reading because no attempt had been made to modify the contours in the light of Taylor’s comments. The only significant differences between the original technical reports presented to the Research Committee and the published papers lay in the tone of Taylor’s contribution. He had made two alterations. First, the published version contained none of the sharp words directed at Glauert. Second, Taylor chose to reformulate his methodological point and express it in different words. Instead of saying that the purpose of his argument was to show what type of contour should not be used, Taylor now said his purpose was to show what sort must be used if, that is, one desires to get the result that L = pUI for a flow that is not irrota- tional. Thus, “the object of the present note is to find out which type of con­tour must be chosen in order that the lift-circulation relation may be satisfied when the motion is not irrotational” (238).

Logically, this declaration is equivalent to what Taylor said to Glauert, but it is no longer framed as an objection. In the unpublished note Taylor had uncompromisingly stated that the result of the experiment “cannot be taken as confirmation of Prandtl’s hypothesis.” In the published appendix his conclusion was reexpressed as follows: “The relationship between lift and cir­culation may hold when the motion is not even approximately irrotational, provided that large contours are chosen so that they cut the wake in a straight line perpendicular to the direction of motion of the aerofoil” (245).

An anonymous report in Nature, commenting on the published account of the experiment, correctly summarized the position and noted that Bryant and Williams had used contours of a special type, “so that the accuracy with which the observed lift force agrees with that predicted from measurements of circulation is no indication that the flow is in fact an irrotational motion with circulation.”19 Although Nature got it right, it is not surprising, given the rewording, that the significance of Taylor’s note sometimes proved elusive. For example, von Karman and Burgers, writing in 1935 in their chapter in Durand’s Aerodynamic Theory, appeared to miss this point.20 They correctly noted that, when the contour cuts the wake at right angles, “then the value of the circulation is the same for all curves under consideration” (8). But they went on: “If the condition that the line must cut the wake at right angles were not stipulated, the magnitude of the circulation would become indefinite, as an arbitrary number of vortices, ‘washed out’ from the boundary layers along the surfaces of the aerofoil, and rotating either in one sense or in the other, could be included. The necessity of this condition was pointed out by G. I. Taylor”(8). This is true, but it turns the original argument on its head. What Taylor had sought to prohibit has now become a stipulation.21