Section v. a numerical example:. rounding the leading edge

Kutta did not see leading-edge suction as calling for a purely mathematical investigation into a singular point in the equations of flow. He took it as an indicator of a practical problem. It pointed to the presence of high speeds that were physically real and which would result in the breakdown of the flow at the leading edge and the onset of turbulence. It pointed to the presence of vortices and other physical complexities. He therefore looked for an en­gineering solution by rounding off the leading edge, that is, by the provision of a thickening of the wing at the front which could then be shaped so as to prevent the breakdown of the flow. Here Kutta’s mathematics began to make direct contact with the practicalities of building an aircraft wing.

First, he made a rough numerical estimate of the lift of Lilienthal’s wing by inserting its specifications into his equations. The wing was an arc subtend­ing an angle of 2a = 37°50/ and having a curvature giving a maximum height of 1/12 of the chord length. The angle of attack в was set at в = a/2 = 9°27′. Using the equations he had arrived at by his sequence of transformations, Kutta laboriously calculated the speed of the air and hence the pressure at
22 different points on the upper and lower surface of the wing, beginning at the leading edge and working back to the trailing edge. He assumed a flying speed of 10 m/sec, an atmospheric pressure of 760 mm of mercury, and an air temperature of 10° C. The results were drawn up in tabular form, and Kutta estimated that the lift would be about 10 kg per square meter of wing. This was the sort of result that would enable a wing of practical size to support a significant weight.

Kutta then addressed the practicalities of rounding the leading edge. How much should the front of the wing be thickened? What was the best geom­etry? Here Kutta felt the force of a dilemma. The suction force, which comes from the high speed of the flow, is important because it cuts down drag. The rounding therefore needs to be slight in order to keep up the speed so that the suction force is maintained. But it must not be too slight, otherwise, in reality, the flow will break down entirely, friction forces will take over, and the suction effect will be destroyed.

Der Erfolg ist somit, extrem gesprochen, dafi im Falle der fehlenden oder gar zu kleinen Abrundung die auf die Schale ausgeubte Auftriebskraft durch den Druckauftrieb allein gegeben ist, da die Saugwirkung fortfallt. (37)

The result, simply expressed, is that in the absence of a rounding [of the lead­ing edge] or with too small a rounding, the lift force operating on the curved surface will be provided by the pressure forces alone, because the suction ef­fect will have been removed.

He wanted a shape that would change the flow pattern as little as possible from those indicated by the mathematical analysis. For Kutta, the perfect, irrotational fluid flow represented an ideal that should be approached as closely as possible. Thus,

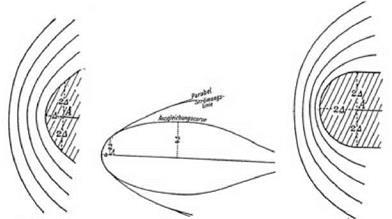
Wollen wir nur die negativen, physikalisch unzulassigen Drucke vermeiden, und gleichzeitig das Stromungsbild, and damit die Druckverhaltnisse in der Nahe des gefahrlichen Punktes A moglichst wenig andern, damit die fruhe – ren Formeln noch verwendbar bleiben, so werden wir die Kante parabolisch, namlich so wie die Stromungslinien bei A verlaufen, abrunden. (31)

If we want to avoid the physically impermissible pressures near the criti­cal point A [the leading edge], while at the same time altering the flow and pressure relations as little as possible, so that the previous formulas remain applicable, then we should make the edge parabolic, that is, like the stream­lines at A.

Using the analysis carried out in the previous section of the paper, and apply­ing it to various forms of leading edge shape (see fig. 6.5), Kutta reached the following conclusions. Given the 2 m chord of Lilienthal’s wing, the leading

edge should have a thickness of 12 cm. The greatest thickness should be about 12-16 cm from the leading edge itself and should merge with the arc of the wing some 40 -50 cm from the edge, that is, at about one-fourth of the chord (35). This, he concluded, would produce the optimum leading-edge suction. The surface friction and the vortices coming from the wingtips would still provide some drag, but these effects fell outside the scope of the assumptions he was making.