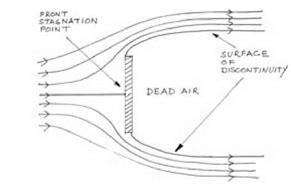
In 1910 the Society of German Aeronautical Engineers began to publish the Zeitschrift fur Flugtechnik und Motorluftschiffahrt—the journal for aeronautics and motorized airship transport.45 The ZFM, as it was called, rapidly became the leading scientific publication in the field. There was no precise British equivalent. The ZFM was more technical than, say, the Aeroplane or Flight and yet more accessible, and certainly more diverse, than the Reports and Memoranda of the Advisory Committee for Aeronautics. As well as scientific reports it contained general survey articles on the state of aviation, accounts of the latest exhibitions and meetings, and reviews of recent publications. There was, however, no close reporting of political controversies of the kind that was conspicuous in the British aeronautical press. Perhaps the nearest British publication was the Journal of the Aeronautical Society, but unlike the ZFM, this was not a routine vehicle for publishing research results.46 The lack of any British equivalent hints at the different ways aeronautical knowledge was integrated into the institutions of the two countries. Those who wrote for the ZFM communicated across boundaries between theorists and practitioners that seemed more difficult to overcome in Britain, while their silence in the domain of politics shows that there were other boundaries that remained higher in Germany than in Britain.
The advisory board of the ZFM was impressive. The journal was edited by the Berlin engineer Ansbert Vorreiter, and the scientific side was under the guidance of Ludwig Prandtl in Gottingen. Alongside Prandtl the board contained Carl Runge, also of Gottingen, along with Finsterwalder of the TH in Munich, Reissner of the TH in Aachen, and von Parseval and Bendemann from the TH in Charlottenburg. The masthead of the journal also carried the name of Dr. N. Joukowsky. His affiliation was given as the University of Moscow and the technische Hochschule of Moscow.
In the issue of November 26, 1910, the ZFM published the first part of a two-part article by Joukowsky titled “Uber die Konturen der Tragflachen der Drachenflieger” (On the shape of the wings of aircraft).47 The article has come to occupy a notable position in the history of aerodynamics. It is cited as the source of an important methodological shift in the mathematics of lift. The shift consisted in replacing Kutta’s complicated conformal transformations with a single, simple transformation, now called the Joukowsky transformation. Not only was it simpler, but it produced a more realistic aerofoil shape. Kutta’s method had merely produced a geometrical arc. The arc was an adequate model of Lilienthal’s wing, but it did not capture the increasing use of wings with a rounded, rather than sharp, leading edge as well as a slender tailing edge. Kutta had established the logic of the process by which knowledge of the flow around a circular cylinder could be turned into knowledge about the flow around a wing. The next step was to refine and improve this method of analysis. It is in this connection that Joukowsky’s paper has, rightly, achieved the status of a classic.
A reader who is aware of its reputation, but who confronts Joukowsky’s paper with fresh eyes, might feel puzzled. Where is the bold simplifying stroke? The inner coherence of the mathematics of the infinite wing, so evident in the textbooks that emerged a few years later, is not to be seen. The argument of the paper lacked clarity, and Joukowsky cited formulas without proof and used them without adequate explanation. There was also an edgy concern with issues of priority, particularly Russian priority, and some distracting typographical errors. The formula in the theory of complex variables that is now called the Joukowsky transformation was not actually stated in the paper, although some of its immediate consequences were given a limited application. But any inclination toward disappointment should be resisted. The smoothness of the later analysis is indeed absent from the paper, but that is because the later analysis was the work of others who learnt from Joukowsky and carried his ideas further. It was a collective, not an individual, accomplishment.
What was Joukowsky’s own contribution? I answer this question by giving an analysis of the argument of the 1910 paper. Joukowsky began by stating, without proof, two formulas for the lift, P, of an aerofoil that takes the form of a circular arc. The first was for an arc at zero angle of incidence; the second was for an arc at the arbitrary angle of incidence p. The formulas were
2 a 2 P = 4na sin— pV 2
and
P = 4na sin—sin+ pV2>
where V is the free stream velocity, p the density, a the radius of the circular arc, and a is specified as half the angle subtended by the arc at the center of the circle. Clearly, the two expressions become the same when P = 0. Kutta published both of these formulas, the first, simpler one in 1902 and the second, more general one in 1910, the same year as Joukowsky’s paper.48 Joukowsky, however, said that his colleague Sergei Tschapligin had by this time already discovered the second formula.49
Next came a discussion of the general lift theorem L = p V Г. Here a full proof was provided. Joukowsky approached the problem in terms of the flow of momentum across a control surface. His proof was of a type that has now become standard in modern textbooks. Again, Joukowsky raised issues of priority. He allowed that Kutta discovered this theorem in his unpublished thesis of 1902 but pointed out that he, Joukowsky, in 1906, was the first to publish it.50 He also noted that Finsterwalder had accepted this priority claim.51 Joukowsky granted that Lanchester had been the first to explain the relation between two-dimensional and three-dimensional flow by introducing the trailing vortices. At this point the main business of the paper was announced. In studying the problems of Kutta flow, said Joukowsky, he had found contours of a winglike form (“von flugelartiger Form”) that did not, like Kutta’s arc-wing, give rise to infinite velocities at the leading edge. The aim of the paper was to show how to construct these contours and to test their properties empirically:
Die Beschreibung der Konstruktion dieser Konturen und die experimentelle Untersuchung der ihnen entsprechenden Widerstandskrafte der Flussigkeit stellt den Inhalt dieser Arbeit dar. (283)
The content of the work can be represented as the description of the construction of these contours and the experimental study of the corresponding resistance forces of the fluid.
Joukowsky set out, step by step, a geometrical procedure for transforming a circle into the first of his two contours. Whereas Kutta had employed functions of a complex variable, Joukowsky took his readers back to the geometry lessons of the classroom. The procedure involved drawing circles and tangents, labeling significant points and angles in the figure, carrying out some careful measurements on the diagram, and then adding construction lines. To start the process, said Joukowsky, it is necessary to draw a circle whose center is labeled O and whose radius is a. Some arbitrary point E is then chosen which lies outside the circle, and from E two tangents are drawn. The angle enclosed by the tangents at E is called 2a. It is then required to draw a second, larger circle whose radius is called b. The larger circle does not share the same center O as the smaller circle. Rather, its position is determined by the requirement that it encloses the smaller circle but touches it so that it shares one of the tangents. It is this larger circle that is to be transformed into the aerofoil.
The next step was the addition of construction lines. These are needed to connect any specified point M on the larger circle to a corresponding point M’which will lie on the aerofoil. Joukowsky specified which lengths and angles to measure and explained how to use the results to arrive at the position of M’. By selecting, say, ten or twenty representative points around the circle, and following the instructions, the result is ten or twenty points that form an aerofoil shape. The more points that are transformed, the more accurately the outline of the wing emerges.
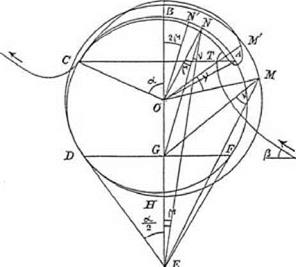
Joukowsky’s own finished diagram is reproduced here as figure 6.6. It looks complicated, but it is not difficult to identify the two main circles and the tangents, meeting at E, which were needed to start the construction. The resulting aerofoil shape can be discerned draped over the top of the diagram with its sharp tail at point C, on the left-hand side, and its rounded nose at M’on the right-hand side. The aerofoil that Joukowsky chose to construct for purposes of illustration has a marked camber and is very thick. This makes it look unrealistic, but such a degree of curvature and thickness is not intrinsic to the method. Joukowsky explained that the shape of the wing is determined by the three parameters, a, b, and a. As the circles are made larger or smaller and the point E is moved closer to, or farther from, the circles, so the shape of the wing is modified, and it can be made more rounded or more slender. In the limit, as b ^ a, and the larger circle comes ever closer to the smaller
|
|
|
FLf.. 4-
figure 6.6. Joukowsky’s geometrical construction of a winglike profile. The strongly cambered profile
|
stretches across the top of the figure, having its trailing edge near the letter C, on the left, and its leading edge near the letter M’, on the right. From Joukowsky 1910, 283. (By permission of Oldenbourg Wissen – schaftsverlag GmbH Munchen)
circle, the profile of the wing becomes so thin that it turns into an arc. In fact, it turns into Kutta’s arc.
Joukowsky then showed how to construct his second contour. He gave another set of instructions, this time involving trigonometry as well as geometry. Again the process started from two circles, one of radius a, and one of radius b, with b > a. The circles have their centers on the x-axis, and so their point of contact must also lie on the x-axis. Using the center of the smaller circle as the origin O, each point M on the larger circle can be specified by measuring the length r of the line joining O to M and the angle 0 between the line OM and the x-axis. Joukowsky gave the rules for transforming a point M into the corresponding point M’on the contour that is to be constructed. The rules gave the x – and y-coordinates of M’ in terms of the values of r and 0 that specified M. Thus,
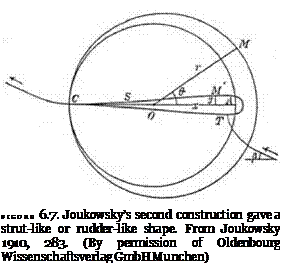 |
Figure 6.7, taken from Joukowsky’s paper, shows that the larger circle b is transformed into a streamlined, rudderlike shape lying symmetrically along the x-axis. The thickness of the rudder depends on the relative size of the circles. As b ^ a, the rudder gets thinner and eventually turns into a straight line of length 2a lying along the x-axis. The arc and the line that constitute a sort of skeleton for the thicker shapes were referred to by Joukowsky as the “bases” of his contours.
The second, empirical, installment of Joukowsky’s paper was published in 1912, two years after the theoretical part. He focused attention on two, aerodynamically important properties of his theoretical contours that could be made accessible to empirical testing. The two characteristics were (1) the angle of zero lift, that is, the small (and often negative) angle of incidence at which the wing first begins to produce lift, and (2) the slope of the graph when the coefficient of lift was plotted against the angle of incidence. Both of these angles could be deduced from the basic principles of the circulation theory. Their analysis proceeds in a similar way for all aerofoil shapes derived from a conformal transformation of a circle.52 This approach enabled Joukowsky to derive his predictions using Kutta’s lift formulas and then make experimental comparisons between models of Kutta’s arc-like wing and his own wings and rudders. The predictions applied (approximately) to all the profiles.
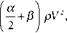 |
To address the angle of zero lift, consider again Kutta’s formula for the lift P on a circular arc at an angle в to a flow of velocity V. Kutta found that
where a is the radius of the circular arc of the wing and a is half of the angle
subtended by the arc. Assuming that the velocity V is not zero, then, if the lift is to be zero, the term sin (a/2 + P) must equal zero. In other words, P must equal – a/2. So – a/2 is the angle of zero lift, and it is determined by the geometry of the wing. When Lilienthal selected a wing based on a circular arc, and decided that it should subtend an angle of 2a at the center of the circle, he was implicitly fixing the value of the angle of zero lift. More precisely, he was fixing the angle of zero lift, provided all the assumptions of the theoretical analysis held true. It is striking that such a significant parameter should emerge so readily from the theory, and it was a consequence of the analysis that could be easily tested.
The other angle that interested Joukowsky was the slope of the lift- incidence curve. Joukowsky simplified Kutta’s formula by supposing that the arc of his wing could be treated as equivalent to two straight lines, one connecting the trailing edge to the highest point of the arc, the other connecting the leading edge to the highest point. The length of the two lines was designated /, and elementary trigonometry showed that / = 4a sin a/2. Substituting this in Kutta’s formula for the lift P gave
P = np/sm^O. + ej V2.
Joukowsky then made two further changes to the formula. First, he replaced the lift by a coefficient of lift called Ky. This was done by dividing both sides of the above equation by V2 and /. Second, for small angles, the sine of an angle equals the angle itself (measured in radians). The equation then becomes
^+e •
Joukowsky noted that the angle (a/2 + P) represented the angle of incidence as measured from the line of zero lift. If the approximations are reasonable, and if the theory was on the right lines, this formula showed that a graph of the lift coefficient against angle of incidence should have the slope np. Jou – kowsky gave the slope the label K. So here was a second testable prediction. He worked out that for a temperature of 20° and an atmospheric pressure of 760 mm, the slope of the graph should be K = 0.39.
Joukowsky had built a wind tunnel in the TH in Moscow. The tunnel had a rectangular, working section of 150 X 30 cm and could achieve wind speeds of up to 22 m/sec. The wing sections under test were suspended vertically, with their ends close to the top and bottom of the tunnel, so that they approximated an infinite wing. The sections were rigidly fastened to a framework, and the forces were measured by the weights that were needed to counterbalance them and keep the framework in equilibrium. The wing and rudder contours to be tested had been constructed so that they accorded with the outcome of the geometrical transformations described in the earlier part of the paper. The wing form had been constructed geometrically using a small circle with radius a = 750 mm and with the larger circle of radius b = 762.5 mm and an angle a = 20°. This gave a much thinner and flatter section than the heavily cambered one shown in the diagram in the first installment of the paper. The more slender of the two rudder shapes was generated from two circles a = 250 mm and b = 260 mm, whereas the fatter model was based on two circles a = 250 mm and b = 270 mm.
Joukowsky’s graphs of his experimental measurements revealed the familiar pattern when lift and drag coefficients are plotted against the angle of incidence. The lift increased in a roughly linear fashion with angle of incidence up to about в = 15°, while the drag stayed low until about the same point and then increased rapidly. Joukowsky immediately noted that his coefficients of lift and drag had higher values than those reported by Eiffel for comparable shapes. This sort of discrepancy between the wind tunnels in different national laboratories was to plague experimental work for many years. In this case Joukowsky suggested that the Moscow experiment approximated more closely the infinite wing assumed in the theoretical calculations. The important question, though, was whether his experimental graphs corroborated the theoretical predictions.
Joukowsky found that the angle of zero lift for his theoretically derived wing profile fitted more closely to the predicted value than did the Kutta – like arc that Joukowsky called its “basis” or skeleton. But even the model wings that were meant to conform to the Joukowsky profile did not achieve quite the predicted degree of lift. The wing ceased to give lift at -6°, and the circular arc that was its basis at around -4° compared with a theoretical value of (a/2) = -10°. Some of his computed values of the slope K, however, were very close to the predicted value where K = pn = 0.39. Thus he reported that K = 0.38 for the arc, K = 0.37 for the wing, but only K = 0.30 for the rudder.
The wind tunnel at the Moscow TH was soon to figure again in the pages of the Zeitschrift fur Flugtechnik. In June 1912, Joukowsky’s assistant G. S. Lou – kianoff published graphs showing the lift, drag, and center-of-pressure characteristics of the wing contours of seven types of aircraft that were currently flying with success: the Breguet, Antoinette, Wright, Bleriot, Farman, Hen – riot, and Nieuport machines.53 As von Mises observed, these early Moscow experiments gave a slope for the lift-incidence curve that closely corresponded to the theoretical value, though later experimenters found a slightly smaller value. In general, said von Mises, two-dimensional wing theory overestimates the slope by about 10 percent and underestimates the angle of zero lift by one or two degrees.54 But it was the theoretical achievement, rather than the experimental work, that proved most significant. Joukowsky’s aerofoils, the J-wings, as they were sometimes called, aroused an immediate and positive response in Germany. The interest in the theory was not abstract, aesthetic, or otherworldly. Joukowsky’s theoretical profiles became the focal point for a series of developments that brought the mathematical analysis of lift into intimate contact with both physical reality and engineering practice.