Section iv. the lift on the curved surface

Having arrived at the value of the circulation, Kutta immediately multiplied the circulation by the density of the air and the speed of flight to give the lift. He did not state the relevant formula, L = p V Г (where Г = circulation), but he used it implicitly. Here, then, was the lift on a Lilienthal-type wing specified in terms of known quantities: p, the density of the air; V, the speed of flight; r, the radius of the circular arc of the wing; b, the length of the wing; a, which was half the angle subtended by the arc; and p, the angle of incidence. The formula was

а (а і

Lift = 4npV2rbsin—sinI ~+P •

Kutta did not simply take the general lift formula p УГ for granted. He an­nounced that he was going to offer a general proof based on energy consid­erations, which he proceeded to do. The proof not only gave the magnitude of the resultant aerodynamic force as the product of density, velocity, and circulation, but it also carried the implication that the force must be at right angles to the direction assumed by the free stream at large distances from the wing.31 In other words: there was no drag. Given that Kutta was treating the air as an ideal fluid in irrotational motion, this result was a necessary conse­quence of his premises.

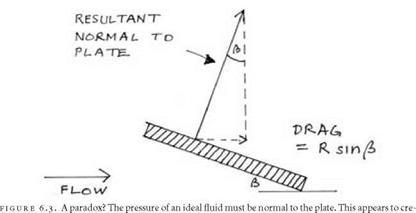
Kutta now had to confront a logical problem. If the fluid is perfect it will slide effortlessly over any material surface. This means that it can only exert a force normally to the surface. Consider a flat plate in a steady flow of ideal fluid and add a circulation around the plate. Suppose that the flow at a dis­tance from the plate is horizontal and that the plate has an angle of attack p to this flow. If the forces on the plate are normal to the plate, then won’t the resultant R be normal to it? It will be tilted back at an angle p to the verti­cal (see fig. 6.3). The resultant R will then have a drag component of R sinp. This contradicts the result of the general lift theorem, which Kutta had just proved, where the resultant is vertical, that is, normal to the flow but not

normal to the plate, so that the drag component is 0. Kutta was primarily considering an arc, not a flat plate, but the same result holds even though the geometry is more complicated. Much of the rest of his paper was spent exploring this apparent paradox.

Kutta said there was no contradiction because the force resulting from the normal pressures was not the only force at work. There must also be another force that operates on the very tip of the plate, hence his remark in the intro­duction when he said that the lift had two components. Kutta thus identified a suction force that was tangential to the surface at the leading edge. When this force is combined with the normal pressure forces, the resultant is verti­cal. The forward component of the suction counterbalances the backward component of the pressure forces to produce the zero-drag outcome. Again, the situation can be seen more simply with a flat plate. The tangential suction and the normal pressure forces on the plate are shown in figure 6.4. Intro­ducing the leading-edge suction restores consistency with the results of the kinetic energy proof that Kutta had provided for the law of lift.32

Kutta did not treat the leading-edge suction as a mere device to avoid a problem. He proceeded to investigate the flow field near the leading edge by introducing various approximations and assumptions about the shape of the streamlines. An idealized fluid flowing around an idealized, sharp edge would have an infinite speed. This would produce an infinitely large suction force concentrated on an infinitely small area, which suggests that the math­ematics would assume the indeterminate form ^/0. By reasoning that the approximate shape of the streamline would be that of a parabola, Kutta used the results he had already established to argue that the actual force would

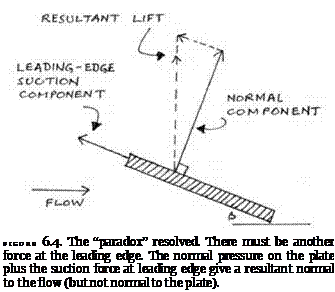converge to a determinate and finite value. He deduced that this value was exactly that which was required to turn the backward-leaning pressure resul­tant into a vertical lift and to give it the magnitude predicted by the general lift theorem.