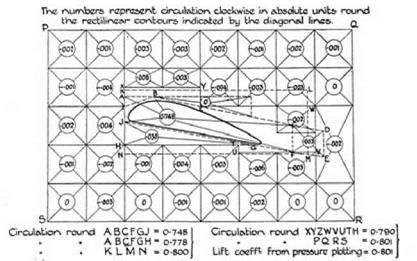
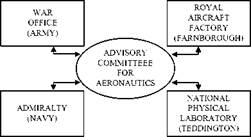
“I Was at Cambridge on Saturday”
The political pressures that originally prompted Herbert Asquith’s Liberal administration to set up the Advisory Committee for Aeronautics can be epitomized by the reaction to the first cross-channel flight from France to England, made by Louis Bleriot on July 25, 1909. Newspaper headlines declared that Britain was no longer an island. Bleriot’s heroic feat was greeted with sporting cheers, but the depressing military implications of the flight were evident. The nation’s basic line of defense had been breached. The channel was no longer a moat that made the island an impregnable fortress. Bleriot’s flight dramatically confirmed the warnings that had been voiced since the inception of “aerial navigation.” These reactions have been described in detail by the historian Alfred Gollin, who documents the atmosphere of alarm and the fear of invasion that gripped the country during the early years of the century, particularly with regard to the emerging power of Germany.7 There was anxiety, assiduously cultivated by the press, that Britain was falling behind in the race to exploit the military potential of the new flying machines: the airship and the airplane. The anxiety was expressed in newspaper reports of mysterious (and almost certainly nonexistent) Zeppelins lurking in the night skies over Ipswich and Cardiff.8
The government, represented by Richard Burdon Haldane (fig. 1.1), the secretary of state for war, did not participate in this sort of unseemly clamor. Haldane was a patrician and highly intellectual figure who combined his politics with philosophical writing and a successful legal career. Educated at the universities of Edinburgh and Gottingen, he was fluent in German, translated Schopenhauer, and had a passion for Hegel.9 To the fury of his critics the portly Haldane proceeded at his own steady pace. Much preoccupied with the long-overdue reform and rationalization of Britain’s major institutions, from the army to the universities, Haldane always insisted that a cautious and “scientific” approach was needed.10 Critics of the government policy on aeronautics called for the immediate purchase of foreign machines. Airships could be bought from France, and aircraft were on offer from the American
|
figure i. i. Richard Burdon Haldane (1856-1928). Haldane, the secretary of state for war, was responsible for the creation of the Advisory Committee for Aeronautics. He was the object of a campaign of hate and was hounded out of office. Photograph by Elliott and Fry, in Haldane 1929. |
Wright brothers, who had been the first to master powered flight. Haldane thought that Britain should go more cautiously, even if it meant going more slowly. He was disinclined to rely on the results of mere trial-and-error methods developed by others. In fact he looked down on those who proceeded in a merely empirical manner, devoid of guiding principles to broaden and deepen their understanding.11
Haldane met the Wright brothers in May 1909 when they came to Europe touting for government contracts. An editorial in Flight, on May 8, hinted at inside information and expressed confidence in the outcome of the meeting: “On Monday, Messers Wilbur and Orville Wright paid a visit to Mr. Haldane, and, while naturally it is needful and fitting to preserve secrecy as regards official matters, it may be taken as assured that our Government will duly acquire Wright aeroplanes and the famous American brothers will themselves instruct the first pupils in England.”12 In fact it was not assured. Despite much pressure and lobbying, Haldane declined to do a commercial deal with the Wrights. Rather, the minister concluded, Britain should follow the German example—or what he took to be the German example. The National Physical Laboratory at Teddington, outside London, had been founded in 1900 on the model of Helmholtz’s great, government-funded institute of physics in Berlin, the Physikalisch-Technische Reichsanstalt, and this was the pattern that Haldane wanted to see developed.13 The government must locate the best scientists that were available and set them to work on the fundamental problems of flight. The pioneers had got their machines into the air, but how and why they flew remained obscure. The working of a wing, for example, the secret of its lift, remained an unsolved problem, as did the basis of stability and control. Furthermore, it was unclear whether the future lay with heavier – than-air flight or airships. Like many others, Haldane was more impressed by airships, but scientists must address these issues in all their generality and then, with scientific theory leading practice, the best technology would be able to progress on sound principles. As Haldane put it, “the newspapers and the contractors keep clamouring for action first and thought afterwards, whereas the energy which is directed by reflection is the energy which really gives the most rapid and stable results.”14 The issue of the Wright brothers and their rebuff deserves comment. To Haldane’s critics the refusal to buy these aircraft seemed a gross error of judgment on the government’s part. In fact it was grounded in a defensible line of reasoning. The Wright machine was known to be clumsy and unstable. It could only take off along specially constructed rails, and the subsequent flight demanded great skill and ceaseless intervention by the pilot. As a British test pilot put it a few years later, in a report to the ACA on the flying qualities of different machines, it needed an “equilibrist of the first order” to keep the Wright machine in the air.15 (This judgment is corroborated by modern aerodynamic research conducted on the Wright machine.)16 The pilots of such aircraft would (1) require extensive training, (2) become exhausted on long flights, and (3) be so preoccupied that they could hardly perform any military task such as map reading, reconnaissance, or photography. The need was for aircraft that were easy to fly and would leave their pilots with spare mental and physical capacity. The British government’s view was that power in the air would go to the nation that possessed stable aircraft.17
Even before he met the Wrights, Haldane had sanctioned secret tests to be carried out at Blair Atholl, in the Scottish highlands, on a machine designed by a British inventor, J. W. Dunne.18 Dunne was a friend of H. G. Wells and later in life became well known for his metaphysical speculations on the nature of time.19 After his early military career had been terminated by ill health, Dunne turned to aviation and won the confidence of the superintendent of the Army Balloon Factory at Farnborough. Dunne’s airplane, unlike the Wrights’, was meant to be stable and, to achieve this he used a novel, swept-wing configuration. The tests, however, which took place in the summer of 1907 and 1908, were a failure, and the machine did not maintain sustained flight.20 A retrospective report of the episode in the journal Aeronautics contained the fanciful claim that, after an indiscrete mention of the trials in the press, the Scottish estate where they took place was alive with foreigners who, it was implied, must have been German secret agents. “In two days the place was buzzing with Teutons.” Fortunately, the article continued, loyal local citizenry misdirected the unwanted foreign visitors so that the nation’s secrets remained secure.21 Flight even hinted that some of these alleged spies had been disposed of by the Scotch gillies, who acted as lookouts for the trials.22 Haldane’s worst suspicions about empirics and inventors, and everything to do with them, were confirmed by such goings on.23 Dunne and his supporters were dismissed. It was time to bring in the scientists and develop a serious policy. Haldane had no intention of being deflected from this course just because the Wrights turned up in London.
Haldane had already laid out his ideas of a sound policy at the first meeting of a new subcommittee of the powerful Committee of Imperial Defence on December 1, 1908.24 The prime minister had formed the subcommittee to report on three questions: (1) the military problem that aerial navigation posed to the country, (2) the naval and military advantages of airships and airplanes, and (3) the amount of money that should be spent and where that money should go. The chairman, Lord Esher, invited Haldane to open the proceedings. Haldane said it was important to have the navy and the army working together on these issues in order to provide the preconditions for real progress. Haldane meant by this the preconditions for developing a genuine, scientific understanding of aerial navigation and the problems it posed. He went on: “I was at Cambridge on Saturday, and I spent Sunday talking over some of these questions with Sir George Darwin, the mathematician. Some of them there have given a good deal of attention to this matter, and what strikes them—certainly what has struck me—is the little attempt which has been made, at any rate as far as the War Office is concerned, to answer these questions.” Nobody in the navy, he said, would think of building ships without testing models in water, but if there was ever a need for model work it was in aeronautics. Darwin had told him that the French had experimental establishments using artificial currents of air. In reply to a direct question, Darwin had also told him that there was a great deal of mathematical work that needed to be done. Haldane therefore asked the subcommittee to consider appointing a further committee of experts to advise them on technical questions. The advisory body might have “somebody presiding over it like Lord Rayleigh or Lord Justice Fletcher Moulton, or Sir George Darwin.” This, concluded Haldane, was “a very important preliminary to any real progress.”
Esher’s committee went on to take evidence from a number of expert witnesses, such as the aviator the Hon. C. S. Rolls and, to appease Churchill, the bombastic businessman, arms dealer, and aviation enthusiast Hiram Maxim.25 The Esher committee did not succeed in bringing the interests of the army and navy into alignment and became bogged down in complicated differences over policy. Overall, it backed airships over airplanes and even recommended stopping research on heavier-than-air machines, although later this policy was quietly dropped.26 In the course of the protracted discussions, Haldane was challenged by the navy representative over the desirability of his proposed committee of scientists. Should not scientists be on tap rather than on top? Eventually Haldane got his way but, perhaps as a result of this challenge, made sure that his projected advisory committee of experts would report directly to the prime minister.