The Empirical Study of Rayleigh Flow
Reports and Memoranda No. 16, of September 1909, was a note prepared by Mallock on experiments that involved moving flat and curved plates through a tank of water and measuring the forces on them.24 The plates were rectangles whose sides were in the ratios of 2:1, 1:1, and 1:2 and were inclined at various angles between 0° and 90° to the direction of motion. Measurements were taken at various speeds between 150 and 500 feet per minute. The plates were attached to scales in order to read off the forces exerted on them. The resultant force on the plate was broken down into a resistance force (the drag directly opposing the motion) and a lateral force at right angles to the direction of travel (a lift force). A graph of the results showed that the measurements “differ greatly from the values calculated on the assumption that the pressure on the rear surface is uniform and equal to that of the fluid at a distance” (40), that is, calculated on the assumption that there was “dead water” behind the plate. Mallock’s explanation for the disparity was the same as Rayleigh’s.25 There can, said Mallock, “be no doubt that the distribution of the pressure over the rear surface and its difference from the pressure prevailing in the fluid at a distance, account both for the peculiarities of the resistance and the lateral thrust curves” (40).
There was a negative pressure at the back of the plate, and Mallock suggested that the cause of this suction effect was eddy formation: “The fact of negative pressure being found on the down-stream side of the surface is ultimately connected with the formation of eddies. . . nor will a satisfactory explanation of such features. . . be obtained until the formation of eddies under varying conditions has been investigated” (40). These ideas had already found expression in one of the very first Reports and Memoranda, that of May 19, 1909, titled “Memorandum on General Questions to Be Studied.” Much of this publication was devoted to the results of several series of experiments Mallock had performed on plates in currents of air.26 He described the general form of the curves relating angle of incidence to lift and drag. The lift increases in a roughly linear fashion but only up to a certain, critical angle. After this it declines more or less sharply. In the region of the critical angle, he noted, the airflow had an unsteady, oscillating character accompanied by the formation of eddies.
Mallock went on to make the following significant remark about the difference between perfect fluids and real fluids: “The details of eddy formation are also important. The eddy in a real fluid differs greatly from the ideal vortex ring. The latter is a separate entity which could not be made, and, if existing, could not be destroyed. The eddies in real fluids are composite structures in which layers of originally different velocities are wound up together” (22). Mallock was arguing that the turbulence that characterizes real flows cannot be modeled by the kind of vortices that can exist in a perfect fluid. He was implicitly citing one of the most important results of classical hydrodynamics. Kelvin had provided a rigorous proof of a result that had long been known in one form or another, namely, that vortex or rotational motion in an ideal fluid can be neither created nor destroyed. The governing equations of ideal flow did not allow a vortex to be generated (for example, by the motion of a solid body immersed within the fluid), nor could any existing vortex be damped down or dissipated. Mallock concluded that an adequate understanding of the flow of a real fluid (such as air), around a real object (such as a wing), cannot be achieved using a theory of an ideal, perfectly inviscid, fluid. Like Rayleigh, he now believed it was necessary to take account of viscosity.
A further criticism of Kirchhoff-Rayleigh flow was contained in Reports and Memoranda No. 24, dated April 21, 1910. This was written by T. E. Stanton, the head of the Engineering Department at the NPL, and his assistant Leonard Bairstow.27 The aim of the research was to discover the relative efficiency of the various rudders and lifting surfaces that were used on airships. Could these be modeled as flat planes set at an angle to the flow, and could Rayleigh’s formula be used to predict the forces on them? Recall that Rayleigh had deduced the formula for the distance of the center of pressure of the resultant aerodynamic force from the leading edge of the plate. Stanton and Bairstow carried out measurements in the air channel to test this. They found that “the experimentally determined position of the centre of pressure for the pattern of rudders used are in all cases ahead of the theoretical position for a thin plate” (75). Here was a second blow to the utility of Kirchhoff-Rayleigh flow. First it underestimated the force on wing; now it emerged that it located that force in the wrong place.
The next step was to try to render the flow around wings and plates visible and to capture them in photographs. The photographs were provided for the Advisory Committee in 1912 by C. G. Eden in Reports and Memoranda No. 58.28 Eden injected a mixture of aniline and toluene into the flow of water in a small water channel, a 3 X 4-inch cross section, containing a small, 1-inchwide model wing that could be given various angles of incidence. The flow had a speed of 1 inch per second and could be illuminated by means of an arc lamp. The specific gravity of the injected fluid was adjusted to match that of the water so that it did not alter the character of the flow. The optical properties of the oil were such that at an angle of about 70° to the incident beam, the oil drops appeared as bright dots and could be photographed. Commenting on the resulting photographs, Eden described the effect of putting the wing at different angles of incidence, saying, “At small angles up to 9° no eddies are formed, but it will be seen that between 9° and 10° a change takes place, and at 10° there is a small ‘dead water’ region at the back of the plate and the eddying of the flow in the wake is clearly shown” (99). At first it may seem that the photographs were evidence in favor of Kirchhoff-Rayleigh flow. Eden detected eddies that the theory could not explain, but he reported a clearly visible region of “dead water,” which is the most characteristic feature of the flow. The real significance of the photographs, however, came out when they were related to model wings as they were being studied in the wind channel.
Bairstow and Melvill Jones produced two papers in 1912 that had a direct bearing on the meaning of the photographs. The first, Reports and Memoranda No. 53, was a general assessment of the properties of aerofoils, “as deduced from the results of various aeronautical laboratories.”29 These in-
|
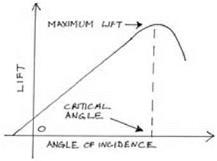
figure 3.6. The typical relation between the lift and the angle of incidence of a wing. The lift increases in a linear way with increased angle of incidence up to a critical angle, at which the lift begins to decline rapidly. At this angle the wing “stalls.” Notice that a typical wing still generates some lift for small negative angles of incidence, that is, when sloping down. |
cluded Eiffel’s near Paris and Prandtl’s in Gottingen. These results, said Bair – stow and Jones, made it possible to identify the salient features of aircraft wings, both qualitatively and quantitatively. Suppose a wing is aligned with the general direction of airflow. It generates a lift force at right angles to the direction of flow, and as the angle of incidence is slowly increased the lift increases in an approximately linear manner. At a certain point, around 10° to 15°, the lift reaches a maximum and then declines, sometimes very sharply. This was Mallock’s “critical” angle. Finally, because the wing produces lift when it is horizontal, the position of zero lift must occur when the wing has a slight negative angle of incidence. The general form of the graph relating lift to incidence, as described by Bairstow and Melvill Jones, is indicated in figure 3.6.
In their next report, “Experiments on Models of Aeroplane Wings,” of March 1912, Bairstow and Melvill Jones made two important moves.30 First, they reinforced the evidence that the factors regulating the amount of lift in a wing are precisely those that are excluded by the discontinuity theory, namely, the shape of the upper surface. Second, they made the crucial link to Eden’s photographs. To show the significance of the upper surface, they used a series of aerofoil sections with a flat base but (1) varied the camber of the upper surface and then (2) altered the position along the chord of the maximum ordinate. (The camber was measured by the ratio of the maximum height of the curved upper surface to the chord.) They demonstrated how changes in camber altered the ratio of the lift to the drag. Thus, starting from a nearly flat wing, an increase in camber at first increased and then decreased this ratio, the maximum being for a wing with a curvature of 0.05. The optimum position of the highest point in the upper surface turned out to be one-third of the chord from the leading edge. Variation of the curvature of the lower surface of the wing, by contrast, produced little effect on the lift or drag. Thus the systematic accumulation of inductive evidence about the behavior of wings consolidated Rayleigh’s early doubts about his classic results. The most significant aerodynamic processes on a wing had, on his analysis, been located on the wrong surface.
Eden’s photographs showed a winglike shape at various angles below and above the critical angle. At small angles there were no eddies, so the flow was smooth and stayed close to the surface of the plate or wing. Around 9°, eddies formed behind the plate and the smooth flow broke down. Here the illuminated oil drops stayed as spots of light and did not show up as lines because they did not move during the exposure time. As Bairstow and Melvill Jones put it, “It seems clear that the alterations in pressure at the critical angle are due to the sudden breakdown in the character of the fluid flow in the neighbourhood of this angle, and in this connection the photographs . . . are of interest. . . . It will be noted that above the critical angle the fluid near the upper surface is practically ‘dead’” (10).
The implication was that dead air does indeed form behind a wing, as in Rayleigh flow—but only after the wing has passed the critical angle. Bairstow, Melvill Jones, and Eden were all aware that this reasoning had a weakness. The experiment was in water while the conclusion was about air. The conditions of similarity, required for a confident inference from the one phenomenon to the other, were not strictly satisfied.31 The fact remained that the photographs that looked most like Kirchhoff-Rayleigh flow showed a wing that was over the critical angle.32 This information pointed to an important but disconcerting conclusion. The mathematical studies devoted to Kirchhoff-Rayleigh flow were not describing at all how a wing can be so effective in producing lift. In as far as this model of flow over a wing approximated to reality, it was actually describing the breakdown of the pattern that was required for the efficient working of a wing. If they described anything, the formulas of Kirchhoff – Rayleigh flow were the mathematics of a stall, when lift fails. They described the situation when an aircraft was about to fall out of the sky.33