The Equation of Continuity (and Some Conventions)

The equations of motion for an ideal fluid were derived from two basic state­ments. In a sense, said Cowley and Levy, “these two statements and all that they involve are a definition of the nature of the fluid.” Furthermore, “all de­ductions regarding its behavior can only be a recasting of these [statements] into a new but equivalent form” (37). The two statements were as follows:

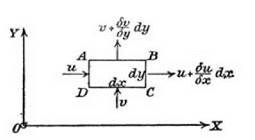
(1) The mass of fluid in any region remains constant. This is called the condi­tion of “continuity.” And (2) the motion of every fluid element is consistent with Newton’s Laws of Motion. To spell out the first of these principles, con­sider a small volume through which the fluid flows. This is represented in cross section in figure 2.1 by the rectangle ABCD, with sides labeled dx and dy. Before going further I should say something about the conventions used in such diagrams in hydrodynamics. The d and 8 (delta) symbols indicate that the lengths are not just “small” in a commonsense manner of speaking but have been, or will be, made “infinitely small” in the course of the mathemati­cal reasoning. They will be subject to a “limiting process” in which it is as­sumed that they can be made ever smaller without the shrinkage demand­ing any significant changes in the pattern of reasoning (which is essentially what Lamb meant in the passage quoted at the head of the chapter). The reason why the volume can be represented by an area is because the volume is assumed to be of unit depth, so the number 1, representing the depth, is present but can be suppressed. Diagrams of this kind thus amount to a two­dimensional cross section of the flow, and the situation portrayed is routinely referred to as a two-dimensional flow.14

Two-dimensional flow diagrams do not allow any representation of what happens at the edges of the figure other than those shown in the cross section. The parts of the object that go into, and out of, the page are not shown. In describing a situation in this truncated way, the mathematician assumes that nothing significant happens at the edges that are not represented. In reality this is not true, so all discussions of two-dimensional flow are by their na­ture simplifications. These simplifications will become especially significant when the object under discussion is a wing and the cross section takes on the shape of an aerofoil. In the literature on aerodynamics the simplified, two-dimensional diagram of the flow is then often called a diagram of the flow around an “infinite” wing. This usage can be disconcerting, but it is simply a way of saying that the flow shown in the picture is representative of what goes on in the central parts of the wing. The wingtips are assumed to be

sufficiently far from the action that they do not interfere in any way and can be ignored. The literature on hydrodynamics and aerodynamics is full of ref­erences to infinity. The word “infinity” can nearly always be read as meaning either “so far away that it causes no disturbance” or “so far away that it can be considered to be undisturbed.”

Having dealt with these terminological matters, I now come back to the small volume represented in figure 2.1.15 The fluid is assumed to be incom­pressible with constant density p, so in a given time interval the mass of fluid flowing into the volume always equals the mass flowing out. In the x-direction the speed of flow into the volume is designated by u and the speed of outflow by ^u+d~^x j. The symbol du/dx means “the rate of change of u with x,” so the expression in parentheses refers to the original speed plus the change of speed. The change can be positive or negative. The mass entering the control volume per unit time is puby and the mass leaving is pi u+—Sx | Sy. The

I dx j

same procedure is repeated for the flow in the y-direction. In each case the quantity of fluid entering and leaving the control volume is obtained by mul­tiplying the speeds by the density of the fluid and dimensions of the face crossed by the flow. Mathematically, the condition of continuity is then ex­pressed by summing all these quantities and equating the sum to zero. Fluid in must equal fluid out, with zero shortfall. When the expression for this zero sum is simplified, the equation that results takes the form

du + dv 0 dx dy

This expression states, in a mathematical form, the condition of continuity.