The law of Biot and Savart received a number of further aerodynamic applications before the outbreak of World War I. All of these were published in the Zeitschrift fur Flugtechnik and came from the Gottingen group. Four of them were by Albert Betz and one by Carl Wieselsberger. I describe them briefly, keeping to the chronological order of their appearance.
In September 1912 Betz published some wind-channel results that showed that a wing operating in the vicinity of the ground would experience an increase in lift.61 Betz showed this by testing a model wing in a channel fitted with a false floor that could be raised or lowered. The phenomenon was an important one. Aircraft necessarily fly near the ground on landing and takeoff. Pilots were aware that there was a change in flying characteristics produced by these circumstances, but the nature of the change was little understood. This “ground effect” explains why an overloaded aircraft can sometimes take off with apparent success and then fail to gain height, with disastrous consequences. It also explains why some early aircraft could “fly” but never got more than a few feet above the ground.62 Betz also wanted to get a quantitative estimate of the effect of the walls of a wind channel on the measurements that were carried out in the course of experimentation. He showed that Prandtl’s new theory could lead to rough but quantitative predictions that were confirmed by experiment. (The results were approximate, Betz suggested [220], because the “horseshoe” model ignored the downward motion of the trailing vortices.) Both of the subjects that Betz broached in his brief paper were to become a matter of enduring concern and research in subsequent years.
In January 1913, Betz published a second study, this time of the lift and resistance of a biplane.63 Whereas Foppl had used the Biot-Savart law to study the effect of the induced velocity on the tail wing, Betz now used the same approach to study the mutual interaction of wings that were positioned one above the other. The central point about the application of Prandtl’s approach to a biplane is that the trailing vortices from the upper wing will generate an induced resistance not only in the upper wing itself but also in the lower wing, while the trailing vortices from the lower wing will likewise affect both wings. Furthermore, if the wings are not located directly one above the other, the bound vortex corresponding to the wing itself (and not just the trailing vortices) will have to be taken into account when computing the induced velocity and induced drag on the other wing.
With the exception of Kutta’s second, 1911 paper, this work represented the first serious engagement with the theoretical aerodynamics of the biplane and the difficult problem of the mutual interaction of the different parts of an aircraft. It will be recalled that the “practical men” in Britain stressed holistic effects to justify their conviction that only the intuition of the engineer could cope with the problems of airplane design. Scientists and mathematicians, they said, simplified problems by studying one part at a time, which doomed them to failure. Such a procedure ignored the all-important effects of interaction. Perhaps (had they known about it) the “practical men” would have been impressed to be told of the progress that was being made in Gottingen. Here engineers, such as Betz, were using the Biot-Savart law to put the study of interaction on a mathematical as well as an experimental basis.
Betz carried out wind-channel measurements of the lift and resistance of a set of two wings rigidly fastened into a biplane configuration. He studied (a) the effect of varying the distance apart of the wings, (b) the effect of giving the wings different angles of incidence from one another (decalage), and (c) the effect of placing one wing ahead of the other (stagger). He found that the effects were small within the range he studied, though the most significant variable was the stagger of the wings. One of his practical concerns was to form some idea of the relative merits of monoplanes and biplanes. He summed up his results in four propositions: (1) A biplane arrangement with wings of equal span always has a less favorable ratio of lift to resistance than one of the wings taken separately. (2) A biplane can have advantages over a monoplane when the rest of the resistance of the aircraft, for example, a bulky fuselage, is taken into account. (3) A biplane is at an advantage if a high lift at low speeds is required. (4) The greatest maximum lift is obtained when
the upper wing of a biplane is placed ahead of the lower wing and is given a slightly smaller angle of incidence than the lower wing. All of these results, said Betz, were rendered intelligible by Prandtl’s theory, and the empirical graphs of lift and resistance were duly accompanied by theoretical curves calculated from the theory.64
In neither of his papers did Betz specifically mention, or illustrate the use of, the Biot-Savart law. He alluded to the horseshoe model but revealed none of the mathematics involved in his calculations. Like Foppl he promised the reader that a fuller account was to follow from the pen of Prandtl himself. The Great War began in July 1914, but there seemed no immediate concern with secrecy. In a paper that appeared in August 1914, Wieselsberger preempted Prandtl and stated the Biot-Savart law explicitly and illustrated its application.65 He asked why birds often fly in a V formation. He did not manage to answer the question, but he did succeed in laying out the basic ideas, and the basic mathematics, of Prandtl’s theory. In approaching the problem of formation flying, Wieselsberger ignored the beating wing motion involved in bird flight and treated birds as small airplanes. He then followed Prandtl and treated the airplane as a horseshoe vortex. By the use of the Biot-Savart law he showed that on either side of the horseshoe vortex there would be an updraft. This, he argued, allowed another wing, positioned to one side of the first wing, to operate at a more favorable angle of attack. This lowered the component of induced resistance in the direction of flight. On the basis of some plausible numerical assumptions, he made a quantitative estimate of the advantages to be derived from flying in the updraft of neighboring birds. His overall model, however, led to the conclusion that side-by-side flight would be just as efficient as the V formation.
In September 1914 Betz produced a study of wings with a sweepback and a twist at their ends,66 a configuration frequently used by designers of German aircraft at that time. The name Taube, or “dove,” was given to such machines. In Betz’s paper there was a passing reference to yet another formula attributed to Prandtl and his new theory, though again no derivation was given. The formula concerned the minimum glide-angle that could be expected for a wing of given span and lift. The main result of Betz’s experiments on a range of Taube-style wings was to confirm the near optimum character of very simple, rectangular wings. Having neither twist nor sweepback, such wings also had an economic and practical advantage: they were easy to construct. The glide coefficient (given by the ratio of resistance over lift) was not significantly improved by sweepback or twist, though Betz did find they improved longitudinal stability.
Perhaps because the promised theoretical paper from Prandtl was not forthcoming, Betz finally published his own account of the mathematics underlying his papers. Titled “Die gegenseitige Beeinflussung zweier Trag – flachen” (The mutual influence of two wings),67 the work appeared in the Zeitschrift fur Flugtechnik for October 1914. Betz concentrated on the case of the staggered biplane with wings of equal span where the upper wing was positioned ahead of the lower wing. Because the analysis proceeded on the assumption that each wing and vortex system could be represented by the simple “horseshoe” schema, the only real novelty in the paper lay in the more complex geometry of the computations, but the explicit development of the mathematics of the theory demonstrated its applicability to what was then a vitally important form of aircraft. It was clear that Prandtl and his colleagues now had a theory that could be used to predict the induced resistance of biplanes, or triplanes, using only the wind-channel data for a single wing.
‘In the same year, 1914, Wieselsberger also published a survey article that described the state of knowledge in German aerodynamics with respect to lift and drag. It did not appear in the ZFM but in an Austrian journal, the Osterreichische Flug-zeitschrift.68 The article covered both two-dimensional and three-dimensional theory and took the reader through the work of Kutta, Joukowsky, Deimler, and Blumenthal and up to Prandtl’s horseshoe vortex. Wieselsberger’s survey effectively brought up to date an earlier survey by Reissner, of the TH in Aachen, which had laid stress on questions of stability and propeller theory.69
The international situation had been deteriorating throughout 1914, and British statesmen, such as Lord Haldane, became increasingly worried about the “war party” surrounding the German kaiser.70 With the threat of war, it was ever more important for European countries to monitor the technology of their potential enemies. If anyone had wanted to keep an eye on German aviation, the papers of Foppl, Betz, and Wieselsberger would have given them all they needed to know about the general state of scientific knowledge in the field of aerodynamics. These publications would have made clear that the circulation theory of lift was wholly taken for granted in Gottingen and the German-speaking world. Collectively, the publications showed that the theory had been developed to the point where it was being applied to problems of practical importance. Betz’s theoretical analysis of the biplane, however, was the last of the Gottingen research papers to appear in an open and accessible format. Thereafter they would be hidden away from public view in the Technische Berichte, published in individually numbered copies by the military authorities and marked Geheim—“secret.” In the meantime, the Gottingen results were in the public realm and were available to anyone in Cambridge or London who cared to study them.
Making the Horseshoe Model More Realistic
Prandtl never produced the promised article in the Zeitschrift fur Flugtech – nik. This was not because he harbored reservations about the approach. On the contrary, he was happy to produce accounts for general surveys, for example, in volume 4 of the Handworterbuch der Naturwissenschaften published in 1913. The handbook was an encyclopedic survey of the state of the natural sciences and contained articles by both Fuhrmann and Prandtl. Fuhrmann wrote on hydrostatics, and Prandtl wrote on fluid dynamics.71 In his contribution Prandtl gave an explicit account of the circulation theory and presented a graph contrasting Kutta flow with Kirchhoff-Rayleigh flow (136). He also cited Lanchester’s work and gave a diagram (112) that laid out the qualitative basis of the horseshoe model, though the Biot-Savart law was not mentioned by name. Why the hesitation? The simple horseshoe model was clearly in a provisional state and was still undergoing revision. It contained formal features that compromised both its empirical adequacy and its practical utility. Despite the successes of the theory, it would have been understandable if Prandtl had wanted to remove these limitations before presenting the approach to a specialist readership. The time was hardly ripe for an authoritative presentation, which may explain the non-appearance of the article. Then the war intervened, and the form and level of presentation at which he seems to have been aiming were not achieved until 1918.
The problems with the “horseshoe” vortex were both mathematical and physical and were closely interconnected. Mathematically there was the difficulty arising from the singularity in the Biot-Savart formula which has already been remarked on, that is, the problem that arises when h = 0. The formula implied that the velocity of the downwash at the wingtips became infinite. The formula yields this result because of the uniformity of the vortex distribution implied by the model, that is, the constant value of the circulation along the bound vortex and hence along the span of the wing. This was a physically false picture. The existence of lift implies that there must be a greater pressure beneath the wing than above it, but the finite length of a real wing allows the air at high pressure beneath the wing to move round the tip to occupy the lower-pressure region above the wing. Such freedom of movement ensures that the pressure difference between the upper and lower surface will be zero at the tips. There will therefore be no lift at the tips and hence no circulation. Circulation cannot be constant along the span in the way that was assumed in the simple horseshoe model; it must fade away to zero at the tips.
Prandtl’s problem was to find a model with a more realistic lift distribution along the span of the wing. His response was ingenious. He complicated the simple horseshoe model by introducing a number of horseshoe vortices laid out in the fashion indicated in figure 7.11. (A similar figure was used in an early article by Betz.)72 Starting from a single “horseshoe” whose span coincided with the full span of the wing, he added others of smaller span. The parts of the vortex that lie along the span are to be thought of as piled on top of one another. In this way the constant distribution of circulation along the span is replaced by a variable, stepwise distribution with a maximum at the midpoint. The arrangement had the consequence that vortices now trailed from a number of points along the rear edge of the wing, rather than merely at the wingtips. This stepwise model, however, was only the starting point of Prandtl’s line of reasoning.
Prandtl did not simply introduce a number of horseshoe vortices such as the five in the diagram, or even 50 or 500. He introduced an infinite number. He postulated an infinite number of vortices of infinitesimal strength. The vortices were infinitesimal for two reasons. First, an infinite number of vortices of finite strength would result in the absurdity of a wing with infinite circulation and infinite lift. Second, he needed the circulation and the lift at the tips to approach zero. A stepwise model with finite vortices would merely reproduce the problem that dogged the original. The vortices had to become infinitely small at the wingtips. Along the span of the wing the infinitesimal vortices were assumed to be compressed into a single line of bound vortic – ity (of varying strength) called the lifting line. These refinements made it possible to imagine a smooth, rather than stepwise, lift distribution that was amenable to mathematical treatment. To accord with the known facts, the
|
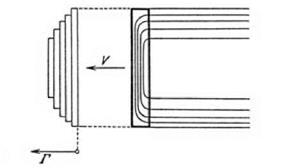
figure 7.11. Stepwise complication of the simple horseshoe model. Prandtl made the horseshoe model more realistic by multiplying the number of horseshoe vortices and imagining them stacked on top of one
another. From Tietjens 1931, 209. (By permission of Springer Science and Business Media)
|
smooth lift distribution had to have a maximum lift at the midpoint of the span and approach zero lift at the wingtips.
Having described Prandtl’s refined model in qualitative terms, I now show how he expressed these ideas in mathematical terms. This account will prepare the ground for the next two sections, which describe the technical and mathematical heart of the Gottingen achievement.
Suppose the wing has a span b and lies along the x-axis of a coordinate system so that it runs from x = —b/2 to x = +b/2. The distribution of the circulation can then be represented by Г(х). The symbol indicates that, for every value of x along the axis between the wingtips, there corresponds a specific value of Г, the circulation. Thus Г(о) is the value at x = 0, the origin, which, following convention, is taken as the center of the wingspan. It is known from experiment that the lift is at its maximum value at this central position. Because it plays an important role, it is customary to give the circulation at this point a special designation and write Г(о) = Г0. The lift and hence the circulation is zero at the tips, so that Г(—b/2) = 0 and Г(+Ь/2) = о. For the moment, and for the purpose of conveying the main outlines of Prandtl’s theory, the actual shape of the lift distribution need not be given in more detail than this. The mathematical shape described by the function Г(х) will, for the moment, remain unspecified, but it will be some smoothed-out version of the shape made by the stepwise lift distribution. The details are reserved for the next section. For the remainder of this section, the distribution is simply referred to as Г(х) so that the general structure of the mathematical reasoning can be rehearsed. My aim is to show, in general terms, how Prandtl used the Biot-Savart law to calculate the lift, the induced velocity, and the induced drag.
The first step was to relate each of the infinitesimal horseshoe vortices to the Biot-Savart law. The relevant version of the formula for a vortex of finite strength has already been stated, namely, w = —r/(4nh). Because the analysis was now to be applied to infinitesimal vortices, the formula became dw = —dr/(4nh). The goal was to calculate the downwash at some specified point on the wing with the coordinate, say, x = x’. All of the infinite number of trailing vortices (each coming away from the wing at some point with its own specific x-coordinate) will contribute to the downwash at the point x’. The Biot-Savart law gave the (infinitesimal) contribution dw made by each of these infinitesimal vortices. The perpendicular distance h in the formula needed to be re-expressed as (x’ — x). This was the distance between the point on the wing from which the infinitesimal vortex emerges and the point x’ at which the downwash was to be found. A process of integration that adds the contribution of all the infinitesimal trailing vortices would then give the total
downwash at X. A further calculation, and a further integration, was needed to get the downwash for the entire wing, that is, for all the points like x’ which lie along the span between x = – b/2 and x = +b/2.
The procedure that has just been sketched was based on the assumption that the quantity dr used in the Biot-Savart formula corresponded to the strength of the infinitesimal vortex at the arbitrary point x. How was this infinitesimal strength to be expressed? The answer was that the strength of the element of trailing vorticity issuing from a point x was equal to the change of vorticity on the wing at that point. This can be explained by going back to the stepwise model of a finite number of finite vortices that was shown in figure 7.11. First the outer horseshoe is put in place. Suppose this has strength Tj. Then the second horseshoe is added, which has strength Г2 and a slightly shorter span, then Г3 is added, which again has a slightly shorter span, and so on. Consider the two points on either side of the origin of the x-axis from which the trailing vortices of strength Г2 emerge. These are the points at which the distribution of circulation changes by an increase of the amount Г2. Thus the strength of vorticity trailing from the wing at that point equals the change in vorticity around the wing at that point.
This “strength equals change” rule holds even when there are an infinite number of infinitesimal horseshoe vortices. The distribution of circulation along the span is given by the curve r(x), so the change in circulation is the slope of the graph of r(x) multiplied by the distance over which the slope reaches. The slope is дГ/dx, and the distance is dx, so the change whose value is sought is dr = (дГ/dx) dx. This expression gave the strength of the circulation or vorticity to be entered into the formula for the Biot-Savart law. The infinitesimal contribution of the vorticity at x to the downwash at x’ was therefore
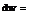 (ЭГ / dx ^jdx 4n(x’ — x)
(ЭГ / dx ^jdx 4n(x’ — x)
The total downwash at the point x’, designated by w(x’), is the integral of all of these infinitesimal contributions, summed over all the vortices issuing from the whole span of the wing. Thus,
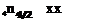 /X 1 +if2(dr / dx )dx w(x ) = -— I Л-Ж J
/X 1 +if2(dr / dx )dx w(x ) = -— I Л-Ж J
The above integral has a singularity at x = x’, when the denominator becomes zero, but the integration could be carried out in such a way as to avoid this problematic point.
Given the downwash it was then possible to calculate the induced angle of incidence at X. This angle, ф, follows from the value for w(x’) because it was simply the angle made by combining the downward induced velocity with the free-stream velocity. The ratio of the two speeds gave the tangent of the angle ф, but because the angle was small, the angle and tangent could be equated. The induced angle of incidence was
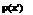 w(x’) V ‘
w(x’) V ‘
The lift distribution could now be related to the overall lift and induced drag. Recall that for an infinite wing the flow at every cross section resembles that at every other cross section. The lift per unit length is constant and is given by the Kutta-Joukowsky formula as L = рГV. Prandtl took this formula to apply to each separate, infinitesimal element of a three-dimensional wing, with the proviso that the circulation would vary from element to element according to the distribution Г(х). The overall lift could then be represented by the integral of all the elementary lifts: dL(x) = р V r(x)dx. Thus,
+b/2
Lift = pV J Г(х)dx.
—b/2
Each point on the wing would generate an element of downward velocity and would thus be subject to a slight downward slope in the local flow. The element of lift dL(x) at that point would be tilted backward (relative to the main flow) so that the resultant force possesses a component opposing the motion. This was the induced drag. The induced drag at a given point x depended on the induced angle of incidence ф at that point. The component of induced drag resulting from the backward tilt equals dL(x) sinф(x). For small angles the sine of ф is equal to ф itself, so the element of induced drag was dL(x) ф^). Thus the total induced drag was given by the integral
+ b/2
Drag = pV J Г(х)p(x)dx.
— b/2
This relation could be expressed in terms of a coefficient of induced drag by dividing the value of the drag force itself by Уг р V2F, where F is the area of the wing. This gave the coefficient of induced drag as
2 +b/2
CD = — J T(x)<p(x)dx.
—b/2
It will be evident from these formulas that a closely knit structure of theoretical relations was emerging in Gottingen which connected lift, drag, span, and the distribution of circulation along the span of a wing. For the purposes of exposition I have only presented this structure in a schematic form. The mathematical formulas just given all depend on the distribution of the circulation, Г(х), but the actual character of the function governing the distribution has remained unspecified. All that the above formulas entail is that if the distribution Г(х) is given, then the lift, the induced angle of incidence, and the induced drag can be calculated. Only when the distribution is specified will the theory will have real content. The next question is: How was the distribution of lift and circulation found? How is Г(х) to be defined?
![]() Z+1
Z+1











