Aerodynamics

In March 1984, with the Copper Canyon studies showing promise, a classified program review was held near San Diego. In the words of George Baum, a close
associate of Robert Williams, “We had to put together all the technology pieces to make it credible to the DARPA management, to get them to come out to a meeting in La Jolla and be willing to sit down for three full days. It wasn’t hard to get people out to the West Coast in March; the problem was to get them off the beach.”

One of the attendees, Robert Whitehead of the Office of Naval Research, gave a talk on CFD. Was the mathematics ready; were computers at hand? Williams recalls that “he explained, in about 15 minutes, the equations of fluid mechanics, in a memorable way. With a few simple slides, he could describe their nature in almost an offhand manner, laying out these equations so the computer could solve them, then showing that the computer technology was also there. We realized that we could compute our way to Mach 25, with high confidence. That was a high point of the presentations.”1

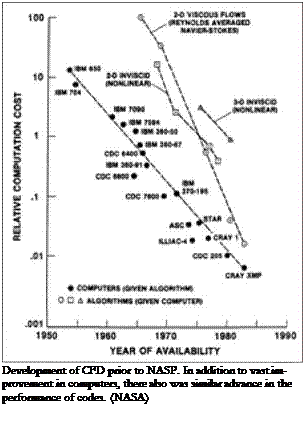Whiteheads point of departure lay in the fundamental equations of fluid flow: the Navier-Stokes equations, named for the nineteenth-century physicists Claude – Louis-Marie Navier and Sir George Stokes. They form a set of nonlinear partial differential equations that contain 60 partial derivative terms. Their physical con­tent is simple, comprising the basic laws of conserva­tion of mass, momentum, and energy, along with an equation of state. Yet their solutions, when available, cover the entire realm of fluid mechanics.2

An example of an important development, contemporaneous with Whiteheads presentation, was a 1985 treatment of flow over a complete X – 24C vehicle at Mach 5.95. The authors, Joseph Shang and S. J. Scheer, were at the Air Forces Wright Aeronautical Laboratories. They used a Cray X-MP supercomputer and gave

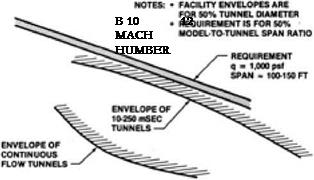
Availability of test facilities. Continuous-flow wind tunnels are far below the requirements of real­istic simulation of full-size aircraft in flight. Impulse facilities, such as shock tunnels, come close to the requirements but are limited by their very short run times. (NASA) cD cL L/D Experimental data 0.03676 0.03173 1.158 Numerical results 0.03503 0.02960 1.183 Percent error 4.71 6.71 2.16

(Source: AIAA Paper 85-1509)

In that year the state of the art permitted extensive treatments of scramjets. Complete three-dimensional simulations of inlets were available, along with two – dimensional discussions of scramjet flow fields that covered the inlet, combustor, and nozzle. In 1984 Fred Billig noted that simulation of flow through an inlet using complete Navier-Stokes equations typically demanded a grid of 80,000 points and up to 12,000 time steps, with each run demanding four hours on a Control Data Cyber 203 supercomputer. A code adapted for supersonic flow was up to a hundred times faster. This made it useful for rapid surveys of a number of candidate inlets, with full Navier-Stokes treatments being reserved for a few selected choices.4

CFD held particular promise because it had the potential of overcoming the limitations of available facilities. These limits remained in place all through the NASP era. A 1993 review found “adequate” test capability only for classical aerody­namic experiments in a perfect gas, namely helium, which could support such work to Mach 20. Between Mach 13 and 17 there was “limited” ability to conduct tests that exhibited real-gas effects, such as molecular excitation and dissociation. Still, available facilities were too small to capture effects associated with vehicle size, such as determining the location of boundary-layer transition to turbulence.

For scramjet studies, the situation was even worse. There was “limited” abil­ity to test combustors out to Mach 7, but at higher Mach the capabilities were “inadequate.” Shock tunnels supported studies of flows in rarefied air from Mach 16 upward, but the whole of the nation’s capacity for such tests was “inadequate.” Some facilities existed that could study complete engines, either by themselves or in airframe-integrated configurations, but again the whole of this capability was “inadequate.”5

Yet it was an exaggeration in 1984, and remains one to this day, to propose that CFD could remedy these deficiencies by computing one’s way to orbital speeds “with high confidence.” Experience has shown that CFD falls short in two areas: prediction of transition to turbulence, which sharply increases drag due to skin fric­tion, and in the simulation of turbulence itself.

For NASP, it was vital not only to predict transition but to understand the prop­erties of turbulence after it appeared. One could see this by noting that hypersonic propulsion differs substantially from propulsion of supersonic aircraft. In the latter, the art of engine design allows engineers to ensure that there is enough margin of thrust over drag to permit the vehicle to accelerate. A typical concept for a Mach 3 supersonic airliner, for instance, calls for gross thrust from the engines of 123,000 pounds, with ram drag at the inlets of 54,500. The difference, nearly 80,000 pounds of thrust, is available to overcome skin-friction drag during cruise, or to accelerate.

At Mach 6, a representative hypersonic-transport design shows gross thrust of

330,0 pounds and ram drag of 220,000. Again there is plenty of margin for what, after all, is to be a cruise vehicle. But in hypersonic cruise at Mach 12, the numbers typically are 2.1 million pounds for gross thrust—and 1.95 million for ram drag! Here the margin comes to only 150,000 pounds of thrust, which is narrow indeed. It could vanish if skin-friction drag proves to be higher than estimated, perhaps because of a poor forecast of the location of transition. The margin also could vanish if the thrust is low, due to the use of optimistic turbulence models.6

Any high-Mach scramjet-powered craft must not only cruise but accelerate. In turn, the thrust driving this acceleration appears as a small difference between two quantities: total drag and net thrust, the latter being net of losses within the engines. Accordingly, valid predictions concerning transition and turbulence are matters of the first importance.

NASP-era analysts fell back on the “eN method,” which gave a greatly simplified sum­mary of the pertinent physics but still gave results that were often viewed as useful. It used the Navier-Stokes equa­tions to solve for the overall flow in the lami – nary boundary layer, upstream of transition. This method then intro­duced new and simple equations derived from the original Navier – Stokes. These were linear and traced the

growth of a small disturbance as one followed the flow downstream. When it had grown by a factor of 22,000—e10, with N = 10—the analyst accepted that transition to turbulence had occurred.7

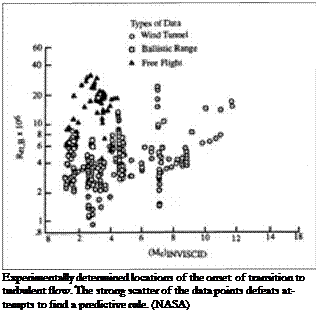
One can obtain a solution in this fashion, but transition results from local rough­nesses along a surface, and these can lead to results that vary dramatically. Thus, the repeated re-entries of the space shuttle, during dozens of missions, might have given numerous nearly identical data sets. In fact, transition has occurred at Mach numbers from 6 to 19! A 1990 summary presented data from wind tunnels, ballistic ranges, and tests of re-entry vehicles in free flight. There was a spread of as much as 30 to one in the measured locations of transition, with the free-flight data showing transition positions that typically were five times farther back from a nose or leading edge than positions observed using other methods. At Mach 7, observed locations covered a range of 20 to one.8

One may ask whether transition can be predicted accurately even in principle because it involves minute surface roughnesses whose details are not known a priori and may even change in the course of a re-entry. More broadly, the state of transi­tion was summarized in a 1987 review of problems in NASP hypersonics that was written by three NASA leaders in CFD:

Almost nothing is known about the effects of heat transfer, pressure gradient, three-dimensionality, chemical reactions, shock waves, and other

influences on hypersonic transition. This is caused by the difficulty of conducting meaningful hypersonic transition experiments in noisy ground – based facilities and the expense and difficulty of carrying out detailed and carefully controlled experiments in flight where it is quiet. Without an adequate, detailed database, development of effective transition models will be impossible.9

Matters did not improve in subsequent years. In 1990 Mujeeb Malik, a leader in studies of transition, noted “the long-held view that conventional, noisy ground facilities are simply not suitable for simulation of flight transition behavior.” A sub­sequent critique added that “we easily recognize that there is today no reasonably reliable predictive capability for engineering applications” and commented that “the reader…is left with some feeling of helplessness and discouragement.”10 A contem­porary review from the Defense Science Board pulled no punches: “Boundary layer transition…cannot be validated in existing ground test facilities.”11

There was more. If transition could not be predicted, it also was not generally possible to obtain a valid simulation, from first principles, of a flow that was known to be turbulent. The Navier-Stokes equations carried the physics of turbulence at all scales. The problem was that in flows of practical interest, the largest turbulent eddies were up to 100,000 times bigger than the smallest ones of concern. This meant that complete numerical simulations were out of the question.

Late in the nineteenth century the physicist Osborne Reynolds tried to bypass this difficulty by rederiving these equations in averaged form. He considered the flow velocity at any point as comprising two elements: a steady-flow part and a turbulent part that contained all the motion due to the eddies. Using the Navier – Stokes equations, he obtained equations for averaged quantities, with these quanti­ties being based on the turbulent velocities.

He found, though, that the new equations introduced additional unknowns. Other investigators, pursuing this approach, succeeded in deriving additional equations for these extra unknowns—only to find that these introduced still more unknowns. Reynolds’s averaging procedure thus led to an infinite regress, in which at every stage there were more unknown variables describing the turbulence than there were equations with which to solve for them. This contrasted with the Navier – Stokes equations themselves, which in principle could be solved because the number of these equations and the number of their variables was equal.

This infinite regress demonstrated that it was not sufficient to work from the Navier-Stokes equations alone—something more was needed. This situation arose because the averaging process did not preserve the complete physical content of the Navier-Stokes formulation. Information had been lost in the averaging. The problem of turbulence thus called for additional physics that could replace the lost information, end the regress, and give a set of equations for turbulent flow in which the number of equations again would match the number of unknowns.12

The standard means to address this issue has been a turbulence model. This takes the form of one or more auxiliary equations, either algebraic or partial-differential, which are solved simultaneously with the Navier-Stokes equations in Reynolds-aver­aged form. In turn, the turbulence model attempts to derive one or more quantities that describe the turbulence and to do so in a way that ends the regress.

Viscosity, a physical property of every liquid and gas, provides a widely used point of departure. It arises at the molecular level, and the physics of its origin is well understood. In a turbulent flow, one may speak of an “eddy viscosity” that arises by analogy, with the turbulent eddies playing the role of molecules. This quantity describes how rapidly an ink drop will mix into a stream—or a parcel of hydrogen into the turbulent flow of a scramjet combustor.13

Like the eN method in studies of transition, eddy viscosity presents a view of tur­bulence that is useful and can often be made to work, at least in well-studied cases. The widely used Baldwin-Lomax model is of this type, and it uses constants derived from experiment. Antony Jameson of Princeton University, a leading writer of flow codes, described it in 1990 as “the most popular turbulence model in the industry, primarily because it’s easy to program.”14

This approach indeed gives a set of equations that are solvable and avoid the regress, but the analyst pays a price: Eddy viscosity lacks standing as a concept supported by fundamental physics. Peter Bradshaw of Stanford University virtu­ally rejects it out of hand, declaring, “Eddy viscosity does not even deserve to be described as a ‘theory’ of turbulence!” He adds more broadly, “The present state is that even the most sophisticated turbulence models are based on brutal simplifica­tion of the N-S equations and hence cannot be relied on to predict a large range of flows with a fixed set of empirical coefficients.”15

Other specialists gave similar comments throughout the NASP era. Thomas Coakley of NASA-Ames wrote in 1983 that “turbulence models that are now used for complex, compressible flows are not well advanced, being essentially the same models that were developed for incompressible attached boundary layers and shear flows. As a consequence, when applied to compressible flows they yield results that vary widely in terms of their agreement with experimental measurements.”16

A detailed critique of existing models, given in 1985 by Budugur Lakshminara – yana of Pennsylvania State University, gave pointed comments on algebraic models, which included Baldwin-Lomax. This approach “provides poor predictions” for flows with “memory effects,” in which the physical character of the turbulence does not respond instantly to a change in flow conditions but continues to show the influ­ence of upstream effects. Such a turbulence model “is not suitable for flows with curvature, rotation, and separation. The model is of little value in three-dimensional complex flows and in situations where turbulence transport effects are important.”

“Two-equation models,” which used two partial differential equations to give more detail, had their own faults. In the view of Lakshminarayana, they “fail to cap­ture many of the features associated with complex flows.” This class of models “fails for flows with rotation, curvature, strong swirling flows, three-dimensional flows, shock-induced separation, etc.”17

Rather than work with eddy viscosity, some investigators used “Reynolds stress” models. Reynolds stresses were not true stresses, which contributed to drag. Rather, they were terms that appeared in the Reynolds-averaged Navier-Stokes equations alongside other terms that indeed represented stress. Models of this type offered greater physical realism, but again this came at the price of severe computational difficulty.18

A group at NASA-Langley, headed by Thomas Gatski, offered words of caution in 1990: “…even in the low-speed incompressible regime, it has not been possible to construct a turbulence closure model which can be applied over a wide class of

flows__ In general, Reynolds stress closure models have not been very successful in

handling the effects of rotation or three-dimensionality even in the incompressible regime; therefore, it is not likely that these effects can be treated successfully in the compressible regime with existing models.”19

Anatol Roshko of Caltech, widely viewed as a dean of aeronautics, has his own view: “History proves that each time you get into a new area, the existing models are found to be inadequate.” Such inadequacies have been seen even in simple flows, such as flow over a flat plate. The resulting skin friction is known to an accuracy of around one percent. Yet values calculated from turbulence models can be in error by up to 10 percent. “You can always take one of these models and fix it so it gives the right answer for a particular case,” says Bradshaw. “Most of us choose the flat plate. So if you cant get the flat plate right, your case is indeed piteous.”20

Another simple case is flow within a channel that suddenly widens. Downstream of the point of widening, the flow shows a zone of strongly whirling circulation. It narrows until the main flow reattaches, flowing in a single zone all the way to the now wider wall. Can one predict the location of this reattachment point? “This is a very severe test,” says John Lumley of Cornell University. “Most of the simple models have trouble getting reattachment within a factor of two.” So-called “k-epsi – lon models,” he says, are off by that much. Even so, NASA’s Tom Coakley describes them as “the most popular two-equation model,” whereas Princeton University’s Jameson speaks of them as “probably the best engineering choice around” for such problems as…flow within a channel.21

Turbulence models have a strongly empirical character and therefore often fail to predict the existence of new physics within a flow. This has been seen to cause difficulties even in the elementary case of steady flow past a cylinder at rest, a case so simple that it is presented in undergraduate courses. Nor do turbulence models cope with another feature of some flows: their strong sensitivity to slight changes in conditions. A simple example is the growth of a mixing layer.

In this scenario, two flows that have different velocities proceed along opposite sides of a thin plate, which terminates within a channel. The mixing layer then forms and grows at the interface between these streams. In Roshko’s words, “a one – percent periodic disturbance in the free stream completely changes the mixing layer growth.” This has been seen in experiments and in highly detailed solutions of the Navier-Stokes equations that solve the complete equations using a very fine grid. It has not been seen in solutions of Reynolds-averaged equations that use turbulence models.22

And if simple flows of this type bring such difficulties, what can be said of hyper – sonics? Even in the free stream that lies at some distance from a vehicle, one finds strong aerodynamic heating along with shock waves and the dissociation, recombi­nation, and chemical reaction of air molecules. Flow along the aircraft surface adds a viscous boundary layer that undergoes shock impingement, while flow within the engine adds the mixing and combustion of fuel.

As William Dannevik of Lawrence Livermore National Laboratory describes it, “There’s a fully nonlinear interaction among several fields: an entropy field, an acoustic field, a vortical field.” By contrast, in low-speed aerodynamics, “you can often reduce it down to one field interacting with itself.” Hypersonic turbulence also brings several channels for the flow and exchange of energy: internal energy, density, and vorticity. The experimental difficulties can be correspondingly severe.23

Roshko sees some similarity between turbulence modeling and the astronomy of Ptolemy, who flourished when the Roman Empire was at its height. Ptolemy repre­sented the motions of the planets using epicycles and deferents in a purely empirical fashion and with no basis in physical theory. “Many of us have used that example,” Roshko declares. “It’s a good analogy. People were able to continually keep on fixing up their epicyclic theory, to keep on accounting for new observations, and they were completely wrong in knowing what was going on. I don’t think we’re that badly off, but it’s illustrative of another thing that bothers some people. Every time some new thing comes around, you’ve got to scurry and try to figure out how you’re going to incorporate it.”24

A 1987 review concluded, “In general, the state of turbulence modeling for supersonic, and by extension, hypersonic, flows involving complex physics is poor.” Five years later, late in the NASP era, little had changed, for a Defense Science Board program review pointed to scramjet development as the single most impor­tant issue that lay beyond the state of the art.25

Within NASP, these difficulties meant that there was no prospect of computing one’s way in orbit, or of using CFD to make valid forecasts of high-Mach engine performance. In turn, these deficiencies forced the program to fall back on its test facilities, which had their own limitations.