Digital Computation Triggers Automated Structural Analysis

In 1946, the ENIAC, "commonly accepted as the first successful high­speed electronic digital computer,” became operational at the University

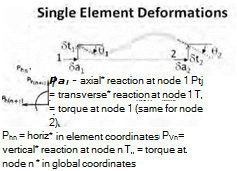
Single Element Reactions

Simple example of discretized structure and single element. NASA.

of Pennsylvania.[800] It took up as much floor space as a medium-sized house and had to be "programmed” by physically rearranging its con­trol connections. Many advances followed rapidly: storing instructions in memory, conditional control transfer, random access memory, mag­netic core memory, and the transistor-circuit element. With these and other advances, digital computers progressed from large and ungainly experimental devices to programmable, useful, commercially available (albeit expensive) machines by the mid-1950s.[801]

The FORTRAN programming language was also developed in the mid-1950s and rapidly gained acceptance in technical communities. This was a "high level language,” which allowed programming instructions to be written in terms that an engineer or analyst could understand; a com­piler handled the translation into "machine language” that the computer could understand. International Business Machines (IBM) developed the original FORTRAN language and also some of the early practical digi­tal computers. Other early digital computers were produced by Control Data Corporation (CDC) and UNIVAC. These developments made it pos­
sible to take the new methods of structural analysis that were emerging and implement them in an automated, repeatable manner.

The essence of these new methods was to treat a structure as a finite number of discrete elastic elements, rather than as a continuum. Reactions (forces and moments) and deflections are only calculated at specific points, called "nodes.” Elements connect the nodes. The stress and strain fields in the regions between the nodes do not need to be solved in the global analysis. They only need to be solved when develop­ing the element-level solution, and once this is done for a particular type of element, that element is available as a prepackaged building block. Complex shapes and structures can then be built up from the simple elements. A simple example—using straight beam elements to model a curved beam structure—is illustrated here.

To find, for example, the relationship between the displacements of the nodes and the corresponding reactions, one could do the following (called the unit displacement method). First, a hypothetical unit dis­placement of one node in one degree of freedom (d. o.f.) only is assumed. This displacement is transposed into the local element coordinate sys­tems of all affected elements. (In the corresponding figure, this would entail the relatively simple transformation between global horizontal and vertical displacements, and element axial and transverse displace­ments. The angular displacements would require no transformation, except in some cases a sign change.) The predetermined element stiff­ness matrices are used to find the element-level reactions. The element reactions are then translated back into global coordinates and summed to give the total structure reactions—to the single hypothetical displace­ment. This set of global reactions, plus zeroes for all forces unaffected by the assumed displacement, constitutes one column in the "stiffness matrix.” By repeating the exercise for every degree of freedom of every node, the stiffness matrix can be built. Then the reactions to any set of nodal displacements may be found by multiplying the stiffness matrix by the displacement vector, i. e., the ordered list of displacements. This entails difficult bookkeeping but simple math.

It is more common in engineering, however, to have to find unknown displacements and stresses from known applied forces. This answer is not possible to obtain so directly. (That is, if the process just described seems direct to you. If it does, you are probably an engineer. If it seems too trivial to have even mentioned, then you are probably a mathematician.)

Instead, after the stiffness matrix is found, it must be inverted to obtain the flexibility matrix. The inversion of large matrices is a sci­ence in itself. But it can be done, using a computer, if one has time to wait. Most of the science lies in improving the efficiency of the process. Another important output is the stress distribution throughout the struc­ture. But this problem has already been solved at the element level for a hypothetical set of element nodal displacements. Scaling the generic stress distribution by the actual displacements, for all elements, yields the stress state throughout the structure.

There are, of course, many variations on this theme and many com­plexities that cannot be addressed here. The important point is that we have gone from an insoluble differential equation to a soluble matrix arithmetic problem. This, in turn, has enabled a change from individual analyses by hand of local portions of a structure to a model­ing effort followed by an automated calculation of the stresses and deflec­tions of the entire structure.

Pioneering papers on discretization of structures were published by Alexander Hrennikoff in 1941 at the Massachusetts Institute of Technology and by Richard Courant in 1943 at the mathematics institute he founded at New York University that would later bear his name. These papers did not lead to immediate application, in part perhaps because they were ahead of the necessary computational technology and in part because they were still somewhat theoretical and had not yet developed a well – formed practical implementation. The first example of what we now call the finite element method (FEM) is commonly considered to be a paper by M. J. Turner (Boeing), R. W. Clough (University of California at Berkeley, Civil Engineering Department), H. C. Martin (University of Washington, Aeronautical Engineering Department), and L. J. Topp in 1956.[802] This paper presented a method for plane stress problems, using triangular elements. John Argyris at the University of Stuttgart, Germany, also made impor­tant early contributions. The term "finite element method” was actually coined by Clough in 1960. The Civil Engineering Department at Berkeley became a major center of early finite element methods development.[803]

By the mid-1960s, aircraft companies, computing companies, univer­sities, and Government research centers were beginning to explore the possibilities—although the method allegedly suffered some initial lack of interest in the academic world, because it bypassed elegant mathe­matical solutions in favor of numerical brute force.[804] However, the prac­tical value could not long be ignored. The following insightful comment, made by a research team at the University of Denver in 1966 (working under NASA sponsorship), sums up the expectation of the period: "It is certain that this concept is going to become one of the most important tools of engineering in the future as structures become more complex and computers more versatile and available.”[805]