Heady Days

When interesting things like this come up, many of the most important results come out of people’s curiosity, just following up something, and someone over in a corner who is not sup­posed to be doing anything about it usually comes out with the best answers.

—Homer Newell, science programs coordinator for Vanguard, discussing Sputnik at a meeting of the IGY’s Technical Panel on Earth Satellites, October 22, 1957

W

hen Wall Street opened on Monday, investors scrambled to buy stock in companies connected with missile programs, abandoning other issues and pushing prices to their lowest level in two years.

Two hundred miles to the south in Washington D. C., there was another scramble as the Naval Research Laboratory briefed President Eisenhower and congressional members on the status of Vanguard. James Lay, executive secretary of the National Security council, called the head of the National Science Foundation, Alan Waterman. The status of the U. S.’s satellite plans, Lay said, would be second on the agenda at Thursday’s security council meeting, immediately after a CIA presentation about Soviet defenses. Later that day, Lay called Waterman again; discussion of the U. S. satellite had, he said, now moved to the top of the agenda.

As for the general public, the Saturday morning papers greeted any­one who still did not know of the launch with three-deck banner head­lines. Sputnik squeezed reporting of the drama surrounding desegregation in Little Rock and Jimmy Hoffa’s election as president of the Teamsters Union into a corner of the front page of the New York Times. By Sunday, nothing short of a declaration of war could have rivaled the satellite’s edi­torial supremacy. And a Times editorial stated soberly, “It is war itself rather than any designated enemy against which we must now defend ourselves.” At his home near the Applied Physics Laboratory, Bill Guier tuned in to every radio and TV broadcast. He was thirty-one, a theoretical physicist, and a news junky even in less exciting times. That weekend, Guier was as fascinated as the rest of the country He had no idea that the satellite would change his future.

Nor did George Weiffenbach, then a thirty-six-year-old experimen­tal physicist. He too learned during the weekend of the launch of the satellite. Weiffenbach recalls that he was not particularly excited. His wife says otherwise and remembers eager calls to friends and colleagues.

On Monday afternoon, October 7, Guier and Weiffenbach unknow­ingly took their first steps in the development of a new method of orbital determination and prediction.

Orbital mechanics—the behavior of satellites in orbit—lies at the heart of space exploration. Without a detailed and accurate knowledge of the subject, man-made satellites would be useless, because no one would know where they were or were likely to be. And no one would know the time and posi­tion at which a satellite instrument made an interesting observation, such as of an atmospheric disturbance with the makings of a hurricane. Yet it is impractical to follow all satellites throughout their orbits. Hence observa­tions are made of part of the orbit and that information feeds into the math­ematical relationships that describe behavior in orbit. Once the orbit is determined, the satellite’s future behavior—its position at given times—can be predicted. Orbital predictions allow mission planners to determine, say, when the space shuttle should lift off if it is to dock with the Mir space sta­tion. They allowed the operators of the Transit navigation satellites to calcu­late exactly where the spacecraft would be at every two-minute interval in their orbits, thus providing navigators with a reliable celestial fix.

All of the groups observing Sputnik—amateurs and professionals alike—were tackling the problem of its motion within the framework of classical physics laid down over the previous three centuries by the likes of Johannes Kepler (working with Tycho Brahe’s data), Galileo Galilei, and Isaac Newton.

Brahe (1546 — 1601) was an astronomer who in the days before tele­scopes designed and built instruments that enabled him to measure the angles to heavenly bodies. His story is well known in the annals of science because he recognized the importance of basing theory on accurate obser­vations rather than philosophical speculation. His observations of the orbit of Mars were invaluable to Kepler (1571 — 1630) when Kepler was seeking a fundamental description of planetary motion.

Kepler assumed, though this was far from generally accepted at the time, that Copernicus had been correct in asserting that the planets moved around the sun. With this assumption, Kepler explored numerous mathe­matical models, seeking one that would lead to a description of planetary motion consistent with Brahe’s data.

Kepler’s belief in the integrity of Brahe’s data kept him at his calcula­tions through years of poverty and illness, calculating and recalculating until finally, theory was consistent with observation. Kepler found that to fit Brahe’s observations, the planets must move in ellipses—a geometric figure that has two foci; in the case of Earth-orbiting satellites, one focus of the satellite’s orbit is the center of mass of the earth. Kepler next described in a mathematical relationship how a body in orbit sweeps out equal areas of an ellipse in equal times. In a third law, he described how planetary orbits relate to one another mathematically.

In reaching these conclusions Kepler was forced to burn his intellec­tual bridges, cutting himself off from both views of the universe that were accepted in his day. First, by accepting the Copernican assumption, he was no longer in sympathy with the Catholic Church; second, he had given up the Greek view of the planets moving in circles. This second view was particularly hard for Kepler to abandon. Indeed, it was a view that Galileo was never able to abandon.

At one stage, Kepler thought that the orbits might be circular, but when he made calculations based on this assumption there was a small dis­crepancy with Brahe’s data that kept him at his calculations until he finally concluded that the planetary orbits are elliptical. With less confidence in Brahe, Kepler could easily have stopped his laborious calculations before reaching his fundamental insight.

Kepler was ecstatic. Soon after he formulated the last of the three laws that bear his name, he wrote, “Nothing holds me; I will indulge my sacred fury…. If you forgive me, I rejoice; if you are angry, I can bear it; the die is cast, the book is written, to be read either now or by posterity, I care not which….”

Though Galileo (1564-1642) never accepted elliptical orbits, his giant strides in mechanics provided, along with Kepler’s work, a solid sci­entific basis for Isaac Newton (1642— 1727). Among other things, Newton discerned and formulated the all-important law that force is equal to mass times acceleration. All of the different methods of observing the satellite’s position, Guier’s and Weiffenbach’s included, sought different ways to gather information that could make use of this law—the so-called second law of motion—within the concept of orbits established by Kepler.

Newton’s second law (F = MA) and Kepler’s second law allow math­ematicians to deduce six numbers that give an approximate description of an orbit. In tribute, these numbers—or elements—are named after Kepler. One gives the orbit’s shape, that is, how elliptical it is, whether it is extremely elongated or close to circular. This element, termed eccentric­ity, is defined as the distance between the two foci divided by the length of the major axis. The closer the value of eccentricity is to one, the more elliptical the orbit. An eccentricity of zero describes a circle.

A second element, the semimajor axis, gives the size of the orbit. Two more describe the orbit’s orientation in three dimensions with respect to the celestial sphere, and a fifth pinpoints that orientation with respect to the earth (respectively, inclination, ascending node, and argument of perigee). The sixth element is the time at which the satellite is at the ascending or the descending node, that is, the time at which the satellite crosses the plane of the equator heading either north or south. It is more usual to use the ascending node.

Kepler’s elements, however, are only averages. Any additional force, such as an inhomogeneity in the earth’s gravitational field, that acts on the satellite causes it to deviate from the average path described by Kepler’s elements. The deviation might be small and local or might cause the entire orbit to precess; that is, the orbit can rotate about an axis in such a way as to sweep out a conical shape. Thus a description of a satellite in near-Earth orbit requires eight parameters: the six Keplerian elements and two preces­sion terms. While such a description is more accurate than that provided by the Keplerian elements alone, it is still only an approximation. Only by giving the positional coordinates at given times can an accurate orbit be described, and this is what the Transit team eventually did.

On Monday, October 7, people were still struggling simply to observe Sputnik. The Minitrack stations were being adapted; only some of the Baker-Nunn cameras were in place; the first confirmed Moonwatch sightings, in Woomera and Sydney, Australia, would not be made until the next day.

Across the ocean in England, at Jodrell Bank and the Royal Aircraft Establishment, radio telescopes were waiting for Sputnik. They tracked the satellite by keeping its signal at the focus of their dishes, and the angle of the telescope relative to a fixed north-south line and to the horizon gave respectively the azimuth and elevation of the satellite. These data can be used to determine the Kepler elements. When in April 1958 Guier and Weiffenbach published a brief summary of their methods and results in scientific correspondence to the journal Nature, they compared the orbit they calculated for Sputnik I with those from Jodrell Bank and the RAE. There was good agreement.

Once their technique was developed, Guier and Weiffenbach’s orbital determination could, unlike those from Minitrack and the Smithsonian Astrophysical Observatory, be based on observations from a single satellite pass. Eventually, for truly accurate orbital determinations their technique would be applied to the observations collected by many ground stations over a twelve to eighteen hour period. When reversed, the technique allowed position to be fixed at a receiver on Earth from one satellite pass, the basis of Transit.

As Guier and Weiffenbach made their separate ways to work that Monday, all this was shrouded in the future. They knew each other slightly as fellow members of the research center. They had worked together on some of the same projects during the previous few years. By chance, that Monday they ate lunch at the same table in the canteen. Just as at the White House and the Pentagon, Sputnik was the focus of conversation.

Guier thought the satellite was superb. Yet his history was not one that obviously suggested an admirer of Soviet ingenuity. As a graduate stu­dent in the late 1940s, he had heard Edward Teller, “father of the hydrogen bomb,” call for physicists to fight a new kind of technological war. In a world newly afraid of atomic power and rife with the political tensions that would lead to the Berlin Wall, Teller’s call to arms seemed logical to Guier. Guier joined APL’s research center in 1951.

Like Guier, Weiffenbach believed in the importance of weapons research and in the protection that technological supremacy could afford. He had been in Europe during the war and had been among those waiting in the summer of 1945 for orders to go to the Pacific. On his demobiliza­tion, the government paid for his education, something his parents could not have afforded to do, through the provisions of the GI Bill. It seemed right to Weiffenbach to work to strengthen national security, both because of what he had seen in Europe and to repay the nation for his education.

Guier’s choice had a consequence that, though small in the scheme of things, was indicative of the times. He had a German friend behind the

Iron Curtain. Their correspondence helped Guier with the language stud­ies necessary for his doctorate. Guier did not see this man through a polit­ical lens, and he was staggered when his thesis director advised him to end the correspondence. The Soviets might exploit the relationship, said the professor, and even if they didn’t, the letters could damage Guier’s career.

At first Guier ignored the advice, but a summer internship at Los Alamos changed his mind. Assigned to work on computer models of nuclear explosions, he learned of the secrecy surrounding nuclear weapons, of the comparative simplicity of some of the physics, and the great fear in government circles that the Soviets would soon have similar technology. These fears were heightened when the Klaus Fuchs and Rosenberg scandals erupted. Fuchs, a British physicist, and Julius and Ethel Rosenberg, an American couple, gave atomic secrets to the Soviets. Fuchs was imprisoned, the Rosenbergs executed. In this climate, Guier became acutely aware of the Cold War and reluctantly ended his correspondence.

Accepting the political realities of their world, Guier and Weiffen- bach settled down to conduct basic research in support of weapons sys­tems. The Soviets were the enemy.

And yet…

Here was something new, the first foothold in space. The lunch group asserted, with the scientist’s classic understatement, that Sputnik was not trivial. APL staff, deeply involved in missile and radar work, knew this well. And despite its provenance, Sputnik was intriguing.

The lab was not involved with the IGY. Thus people at APL, cer­tainly at Guier’s and Weiffenbach’s low level, had no inside track to what little was known about Sputnik. Nor was there any involvement with the planning for Minitrack. Their ignorance of the IGY’s discussions about the limitations of Doppler and the advantages of interferometry freed Guier and Weiffenbach from the conventional wisdom about satellite tracking and orbital analysis and ultimately stood the pair in good stead.

Lunch wound down.

Guier and Weiffenbach decided to rectify the surprising fact that in a lab bristling with antennas and receivers nobody was listening to Sputnik’s signal. That was all: an indulgence of curiosity. They did not intend to make a serious attempt to determine and predict Sputnik’s orbit, but only to calculate roughly when the satellite would reappear over Washington.

When he got back to his lab, Weiffenbach attached a wire to the back of a receiver and prepared to tune in. He knew—how, given the wide­spread publicity, could he not—that Sputnik was broadcasting an intermit­tent signal at about twenty megahertz.

Serendipity, that great friend to science, now lent a hand for the first time. Weiffenbach’s receiver, working on the same principle as any ham radio operator’s equipment, added the satellite signal of approximately twenty megahertz to a reference frequency of twenty megahertz, resulting in an audible “beat” note—Sputnik’s distinctive beep beep. But Weiffen­bach’s reference frequency was special; it was broadcast by the nearby National Bureau of Standards as a service to scientific laboratories, and it was at a precise twenty megahertz.

Some few hours later, when their rampant curiosity turned slowly to a controlled scientific interest, Guier and Weiffenbach started recording the beat frequency along with the national time signal during each pass of the satellite from horizon to horizon. And that was the raw data from which they developed a new technique for orbital analysis and provided the sci­entific underpinning for a satellite navigational system. Without a precise reference signal, they could not have extracted the information they did. Had the reference signal been broadcast from a more distant site, its quality would have been degraded on passage through the atmosphere, and again they could not have extracted the information they did.

As they waited for the satellite to come over the horizon, Weiffen­bach fiddled with the knobs of his receiver. The airwaves were buzzing. Disembodied voices mimicked the satellite’s signal. Others repeated, “this is your Sputnik … this is your Sputnik.” Then—faintly—Weiffenbach picked up an English-language broadcast from Moscow. It gave the times when the satellite would be over the world’s capitals. They knew when to listen.

By now a crowd had gathered. During the next few days there would at times be so many people in the lab that Weiffenbach could scarcely squeeze through to his receiver. As they waited, there were a few mur­murs, not serious, that perhaps the signal was a fake. Most wondered whether the signal would carry information; measurements, perhaps, of the satellite’s temperature—the first remote measurements (telemetry— measurement at a distance) from space.

The same question arose at a meeting of the IGY’s satellite panel on October 22. Inevitably, the main topic on the agenda was a discussion of when America would be ready to launch its own satellite. But the panel also discussed, without reaching a conclusion, whether it could squeeze money from the budget to analyze Sputnik’s signal for telemetry Bill Pick­ering said that even if the signal did carry temperature or pressure mea­surements, they would be useless without knowing how the Soviet instru­ments were calibrated. Homer Newell observed that maybe someone unconnected with the IGY’s work would decipher Sputnik’s message. (The Soviets had said, incidentally, that there would be no telemetry from their first satellite.)

The discussion was academic: Sputnik stopped transmitting a few days after that meeting. And long before October 22, Weiffenbach and Guier had concluded that there was no telemetry.

In Weiffenbach’s lab, the crowd heard Sputnik’s beep for the first time late on Monday afternoon. Guier, an amateur musician with good relative pitch, cocked an ear. Surely the pitch of the beat note was changing. Of course, he said, it must be the Doppler shift. The change was subtle, a mat­ter of about an octave over twenty minutes. It was this phenomenon, known to every physics student, that was to provide the key to the Applied Physics Laboratory’s work on geodesy and Transit.

The Doppler shift is, at heart, conceptually quite easy to grasp. Its consequences can reveal much about the natural world. Astronomers, for example, find it of great utility when studying the motion of stars. But, as with much else in physics, once one goes beyond the basic description of a phenomenon, things become complicated, and the Doppler effect is not easy to exploit in the real world. For this reason, some mistrusted Guier’s and Weiffenbach’s work. Others were suspicious of their mathematical analysis. The two scientists, recalled Guier, would be told “reliably” what criticism this scientist or another had made of their work and were all but told they were cheating.

A straw poll soliciting descriptions of the Doppler effect elicited com­ments ranging from the general statement that it has to do with the way the sound of a car’s engine changes, to the statement that frequency increases as a source moves toward you and decreases as it moves away. Given its importance to Transit and the understandable vagueness of many, it seems worth describing the basic concept in some detail.

The Doppler shift, which is a consequence of a moving frequency source, is usually introduced to unsuspecting physics students through a discussion of how and why the pitch of a train’s whistle changes as the train races past. It is pointed out that the change in pitch occurs even though the pitch of the whistle would not be changing if you were sitting next to it on the train’s roof.

I’d prefer to start at the seaside, and to tackle the train analogy later.

Imagine facing the ocean for twenty seconds and counting the waves as they crash into you. Now imagine walking into the ocean to meet the waves head on. More waves will reach you in those twenty seconds than if you had stood still. Now imagine walking out of the ocean directly away from the waves, and you can see that fewer crests will reach you in twenty seconds than if you had remained stationary. So the number of waves gen­erated by the ocean in a given amount of time (the transmitter frequency) remains constant, but the number of wave crests encountered (received frequency) increases or decreases because of your motion relative to the waves. The difference between the transmitter frequency (ocean waves rolling in per second) and the received frequency (wave crests encoun­tered) can be thought of as the Doppler frequency—the amount by which the received frequency differs from the transmitter frequency because of relative motion between a frequency source and a receiver.

Now imagine that the ocean is unnaturally well behaved and that the wave crests are spaced evenly (the transmitter frequency is constant). You are walking into the ocean at a steady pace. In the first twenty seconds you encounter a certain number of wave crests. If your pace and direction for­ward stay the same, how many wave crests do you encounter in the next twenty seconds compared with the first twenty seconds?

The same number, of course, because nothing about the ocean waves or about your motion with respect to them has changed between the con­secutive twenty-second intervals. So the frequency received, which was Doppler-shifted upwards by your initial motion forward, remains constant. A graph of received frequency against time would be a straight line parallel to the horizontal, or x-axis. When you turn around and retrace your steps at exactly the same pace, the frequency received will be Doppler-shifted downwards and will remain constant at that value. A graph of received fre­quency against time would also be a straight line parallel to the x-axis, but this time at a value below the transmitter frequency. Momentarily, as you stop and turn, you will be buffeted by waves at the natural frequency of the ocean.

Once you make it to dry land, turn back to the waves. They are now behaving in a very peculiar way The wave fronts are aligned exactly paral­lel to one another, wave crests evenly spaced. They roll in at a rate of 100 per second. You walk directly into them, along a path perpendicular to the wave front. You are walking at a pace which in one second permits you to cover a distance equal to six wavelengths. So in one second you encounter 106 wave crests. (Transmitter frequency is 100 waves per second, or cycles per second; the received frequency is 106 cycles per second and the Doppler frequency is 6 cycles per second.)

Now instead of walking a path perpendicular to the wave front, walk into the ocean at a slant. The number of waves crests you encounter in a second will still be greater than if you stood still (will be Doppler shifted upwards), but it will not be as great as if you took the perpendicular path. The received frequency and whether or not it is shifted upwards or down­wards and by how much depends on the relative motion between you and the wave front. See the diagram below.

The same logic can be applied to the sound waves of a train’s whistle and to radio waves from a satellite.

Let’s take the train. If you and the train remain stationary, the number of sound waves emitted by its whistle in a given time is the number that you hear in that time, just as the number of waves rolling ashore in a given time interval was equal to the number of wave crests that hit you when you stood still.

If you are standing on the track and the train is moving directly towards you at a constant speed, the rate at which the range between you and the train changes remains constant just as when you were moving into the water along a path perpendicular to the wave front at a pace of six
wavelengths per second. So the frequency received from the train’s whistle is shifted upwards because of forward motion and remains constant at the new value as long as that relative velocity (speed and direction) remain constant. Then as the whistle moves through you, for a moment you hear the natural frequency of the whistle (the Doppler shift is zero). Then the train moves away and the frequency is Doppler shifted downwards, and that Doppler shift also remains constant while the relative velocity remains constant. This is all logically equivalent to what happens as you walk in, turn, and walk out of the ocean.

Now what happens if you are standing off at some distance on one side of the track? The rate at which the distance between you and the train changes is no longer constant. That is, the relative velocity between you and the source is no longer constant. So the Doppler shift is no longer constant.

The diagrams below, where marks on the track represent the train’s position at, say, fifteen-second intervals, show how the rate of change of distance between train and observer changes with time, and how that change depends on how close the listener is to the track.

Again there is a logical equivalence between walking into the ocean at a constant angle or changing the angle as you walk into the waves. Thus, the amount by which the Doppler frequency is shifted above the transmit­ter frequency decreases gradually as the train moves towards you, until at the point of closest approach the received frequency is affected neither by the forward nor retreating motion of the train. Afterwards, the frequency con­tinues to decrease.

Graphs of received frequency against time would look like those in the next two diagrams.

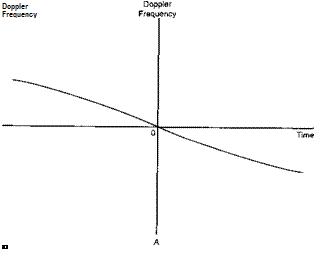The observer is further away from the track in the example below com­pared with the one above. If you look at the way distance is changing with time in the train diagrams, that is, at the way the relative velocity changes with time, the graphs make sense. This relative velocity, on which the Doppler shift depends, changes less the further away the moving source remains from the listener. Hence the change in frequency is less pro­nounced in the diagram below.

Sputnik was in motion, so its transmission was Doppler-shifted. Unlike the train whistle of our example, however, the frequency arriving at the lab was way outside the range of human ears. Instead, the received frequency was combined with a reference signal to give a “beat” signal in the audible range. Guier’s musician’s ear detected changes in the beat frequency as a change in pitch.

Many amateur listeners who heard the phenomenon dismissed it as receiver drift. Guier and Weiffenbach did not, first, because they were physicists listening to a moving frequency source and the concept of Doppler shifting was probably hovering not too far from conscious thought; second, they both knew that they had a good reference source and that Weiffenbach’s experimental experience would have enabled him to recognize receiver drift or the consequences of a poor reference source for what it was.

Before Guier and Weiffenbach heard the Doppler shift, they were lis­tening to Sputnik out of the same curiosity that drove the Moonwatchers and the rest of the country. Once they recognized the Doppler shift, they became more serious.

As Sputnik’s beep faded over their horizon for the first time, they decided to record the sound of the Doppler shift simultaneously with the national time signal. Although they had no particular idea of what they would do with the recordings, they knew that those beeps, which were exciting imaginations across the world, would give them the scientist’s bread and butter: data. And with application and imagination, data can become information.

Another pass was to occur that night. Guier went home to collect a high-quality tape recorder he had recently bought. Back in the lab, Weif­fenbach tuned in well before the satellite appeared. They wanted to collect the complete Doppler shift resulting from a pass from horizon to horizon. During the remaining two and a half weeks that Sputnik transmitted, they recorded the Doppler shift every time the orbit carried the spacecraft within range of the lab. And thus the Soviets provided the experimental setup that was the first step to enabling the Polaris submarines to fix their position at sea more accurately and opened the way to a global naviga­tional system.

Serendipity, in the form of timing and human relationships, now made its second appearance. Weiffenbach, the experimentalist, and Guier, the theoretician, found they worked well together. Experimental and the­oretical physicists, and this is something of an understatement, do not always see eye to eye. During the coming six months, the two men’s skills and outlooks would mesh, gearing up their productivity In later years as they got to know one another better and were part of the team developing Transit, they would have their offices close together so that they could more easily discuss the problems they encountered.

Sputnik’s launch came at the right time for both men. Each was ready for a new project. Guier was feeling a new-found confidence, having emerged recently from chairing an APL committee doing technical work on long-range missile guidance systems for the president’s Science Advi­sory Committee. Weiffenbach had things to prove. He had been scooped twice, once on work for his doctorate.

By Tuesday, Guier and Weiffenbach knew that there was no teleme­try, but they had the recordings. With these they intended to calculate roughly when the satellite would next appear over their horizon. To esti­mate the satellite’s next appearance, they decided to apply physics in the way that the lab had when designing the proximity fuze which detonates a shell on its closest approach to a target. All they needed to do was to find the distances at the point of closest approach between the satellite and the lab—the point where the Doppler frequency was zero—during several passes. If they found these distances, they would have enough data to determine approximate values for the Keplerian elements and to pre­dict roughly when a satellite in that orbit would next be at its closest to the lab.

In taking this approach, Guier and Weiffenbach were applying physics in a well-known way, but the difficulties they encountered were to lead to an innovative interpretation of the Doppler data.

Given APL’s previous work with proximity fuzes, perhaps it was inevitable that Guier and Weiffenbach should have started as they did. An artillery shell emits a radio signal that is reflected from the surface of the target. At the point when the shell has made its closest approach to the tar­get and begins moving away, the Doppler shift is zero and the fuze deto­nates the shell. The technique was important, too, to the lab’s missile work. Missiles would telemeter the Doppler-shifted radio signals that were reflected from the target back to APL’s engineers, who would analyze them to ascertain how closely the missile had approached its target.

Guier’s and Weiffenbach’s first step, therefore, was to turn their recordings into the tables of frequency versus time needed to plot a graph of the satellite’s Doppler shift, because the information from that graph, the Doppler curve, was needed in the equation to find the distance when the satellite was closest to the lab (in missile parlance—the miss distance).

Today, and indeed not too long after Weiffenbach and Guier began their work, automated equipment, the inner mysteries of about which the scientist need not be concerned with, would have done the job. That October, Weiffenbach operated the equipment—a wave analyzer—manu­ally. It was standard equipment, and the natural frequency of the electrical circuits it contained could be adjusted by hand. When a frequency on a recording coincided with that of the analyzer’s circuitry, the analyzer would record a spike. All of the recordings were fed through by hand and the circuitry adjusted laboriously until fifty values of frequency and time had been extracted for each pass.

Sometime early in the process, Guier and Weiffenbach had been joined by two engineers, Harry Zinc and Henry Elliott. Zinc had also been keen to listen to Sputnik. Unknown to Guier and Weiffenbach, he and Elliott had put together equipment with a moderate-gain antenna that was capable of providing a stronger signal than that obtained by the wire attached to Weiffenbach’s receiver.

The four took turns with the tedious job of turning the recordings into tables of frequency and time. An unglamorous task, but an essential part of the scientist’s life—data reduction.

Work began in earnest on Tuesday, October 8. Very quickly, things began to look ambiguous and complicated. Eventually, from this confusion came the idea that led the scientists to being able to determine an orbit from a single satellite pass—the idea that, when turned on its head, was the basis for the Transit system.