ACADEMIC SCIENCE DISCOVERS THE AIRPLANE

Between 1891 and 1896, Otto Lilienthal in Germany made over 2000 successful glider flights. His work was timed perfectly with the rise of photography and the printing industry. In 1871 the dry-plate negative was invented, which by 1890 could freeze a moving object without a blur. Also, the successful halftone method of printing had been developed. As a result, photos of Lilienthal’s flights were widely distributed, and his exploits frequently described in periodicals throughout Europe and the US.

These flights caught the attention of Nikolay Joukowski (Zhukovsky) in Russia. Joukowski was head of the Department of Mechanics at Moscow University when he visited Lilienthal in Berlin in 1895. Very impressed with what he saw, Joukowski bought a glider from Lilienthal, one of only eight that Lilienthal ever managed to sell to the public. Joukowski took this glider back to his colleagues and students in Moscow, put it on display, and vigorously examined it. This is the first time that a university-educated mathematician and scientist, and especially one of some repute, had become closely connected with a real flying machine, literally getting his hands on such a machine. Joukowski did not stop there. He was now motivated about flight – he had actually seen Lilienthal flying. The idea of getting up in the air was no longer so fanciful – it was real. With that, Joukowski turned his scholarly attention to the examination of the dynamics and aerodynamics of flight on a theoretical, mathematical basis. In particular, he directed his efforts towards the calculation of lift. He envisioned bound vortices fixed to the surface of the airfoil along with the resulting circulation that somehow must be related to the lifting action of the airfoil.

Finally, in 1906 he published two notes, one in Russian and the other in French, in two rather obscure Russian journals. In these notes he derived and used the following relation for the calculation of lift (per unit span) for an airfoil:

L = pVT

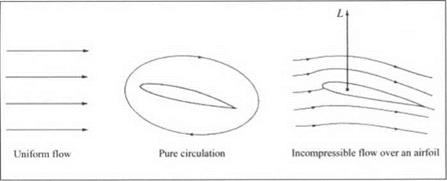
where L is the lift, p is the air density, V is the velocity of the air relative to the airfoil, and Г is the circulation, a technically-defined quantity equal to the line integral of the flow velocity taken around any closed curve encompassing the airfoil (Circulation has physical significance as well. The streamline flow over an airfoil can be visualized as the superposition of a uniform freestream flow and a circulatory flow; this circulatory flow component is the circulation. Figure 1 is a schematic illustrating the concept of circulation.) With this equation, Joukowski revolutionized theoretical aerodynamics. For the first time it allowed the calculation of lift on an airfoil with mathematical exactness. This equation has come down through the twentieth-century labeled as the Kutta-Joukowski Theorem. It is still taught today in university-level aerodynamics courses, and is still used to calculate lift for airfoils in low-speed flows.

The label of this theorem is shared with the name of Wilhelm Kutta, who wrote a Ph. D. dissertation on the subject of aerodynamic lift in 1902 at the University of Munich. Like Joukowski, Kutta was motivated by the flying success of Lilienthal. In particular, Kutta knew that Lilienthal had used a cambered airfoil for his gliders, and that, when cambered airfoils were put at a zero angle of attack to the freestream, positive lift was still produced. This lift generation at zero angle of attack was counter-intuitive to many mathematicians and scientists at that time, but experimental data unmistakenly showed it to be a fact. Such a mystery made the theoretical calculation of lift on a cambered airfoil an excellent research topic at the time – one that Kutta readily took on. By the time he finished his dissertation in 1902, Kutta had made the first mathematical calculations of lift on cambered airfoils. Kutta’s results were derived without recourse to the concept of circulation.

Figure 1. The synthesis of the flow over an airfoil by the superposition of a uniform flow and a circulatory flow.

Only after Joukowski published his equation in 1906 did Kutta show in hindsight that the essence of the equation was buried in his 1902 dissertation. For this reason, the equation bears the name, the Kutta-Joukowski Theorem.

This equation became the quantitative basis for the circulation theory of lift. For the first time a mathematical and scientific understanding of the generation of lift was obtained. The development of the circulation theory of lift was the first major element of the evolution of aerodynamics in the twentieth century, and it was in the realm of science. The objective of Kutta and Joukowski – both part of the academic community – was understanding the nature of lift, and obtaining some quantitative ability to predict lift. Their work was not motivated, at least at first, by the desire to design a wing or airfoil. Indeed, by 1906 wings and airfoils had already been designed and were actually flying on piloted machines, and these designs were accomplished without the benefit of science. The circulation theory of lift was created after the fact.

Contemporary with the advent of the circulation theory of lift was an equally if not more important intellectual breakthrough in the understanding and prediction of aerodynamic drag. The main concern about the prediction of lift on a body inclined at some angle to a flow surfaced in the nineteenth-century, beginning with George Cayley’s concept of generating a sustained force on a fixed wing. In contrast, concern over drag goes all the way back to ancient Greek science. The retarding force on a projectile hurtling through the air has been a major concern for millenniums. Therefore, it is somewhat ironic that the breakthroughs in the theoretical prediction of both drag and lift came at almost precisely the same time, independent of how long the two problems had been investigated.

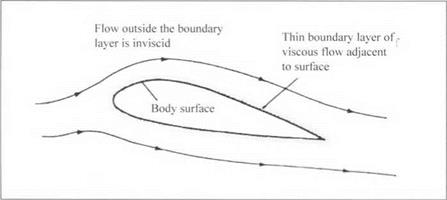
What allowed the breakthrough in drag was the origin of the concept of the boundary layer. In 1904, a young German engineer who had just accepted the position as professor of applied mechanics at Gottingen University, gave a paper at the Third International Mathematical Congress at Heidelberg that was to revolutionize aerodynamics.7 Only eight pages long, it was to prove to be one of the most important fluid dynamics papers in history. In it, Prandtl described the following concept. He theorized that the effect of friction was to cause the fluid immediately adjacent to the surface to stick to the surface, and that the effect of friction was felt only in the near vicinity of the surface, i. e., within a thin region which he called the boundary layer. Outside the boundary layer, the flow was essentially uninfluenced by friction, i. e., it was the inviscid, potential flow that had been studied for the past two centuries. This conceptual division of the flow around a body into two regions, the thin viscous boundary layer adjacent to the body’s surface, and the inviscid, potential flow external to the boundary layer (as shown in Figure 2), suddenly made the theoretical analysis of the flow much more tractable. Prandtl explained how skin friction at the surface could be fundamentally understood and calculated. He also showed how the boundary layer concept explained the occurrence of flow separation from the body surface – a vital concept in the overall understanding of drag. Since 1904, many aerodynamicists have spent their lives studying boundary-layer phenomena – it is still a viable area of research

today. This author dares to suggest that PrandtTs boundary layer concept was a contribution to science of Nobel prize stature. Perhaps one of the best accolades for Prandtl’s paper was given by the noted fluid dynamicist Sydney Goldstein who was moved to state in 1969 that: “The paper will certainly prove to be one of the most extraordinary papers of this century, and probably of many centuries.”8

As in the case of Kutta and Joukowski, Prandtl was a respected member of the academic community, and with the boundary layer concept he made a substantial scientific contribution to aerodynamics. This was science; the boundary layer concept was an intellectual model with which Prandtl explained some of the fundamental aspects of a viscous flow. However, within a few years this concept was being applied to the calculations of drag on simple bodies by some of PrandtTs students at Gottingen, and by the 1920s, research on boundary layers had become focused on acquiring knowledge for the specific purpose of drag calculations on airfoils, wings, and complete airplanes. That is, boundary layer theory became more of an engineering science.

In retrospect the beginning of the twentieth-century was the time of major technological breakthroughs in theoretical aerodynamics. These events heralded another breakthrough – one of almost a sociological nature. Wilhelm Kutta, Nikolay Joukowski, Ludwig Prandtl were all university-educated with Ph. D.s in the mathematical, physical, and/or engineering sciences and all conducted aerodynamic research focused directly on the understanding of heavier-than-air flight. This represents the first time when very respected academicians embraced the flying machine; indeed, the research challenges associated with such machines absolutely dictated the direction of their research. Kutta, Joukowski, and Prandtl were very much taken by the airplane. What a contrast with the prior century, when respected academicians essentially eschewed any association with flying machines, thus

Figure 2. PrandtTs concept of the division of the flow field into two regions: (1) the thin viscous boundary layer adjacent to the body surface, and (2) the inviscid (frictionless) flow outside the boundary layer.

causing a huge technology transfer gap between nineteenth-century science and the advancement of powered flight.

What made the difference? The answer rests in that of another question, namely, who made the difference? The answer is Lilienthal and the Wright brothers. Otto LilienthaTs successful glider flights were visual evidence of the impending success of manned flight; we have seen how the interest of both Kutta and Joukowski was motivated by watching Lilienthal winging through the air, as seen either via photographs or by actual observation. And when the news of Wilbur’s and Orville’s success with the Wright Flyer in 1903 gradually became known, there was no longer any doubt that the flying machine was a reality. Suddenly, work on aeronautics was no longer viewed as the realm of misguided dreamers and madmen; rather it opened the floodgates to a new world of research problems, to which twentieth-century academicians have flocked. After this, the technology transfer gap, in the sense that occurred over the previous centuries, began to grow smaller.