KNOWLEDGE CIRCA 1945

Theory – To describe the shape of a wing, engineers distinguish between planform (outline of the wing viewed from above) and airfoil (shape of a fore-and-aft section). Though taking account of planform at supersonic speeds was just beginning in the mid-1940s, methods for calculating two-dimensional (i. e., planar) supersonic flow over airfoils seen as sections of a constant-chord wing of infinite span had been available for some time. The physical and mathematical principles went back to the nineteenth century, and the groundwork for aerodynamic applications had been set down in papers by Ludwig Prandtl, Theodore von Karman, and Adolf Busemann at the landmark Volta conference on “High Speed in Aviation” at Rome in 1935.3 Even at that early stage, results for the supersonic flow around a sharp-nosed airfoil could be obtained with a degree of rigor unusual for the nonlinear equations of gas dynamics.

The method has its basis in the special properties of supersonic flow. In such flows generally, a pressure signal moves past a point at the speed of sound relative to the local flow at that point. As a consequence, and in contrast to the situation in subsonic flow, a signal cannot propagate upstream, and the flow at a point on an airfoil surface cannot be affected by the shape of the airfoil aft of that point. Flow along the surface can therefore be calculated stepwise from the leading to the trailing edge, taking into consideration only the flow ahead of the point in question. With only very weak approximation, the method reduces in practice to sequential application of known nonlinear relationships for two flow situations (fig. 1): (a) discontinuous compression through a shock wave, used to find conditions at the point immediately behind the sharp concave turn at the leading edge, and (b) continuous expansion through a distributed fan-like field, to calculate flow properties along the convex surface of the airfoil. The latter relationship exists by

virtue of the simplicity of planar flow. (The Mach lines in the expansion fan of figure 1 show the limited, rearward-growing region of influence of representative points on the airfoil’s surface.) For more rapid calculation, this nonlinear “shock – expansion” method can be approximated by a linear (or first-order) theory initiated by Jacob Ackeret in 19254 or by a more accurate second-order theory put forward by Busemann in his paper at the Volta conference. By 1946, the various methods had been used to calculate the performance of a variety of airfoils.

The foregoing theories all depend on the assumption of a fictitious inviscid gas, that is, a gas lacking the viscosity present in real gases. They thus omit viscous forces and deal only with pressure forces. Such theories had long been supplemented at subsonic speeds by Prandtl’s boundary-layer theory of 1903, which deals specifically with the ffictionally retarded viscous layer that forms close to a surface in a real gas.5 On this basis, a large body of subsonic experience had been accumulated with both quantitative calculation and qualitative thinking regarding viscous effects. At supersonic speeds, little such experience was available, though indications existed that the presence of shock waves might lead to new kinds of viscous phenomena.

Experiment – Supersonic wind tunnels large enough for experiments in flight aerodynamics came into being in the 1930s. In a paper at the Volta conference, Jacob Ackeret described at length an impressive tunnel recently completed at the Federal Technical University in Zurich, and, in comments following the talk, Mario Gaspari of the University of Rome added details of a near copy then under construction at Guidonia, a short distance from Rome.6 (The most advanced tunnels, however, came into operation in 1939 at the German army’s laboratories at Peenemtlnde following small-scale development at the Technical University of Aachen. These tunnels were used in the design of ballistic missiles. Their existence did not become known in the United States until the end of World War II.)7 It was in the Guidonia tunnel that Antonio Ferri conducted in the late 1930s the first extensive experiments on airfoils at supersonic speeds. These tests, made on a constant – section model spanning the rectangular test section of the tunnel and thus simulating infinite span, supplied a wealth of pressure-distribution and other data on an assortment of airfoil shapes. Except for a few overall-force tests in the late 1920s and during World War II in small tunnels at the National Physical Laboratory in England,8 Ferri’s results provided the only experimental assessment of airfoil theory available at the time of the wing studies to be discussed here.

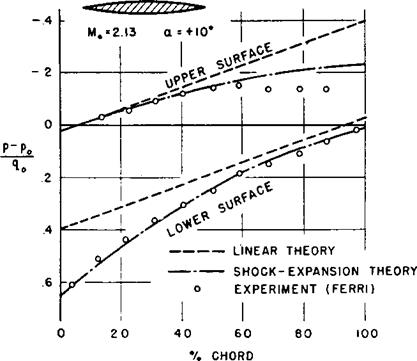
Comparison – Ferri’s findings, which were to prove useful for our Ames work, can be characterized by a figure reproduced from the latter work (fig. 2). This shows the theoretical and experimental distribution of pressure along the surface of an uncambered 10-percent-thick biconvex airfoil at a free-stream Mach number M0 of 2.13 and an angle of attack a of 10 degrees. (The Mach number M at a point in a flow is the ratio of the speed of flow to the speed of sound, both at that point.) The vertical scale in figure 2 is a dimensionless measure of the difference between the surface pressure p and the free-stream pressure p°. As is customary for airfoil work, negative values are plotted upward, positive downward, so that the area

between the upper – and lower-surface values can be seen as a close measure of the overall lift. The experimental points and the shock-expansion curve are taken from Ferri’s report; linear theory was added as part of the research to be described here.

As can be seen, Ferri’s measurements for the biconvex profile showed near agreement with the shock-expansion theory over most of the airfoil, a typical finding. The higher-than-theoretical pressures over the rear 40 percent of the upper surface he attributed to interaction between the viscous boundary later and the shock wave at the airfoil’s trailing edge. The retarded air in the boundary layer apparently lacked the kinetic energy necessary to negotiate the pressure rise through the shock wave. As revealed by optical studies, the resulting readjustment of the flow found the boundary layer separating from the surface ahead of the trailing edge, with a shock wave forming a short distance above the surface at the location of the separation and a more or less constant surface pressure from there to the trailing edge; a second shock wave formed outside the separated region at about the latter location. Because of the unpredictedly high pressures on the upper surface in the separated region, measured overall lift on the airfoil was less than calculated from the theory. Fern’s results thus brought to light one of the new viscous phenomena characteristic of supersonic flow. They also illustrate how theory and experiment are frequently used together to understand phenomena that are (a) ruled out of the theory by the assumptions that make it mathematically feasible but (b) would be difficult to comprehend without the theory for comparison. The relevance of the linear theory, which Ferri did not concern himself with, will become apparent later.