Diffusing Knowledge – The Compressor “Bible ”

One product of the NACA research program was a three-volume Confidential Re­search Memorandum, issued in 1956, often referred to as the “Compressor Bible” in the industry.32 These volumes presented a complete semi-empirical method for designing axial compressors achieving levels of performance far beyond the standard of the mid-1940s. Subsequent advances notwithstanding, including the advent of computer-based analytical techniques in the mid-1950s, this design method remained in use for at least the next quarter century, if not still today. Strikingly, however, while the “bible” often mentions turboprops and turbojets, and it expressly lays out compressor design requirements for both of them, it makes no mention of turbofans.33

The empirical component of the NACA design method was based primarily on a huge number of cascade performance tests of NACA 65-Series airfoils carried out at Langley. Airfoils in cascade perform somewhat differently from isolated airfoils. The two-dimensional wind-tunnel tests determined air deflections, irreversible pressure losses, and airfoil surface pressures as functions of incidence conditions across the family of NACA 65-Series airfoils for a range of cascade stagger angles and solidities (i. e. chord-to-space ratios). These data allowed designers first to select preferred airfoil shapes along a blade to achieve a given design performance, including thermodynamic loss requirements, and then to predict the performance of the airfoils at specified off-design operating conditions.34 In large part because of the availability of this data-base, NACA 65-Series airfoils became the most widely used airfoils in axial compressors.

Constructing a Parameter for Blade Loading – The Diffusion Factor A critical element in the NACA design method was a new parameter, devised by Seymour Lieblein and others in 1953, called the “diffusion factor.” Losses result from many effects, but most important, in the absence of shocks, are viscous losses related to diffusion – i. e., deceleration – acting on boundary layers. As the loading on a given airfoil increases, a point is reached where the losses abruptly increase. Designers needed a non-dimensional parameter that could serve as a measure of the loading, allowing them to anticipate, in the form of a critical value, where the losses abruptly increase. Axial compressor blading had originally been conceptualized on the basis of isolated airfoil theory, using the lift coefficient as a non-dimensionalized measure of loading, but the losses in cascades did not correlate well with it. As a consequence designers did not have an adequate way of anticipating loading limits. Other parameters were tried before the diffusion factor, but with limited success.35

The diffusion factor was derived from a series of simplifying assumptions from boundary layer theory, applied to the suction surface. The basic idea was that the ultimately dominating losses came from turbulence developing in the boundary layer along the rear half of the airfoil suction surface, where the velocity drops from its peak to its discharge value. The problem was that any correlating parameter had to be defined in terms of quantities that could be determined with confidence; this did not include the peak velocity along the suction surface in rotating blade rows. The simplifying assumptions allowed this peak velocity to be replaced by quantities that could be measured upstream and downstream of blade rows:

W2 ^2C02“rlC01

0=1 2 rm<5Wx

where W is the relative velocity, C0 is the absolute tangential velocity, о is the cascade solidity, the subscripts 1 and 2 designate upstream and downstream of the blade row, and rm is the average of the radii rj and r2. The multi-term structure of this formula should make clear that Lieblein’s diffusion factor was not an entirely obvious, intuitive parameter. Yet, when assessed against the NACA 65-Series cascade data, it turned out to indicate a clear loading limit criterion.36 This criterion was equally successful when tried with cascade data from other airfoils.37 It has subsequently proved to be applicable to compressor blading quite generally, lending an element of rationality to compressor design much as the lift coefficient did to wing design.38

The importance of having a clear loading limit criterion is best seen by considering the ramifications of not having one. The obvious way to pursue improvements in performance was by trying to develop new airfoils; and the natural way of trying this was to test airfoils in cascade and then make incremental modifications in shape that promised incremental gains in performance. The problem with this approach in the absence of a clear loading limit criterion was that any incremental modification in shape might well cross some unrecognized barrier, resulting not in an incremental gain, but in a prohibitively large fall-off in performance. The diffusion factor and the empirically determined loading limit expressed in terms of it defined the barrier that the exploration of new airfoil designs needed to remain within.

The diffusion factor did indeed play a key role in the pursuit of higher stage pressure-ratios. The overall pressure-ratio of a compressor amounts to a product of the individual stage pressure-ratios. The pressure-ratio per stage tends to increase as the velocity of the flow relative to the rotating blades increases. As the so-called velocity triangles shown in Figure 6 indicate, if the flow approaching a rotor blade

is axial in the absolute frame of reference, then the velocity relative to the rotor blade increases as the blade tip-speed increases. Ultimately, stress considerations limit tip-speed. Aerodynamic considerations, however, were imposing limits on tip – speed far below those imposed by stresses. As the relative incident Mach number at the tip increases, shocks begin to form in the outer portion of the airfoil passages, resulting in a sharp increase in losses. In the case of NACA 65-Series airfoils, the ‘ losses rise sharply for incident Mach numbers above 0.8. This limited the pressure – ratio in stages using these airfoils to around 1.15, as we saw earlier.

Pushing Blade Loading – Transonic Stages This restriction, coupled with the goals of achieving higher pressure-ratios per stage in order to use fewer stages, hence saving weight, and higher airflow per unit frontal-area, hence limiting engine drag, led to the research problem of finding airfoil shapes that would allow the incident tip Mach number to rise above 1. That is, the goal was to find airfoil shapes that would permit efficient transonic stages – stages in which the inlet relative velocity is supersonic in the outer portion of the blade and subsonic in the inner portion (which, at the same RPM, is moving at a lower velocity). NACA researchers at Langley and Lewis had been working on the problem of transonic airfoil and stage design from 1947 on as another part of their axial compressor research program. They had achieved some successes before the diffusion factor was identified – e. g. a stage with a 1.1 tip Mach number without excessive losses39 – but not consistently. They began having more success with the diffusion factor in hand by limiting attention to velocity triangles that met the loading limit criterion for this parameter. In particular, they designed an experimental 5-stage transonic compressor with a tip-speed of 1100 ft/sec in which the tip Mach numbers were as high as 1.18. Although the efficiency fell off at 100 percent speed, this compressor did achieve an overall pressure-ratio of 4.6 at an adiabatic efficiency of 85 percent, or, in other words, an average stage pressure-ratio of 1.3 5.40 Furthermore, the measured performance of the double-circular-arc airfoils used in these and other NACA test stages, along with wind-tunnel testing of double­circular-arc cascades, began to yield a data-base for transonic airfoils, supplementing the NACA-65 Series data-base.

Save perhaps for the early efforts in the mid-1940s, the NACA work on transonic stages was focused on improving axial compressors, not on fans that could be used in bypass engines. The primary application of the NACA transonic stage research was in the early stages of axial compressors, yielding both higher pressure-ratio per stage and higher airflow per unit frontal-area.41 Nevertheless, as we shall see, NACA’s success in pushing tip Mach numbers well above 1.0 was an important step in the emergence of the turbofan engine. Turbofans with tip Mach numbers below 1 would have offered at most only small gains in performance over turbojets. Once it became clear that the tip Mach number can exceed 1.0 without a large drop­off in performance, the question became, how far above Mach 1 can the tip Mach number go?

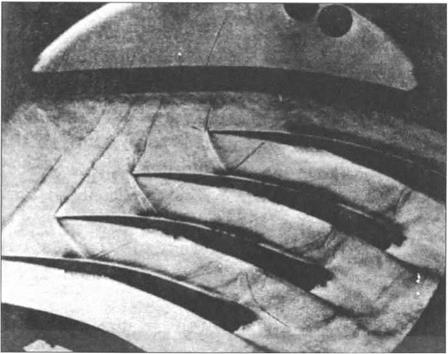
Pursuing a Quantum Jump – Supersonic Stages Another, more radical part of the NACA compressor program proved in hindsight to be even more important to the emergence of the turbofan engine. It explored a some­what revolutionary way of trying to achieve higher pressure-ratio per stage: actually using the sharp pressure increase across a normal shock to greatly increase the pressure rise in a stage. The idea of a supersonic compressor stage – one in which the incident relative velocity is supersonic along the entire span of the blade – was first proposed in 1937. Arthur Kantrowitz initiated research on supersonic stages at NACA Langley in 1942. Shortly after the War several young engineers joined him, forming a research group at Langley and then at Lewis as well. Their fundamental problem was to control and limit the thermodynamic losses in a supersonic stage. The abrupt pressure-rise across the shock acts as an adverse pressure-gradient at the point where it meets the boundary layer, threatening to cause the boundary layer to separate, resulting in large losses. An example of such shock-induced boundary layer separation is shown in Figure 8, for a Mach number of 1.5. The problem was to find

Figure 8. Shock waves and boundary layer separation in a Mach 1.5 cascade. Note shock waves at blade tips (left). Boundary layer separates on suction (i. e. convex) surface, where the shock intersects it (dark region above each airfoil), with attendent thermodynamic losses. [F. A.E. Breugelmans, “High Speed Cascade Testing and its Application to Axil Flow Supersonic Compressors,” ASME paper 68-GT-10, 1968, p. 6.]

airfoil shapes for which the attendant losses would be greatly outweighed by performance gains. Since analytical methods at the time were worthless for attacking this problem, the only approach was to learn through testing experimental designs.

NACA engineers designed and tested an impressively large number of experimental supersonic stages between 1946 and 1956.42 Virtually all of these research compressors performed poorly when judged by the standards that would have to be met for flight. In the last years of the effort, however, some designs began showing promise. Of particular note was a 1400 fit/sec tip-speed compressor rotor designed by John Klapproth and others, which took into account Lieblein’s diffusion factor. It achieved a pressure-ratio of 2.17 at an adiabatic efficiency (for the rotor alone) of 89 percent, with a tip Mach number of 1.35. As the report describing these results notes, however, its greatest significance lay elsewhere:

Inlet relative Mach numbers were supersonic across the entire blade span for speeds of 90 percent design and above. There were no appreciable effects of Mach number on blade-element losses below 90 percent of design speed. At 90 percent design speed and above, there was an increase in the relative total – pressure losses at the tip. However, based on rotor diffusion factor, these losses for Mach numbers up to 1.35 are comparable with the losses in subsonic and transonic compressors at equivalent values of blade loading.43

This was the first clear evidence that losses continue to correlate with the diffusion factor to much higher Mach numbers than in the tests which had provided the basis for this parameter – a result that was by no means assured a priori.

…. While the derivation of the diffusion factor D was based on incompressible flow, the primary factors influencing performance, that is, over-all diffusion and blade circulation, would not be expected to change for high Mach number applications…. The applicability of the correlation of D should be expected only in cases having similar velocity profiles on the blade suction surface. This similarity existed for the theoretical velocity profiles for this rotor, although the actual distribution was probably altered somewhat by differences between the assumed and real flow. On the basis of [our results], the diffusion factor appears to be a satisfactory loading criterion even for very high Mach number blading when the velocity distribution approximates that of conventional airfoils in cascade 44

In other words, for the first time, the performance in a supersonic blade row cor­related continuously – i. e. seamlessly – with the performance achieved in subsonic and transonic compressor stages, up to as high as Mach 1.35. An approach to design­ing much higher Mach number stages was beginning to emerge.45