Negotiating Kelvin’s Theorem
Prandtl’s lecture had the title “The Generation of Vortices in Fluids of Small Viscosity.” The choice of subject matter is revealing. Prandtl used the opportunity to address the two problems that most worried the British. First, how did circulation arise? Second, why did perfect fluid theory, though false, work in practice? Prandtl argued that these problems can be resolved by a careful analysis of what is, and what is not, implied by the theorems of classical hydrodynamics.
Consider Kelvin’s theorem, which, in Prandtl’s words, asserted that “in a homogeneous, frictionless fluid the circulation around every closed fluid line is invariable with time.” What did Prandtl mean by a “fluid line”? A closed fluid line is not just a closed geometrical line imaginatively and arbitrarily projected into the fluid. It is meant to be a line that is always made up of the same fluid elements. “Let us suppose a ‘fluid line’ to be a line composed permanently of the same fluid particles” (722). If the whole of a body of fluid is at rest, then the circulation around any such circuit is zero, and it follows from Kelvin’s result that it will stay zero for all time. Prandtl then invited his listeners to imagine a body, such as a wing or strut, surrounded by perfect
|
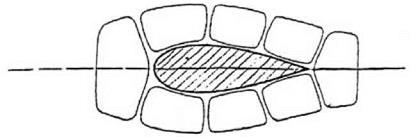
figure 9.13. Stationary fluid around a strut subdivided into a mesh of fluid lines. From Prandtl 1927c, 723. (By permission of the Royal Aeronautical Society Library) |
fluid where the fluid is at rest. The fluid around the object is supposed to be subdivided into a mesh of small circuits in the manner shown in figure 9.13, where each circuit is a fluid line.
Kelvin’s theorem implies that the circulation around each circuit or fluid line remains zero, and this apparently leads to the conclusion that rotation cannot appear anywhere. From this it would seem to follow that lift is precluded, as the British critics of the circulation theory always argued. For Prandtl, however, “this conclusion is premature” (722). He went on: “We must first ascertain whether every point of the fluid set in motion is actually enclosed by the lines which in the state of rest were closed, if our conclusion is to be permissible. But closer investigation shows that it is possible to give instances in which this is not the case” (722).
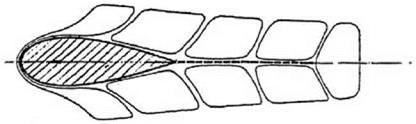
How is this possible? Where do the rotating fluid elements come from? Prandtl’s answer was based on what happens when the body moves through the fluid “so that the upper and lower streams flow together, or as we shall say become confluent, at the sharp rear edge of the body” (723). Such a motion is shown in figure 9.14.
The network of circuits is divided by a surface “along which our conclusion as to the absence of vorticity is no longer applicable” (723). This surface is indicated by the dotted line in the figure. The vorticity does not arise because some material element of fluid is set in rotation; it comes from the relative motion of two adjacent bodies of fluid. Prandtl did not try to challenge Kelvin’s theorem by finding a drop of perfect fluid that somehow escaped the division into closed circuits; rather, he was exploiting the fact that rotation (defined technically) can exist without anything (or any finite thing) rotating. Kelvin’s theorem does not imply that “rotation cannot appear anywhere”; it has a more specific, and limited, meaning. A vortex sheet, Prandtl insisted, can arise from confluence, and do so “without contradicting Kelvin’s theorem” (723).
|
figure 9.14. Strut in motion with confluence at rear edge. Prandtl argued that circulation can be created in an ideal fluid by confluence without violating Kelvin’s theorem. From Prandtl 1927c, 723. (By permission of the Royal Aeronautical Society Library) |
Confluence, according to Prandtl, can also generate the circulation around a wing. In an attempt to show how it can do this, he set out the sequence of events in the first few moments after a wing has begun to move through still air. Prandtl referred to the lower surface of the wing as the “pressure” side and the upper surface as the “suction” side. “During accelerations,” he said,
the velocity at the rear edge is greater on the pressure side than on the suction side, since the path along the pressure side is shorter. Consequently, after confluence a discontinuous distribution of velocity is set up which effectively constitutes a sheet of intense vorticity; the surface of discontinuity then begins to roll up into a spiral. The circulation for each circuit enclosing the wing and the surface of discontinuity still remain zero, from which it may be inferred that the circulation around the wing is equal and opposite to the circulation of the vortex produced by rolling up of the sheet. This is the method of generation of the circulation around the wing. (723)
It cannot be said that the argument is entirely clear.70 Prandtl acknowledged that “the mathematician” would object and insist that an inviscid fluid would flow around the trailing edge. There would be a stagnation point on the upper (suction) surface of the wing rather than a vortex sheet coming away from the trailing edge. This would be so even if the trailing edge were sharp and the perfect fluid had to move at an infinite speed to get round the corner. The result would be no circulation and no lift. This must be the correct flow, the mathematicians would say, because it would be “everywhere irrotational in accord with the theoretical laws for a flow produced from a state of rest!” (723). For the mathematicians, this flow alone would be consistent with the theorems of Lagrange and Kelvin. On Prandtl’s reading the theorems do not carry this implication. He argued that both his proposed flow (with circulation) and the mathematician’s flow (without circulation) were consistent with the classical theorems of hydrodynamics. But, he insisted, only the flow with circulation and the smooth confluence at the trailing edge is physically realizable. This was really all Prandtl needed. Even if the process by which circulation was generated remained obscure, it was the logical possibility of circulation, and the logical right to postulate it, that really mattered for the perfect fluid approach.
Prandtl then turned to his second topic: Why did perfect fluid theory work? Going back to his discovery of the boundary layer in 1904, he explained that the thickness of the layer was inversely proportional to the square root of the viscosity and that it generated a tangential friction proportional to the 3/2 power of the speed and the square root of the viscosity. “But,” he said, “there is something of more importance to us here” (725). The boundary layer is the cause of the formation of vortices. Kelvin’s theorem only applies to flows devoid of viscous forces, and so, in motion starting from rest, the circulation will remain practically zero in fluid circuits that do not pass, or have not passed, through a boundary layer. This is why real fluids, such as air, behave like perfect fluids in irrotational motion at a distance from a solid body. By means of photographs and a film Prandtl then demonstrated that the boundary layer could be manipulated, for example, removed by suction, and he showed that this procedure had a dramatic effect on the flow. He concluded his lecture with a discussion of the role of turbulence in the boundary layer and explained that an increase in turbulence could reduce drag. This allowed Prandtl to clinch his justification for using perfect fluid theory: “We thus get the unique characteristic that it is precisely these turbulent flows of low resistance around bodies which can be so closely represented by the theory of the perfect liquid” (739).
No one could say that Prandtl had evaded the arguments of his British critics. He had confronted their doubts, but had he dispelled them? The utility of Prandtl’s wing theory had been largely conceded, but did the Wright Lecture remove the residual worries about its theoretical basis? The immediate answer was that it did not. Partly this may have been because of the difficulty in following certain steps in Prandtl’s line of thought, but a deeper reason lay in the divergent readings of Kelvin’s theorem.