The Horseshoe Vortex and the Biot-Savart Law
Prandtl’s earliest publications on aeronautics did not deal with the circulation theory of lift in either its two – or three-dimensional form. He wrote mainly on airships, the general mechanical problems associated with building an airplane, or the engineering that went into the construction of wind channels for testing models. Thus in June 1909 he lectured to the annual general meeting of the association of German engineers at Mainz on the significance of the model experiments to be done at Gottingen and the equipment that had been developed.47 September of the same year saw him speaking at the International Aeronautical Exhibition (ILA) in Frankfurt. Here Prandtl concentrated on the principles and preconditions of flight and the practical problems of achieving adequate lift and stability.48 In a series of articles in the new Zeitschrift fur Flugtechnik he laid out for the reader’s benefit those parts of mechanics of special relevance to aeronautics.49 His topics included gyroscopes, stability, and air resistance, with a mention of his own boundary – layer theory in connection with the phenomenon of separation and vortex formation. One of Prandtl’s concerns was to remove false ideas that continued to cause trouble in the field. Many “inventors,” he explained, tried to achieve automatic stability in aircraft by some sort of pendulum device whose rationale was based on a misunderstanding. Prandtl also stressed that resistance depends as much on the suction effects behind a body as it does on what happens at its front face. From the outset he had no time for Rayleigh – Kirchhoff flow as an account of lift. He viewed it as wrong at the level of general principle.
In these articles for the ZFM, Prandtl recommended some of the relevant literature (64). Significantly he included both Lanchester’s book on aerodynamics and Lamb’s book on hydrodynamics. He thus symbolically conjoined what, in the homeland of those two authors, was proving so resistant to unification. On the first page of the initial article in the ZFM series, Prandtl also nailed his colors to the mast regarding the principle of the unity of theory and practice. Not for him the slogans of the antimathematical movement, which treated theory, and especially mathematically based theory, as something in fundamental opposition to practice. Using words that closely echoed the for
mulations adopted a decade earlier by August Foppl, in the preface to his Vorlesungen uber technische Mechanik, 50 Prandtl asserted:
Um nun meine Absichten naher zu kennzeichnen, mochte ich vorweg be – tonen, dafi ich das viel ausgesprochene Schlagwort vom Gegensatz zwischen Theorie und Praxis nicht gelten lassen will; der Gegensatz liegt fur mein Emp – finden zwischen guter und schlechter, richtig und unrichtig angewandter Theorie; eine gute Theorie is in Ubereinstimmung mit den Ergebnissen der praktischen Erfahrung, oder sie gibt zum mindesten wesentliche Zuge der Er – fahrungstatsachen wieder. (3)
In order to characterize my intentions more precisely, I should emphasize at the outset that I do not want to endorse the much used slogans about the opposition of theory and practice. In my experience the contrast lies between theories that are good or bad for application and between correctly or incorrectly applied theories. A good theory is in agreement with the results of practical experience or, at least, captures the essential thrust of the facts of experience.
Prandtl was not just striking attitudes. His work on the three-dimensional wing would meet the demanding requirement of applicability to engineering practice.
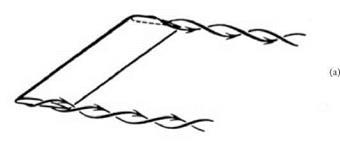
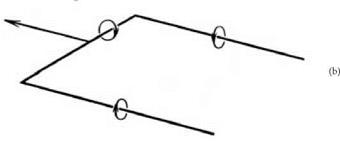
Prandtl tells us that it was in the winter semester of 1910-11 that he began to develop his own mathematical theory of the finite wing.51 It was treated in a course of lectures that he gave in Gottingen on the theme of aeronautics. The lectures were attended by Otto Foppl and, though the text of the lectures appears to have been lost, hints and mentions of their content are to be found in the early papers coming from the Gottingen group. The basic picture with which Prandtl worked was similar to the one already proposed by Lanchester, namely, a finite wing with circulation around it and with two vortices emerging from the wingtips. Prandtl’s aim was to make this picture amenable to a mathematical analysis, but to do so he had to resort to extreme simplification. He treated this complex three-dimensional, physical system as equivalent to three connected-line vortices. One vortex, called the bound vortex, represented the wing and was assumed to run along the span of the wing. The other two vortices, called free vortices or trailing vortices, extended back from the wingtips and were at right angles to the wing. The arrangement, as shown in figure 7.5, first appeared in a brief, qualitative account of the theory that Prandtl published in 1912.52 The two diagrams, which show the progressive abstraction of the picture, reappeared in Prandtl’s published lectures in the form shown here.
Physically the trailing vortices are assumed to extend right back from the wing in flight to the point where the aircraft left the ground. Mathematically
|
|
|
figure 7.5. Trailing vortices from the wingtips represented diagrammatically (a) and by the even more simplified “horseshoe” vortex system (b). Tietjens 1931, 197. (By permission of Springer Science and Business Media) |
they are said to extend back “to infinity.” The three connected vortices thus form a single bent line of vorticity. A vortex line in an ideal fluid (whether straight or bent) has the same strength everywhere along its length, so the circulation Г around the wing, that is, around the bound vortex, also gives the vortex strength along the trailing vortices. For reasons examined later, this model was called, rather implausibly, the Hufeisen Schema, or “horseshoe schema.”
Prandtl’s task was to see how the presence of the two trailing vortices modified the flow in the vicinity of the wing. If the trailing vortices are ignored (as they are in the two-dimensional case), the law of lift is (using the usual notation) Lift = p V Г. Is this law preserved in the three-dimensional case? Surely some significant modification of the flow must occur, and this must have some consequences for the behavior of the wing—but what modifications and what consequences? Before I go into mathematical details, it may be useful to sketch the outcome of Prandtl’s analysis in qualitative terms. Using his simplified model, Prandtl was able to predict two unexpected and important effects.
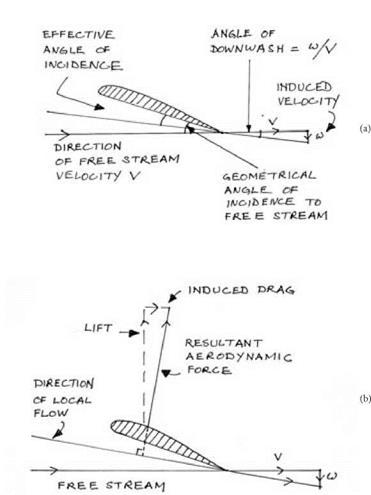
First, Prandtl found that the effect of the trailing vortices ought to be the creation of a downwash at, and behind, the wing. The swirling air of the trailing vortices would (according to his mathematical analysis) influence the air in the vicinity of the wing in such a way as to give it a downward velocity component. The downward component would have the effect of tilting the airflow. The way that the tilt arises from the introduction of the downwash component is shown in figure 7.6a. The presence of the tilt means that the wing operates at a slightly lower angle of incidence relative to this new local flow. The effective angle of incidence is therefore reduced. Because (over the working range of the aerofoil) lift is proportional to the angle of incidence, the lift should be reduced. The same point may be expressed the other way round. In order to get the same lift per unit length in a finite aerofoil as in an infinite aerofoil of the same cross section, the angle of incidence relative to the main flow has to be increased.
The second prediction followed from the first. If the resultant lift force on the wing is at right angles to the local flow, and the local flow is tilted in the manner shown in figure 7.6b, then the resultant aerodynamic force will be tilted back relative to the main flow and hence to the direction of motion of the wing. The effect will be that the resultant force will now have a component that opposes the motion. There will be a drag. It is important to recall that this analysis was all done using ideal-fluid theory. The two-dimensional analysis showed how a flow involving a vortex and circulation could yield a lift but no drag, the three-dimensional analysis now predicts that it can produce both a lift and a drag. For reasons that will become clear in a moment, Prandtl and his co-workers came to call this novel drag an “induced drag,” and the tilt of the local flow due to the downwash was called the “induced angle of incidence.” Induced drag was a form of drag that did not result from viscosity or skin friction or turbulence. It was produced by the very same inviscid mechanisms that generated the lift.
Having sketched these two initial predictions, I now look at their mathematical derivation. How did the idealization of the “horseshoe” vortex help Prandtl to develop a mathematical description of the flow which led to these results? The answer lies in an analogy that exists between the hydrodynamics of a perfect fluid and electromagnetic phenomena. A line vortex is like a wire carrying an electric current which sets up, or “induces,” a magnetic field around it. The vortex in an ideal fluid does not, of course, induce a magnetic field, it induces a velocity field. The velocity was exactly what Prandtl wanted to understand because once he had a mathematical expression for the velocities, he could deduce the pressures, and thus the forces on the wing. Prandtl’s use of the analogy was explicit. “Fur die Verteilung der Geschwindig – keit in der Umgebung irgendeines Wirbelgebildes besteht eine vollkommne
|
|
figure 7.6. In (a), the trailing vortices induce a downward component win the flow behind the wing. This tilts the airflow and effectively lowers the angle of incidence of the wing. The new “effective” angle of incidence is the original geometrical angle of the wing to the free stream minus the angle of the downwash produced by the tailing vortices. In (b), the tilt in the airflow means that the resultant aerodynamic force, which is at right angles to the local flow, is no longer at right angles to the free stream, that is, the direction of motion. This produces a drag component called the “induced drag.”
Analogie mit dem Magnetfeld eines stromdurchflossenen Leiters”53 (For the velocity distribution in the neighborhood of any such vortex formation there exists a complete analogy with the magnetic field around a current carrying conductor).
The analogy to which Prandtl referred was well known before the work on
aerodynamics and was discussed in standard textbooks in both electromagnetic theory and hydrodynamics. It was to be found in the books on Maxwell’s theory and on technical mechanics written by Prandtl’s own teacher and father-in-law, August Foppl.54 The analogy is not a superficial one but exists at the level of the fundamental equations that can be used to describe the two different areas. Experts in electromagnetism, such as August Foppl, could easily describe the magnetic effects of a current-carrying wire shaped in the form of the idealized “horseshoe,” and Prandtl carried these results over to the corresponding system of line vortices.
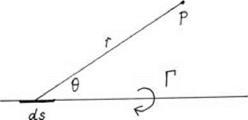
The law of induction common to the hydrodynamic and electromagnetic cases is called the Biot-Savart law.55 The law may be explained by considering figure 7.7, which shows an infinite, straight-line vortex of strength Г. A small segment of the vortex is identified as ds. The point P lies at a distance r from the vortex element, and the line joining ds and P makes an angle 0 (theta) with the vortex. Following the electromagnetic analogy, there is a small component of velocity dw “induced” at the point P by the small element ds. According to the Biot-Savart law, the component is
, rds. sind
dw = -—.
4nr
The velocity component is perpendicular to the plane determined by ds and the line r. This formula links infinitesimal quantities, and the causal relation between such infinitesimals that seems to be implied by the law occasioned some puzzlement. August Foppl had no time for such subtleties. Taken by itself, said Foppl, the formula has absolutely no meaning: “Es hat uberhaupt keinen Sinn.”56 Foppl’s point was that the real significance of the law only
|
figure 7.7. According to the Biot-Savart law, the infinitesimal amount of induced velocity dw at a point P due to the infinitesimal vortex element ds of a vortex of strength Г is given by the formula dw = (Г/4ТСГ2) ds sin0. |
emerges when it is integrated in order to give the finite effect of a finite length of vortex or, by extrapolation, the finite effect of a very long (and effectively infinite) vortex. This is what Prandtl needed in order to compute the effect of the, effectively infinite, trailing vortices.
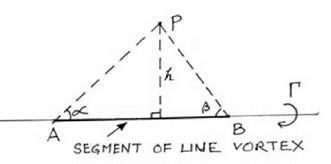
As Prandtl first employed it, the Biot-Savart law was used to give the finite velocity component w at an arbitrary point P in the vicinity of a finite, straight-line segment AB of a vortex (see fig. 7.8). If the strength of the vortex is Г, and the point P is at a perpendicular distance h from the line AB, then, after integration, the law now reveals that the contribution to the velocity of the finite segment is
Г
w = (cosa + cos в).
4nh
The angles a and в are the angles made by the lines joining the point P with the ends of the finite vortex segment under consideration. The direction of the velocity w at P is at right angles to the plane that passes through the points A, P, and B. Whether the velocity vector faces downward, into the page, or upward, depends on the sense of the circulation around AB. (If an observer who looks from B to A is confronted with a clockwise circulation, then the induced velocity vector points into the page and vice versa.) Notice that if the finite line segment AB is extended to infinity in both directions (so the angles a and в get smaller and smaller as the line gets bigger and bigger), then the velocity at point P should correspond to the velocity at a point situated a distance h from the center of a two-dimensional vortex, that is, a point vortex, of circulation Г. This is exactly what the formula provides. The expression (cos a + cos в) assumes the value 2 for a = в = 0, so that w = r/2nh.
|
figure 7.8. The induced velocity w at a point P due to a finite vortex segment AB of a vortex of strength Г is, according to the Biot-Savart law, w = (Г/4-nh) (cosa + cosp). |
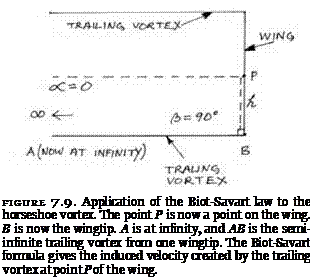
Prandtl’s aim was to apply the Biot-Savart law to the “horseshoe” vortex because he was interested in the effect of the trailing vortices. The trailing vortices count as “semi-infinite” lines because they start from the wingtip and go to infinity in one direction. To understand Prandtl’s reasoning when he applied the law to his horseshoe system, think of the arrangement in figure 7.8 modified in two ways until it turns into that in figure 7.9. First, A is moved to infinity so that a = 0 and cos a = 1. Second, the point B is moved inward until it coincides with the base of the perpendicular from P. This makes в = 90° so that cosP = 0. The formula then gives the value for the induced velocity w:
Г
w = .
4nh
Interpreted in terms of the horseshoe vortex model of the wing, this formula gives the contribution of one of the trailing vortices to the flow at a point on the wing that is distance h from the wingtip generating the vortex. The full downwash at any given point on the wing needs the contribution of both trailing vortices to be added together, but the formula reveals the mechanics of the process that generates the downwash. Prandtl spoke of a zusatzliche Abwartsgeschwindigkeit, an additional downward speed. Max Munk called the quantity w the “induced velocity,” and this name was taken over by the Prandtl school.
 |
Sufficient has now been said to show how Prandtl was able to reach his predictions about the general effect of the trailing vortices, that is, (1) the
creation of a downwash, (2) the tilt that the downwash creates in the local flow, and (3) the resulting (induced) drag. One final point to notice about the formula for the induced velocity w of the downwash is that it takes the form of a fraction with h in the denominator. It contains a singularity at the point h = 0. For this value of h, the formula requires that the velocity w be infinite, which is physically impossible. Recall that h refers to the distance from the wingtip. This means the application of the Biot-Savart law to the horseshoe model of the three-dimensional wing breaks down for points close to the wingtip. Prandtl had made novel and important predictions, but, because of the singularity, the predictions carried with them a problem. Even if in many cases they were proven correct, they were based on a physically impossible model.