Generalizing the Mathematics

Not only is a perfect fluid a theoretical substitute for a real fluid, but the geometry of the Joukowsky profile is a theoretical substitute for a real aero­foil section. The mathematics of the Joukowsky transformation of a circle always gives a profile with some highly unrealistic properties. At the trailing edge, the tangents to the upper and lower surfaces of the wing coincide with one another. The trailing edge is like an infinitely thin blade. No engineer would design such a wing, and no workshop could produce one. At most they could produce an approximation of the kind that the Gottingen workshops must have produced for Betz. This raised a question: Could the mathemati­cal advantages of the Joukowsky transformation be retained while avoiding the unrealizable features of the profile? Could a transformation be found that turned a circle into a winglike profile whose trailing edge met at some speci­fied, nonzero, angle? The answer to these questions is yes.

Once again it was members of the technische Hochschule at Aachen who provided the answers. In 1918 Theodore von Karman and Erich Trefftz showed that this job could be done by a transformation from a circle in the Z-plane to a wing profile in the z-plane that took the form

z – kl _ (Z-l)k z + kl ~ (Z + l)k ’

where k is a constant less than 2 and l is the length that featured in the pre­vious discussions by Blumenthal. Whereas the Joukowsky transformation effectively draws a wing profile that has a circular arc as “skeleton,” the

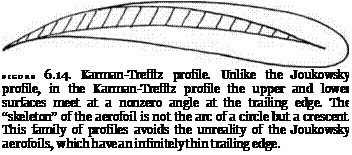Karman-Trefftz transformation produces an aerofoil that has a crescent or sickle shape, made up of two circular arcs, as its “skeleton.”61 Just as the trail­ing edge of the Joukowsky profile shades into, and becomes, the single arc of its skeleton, the Kutta arc, so the trailing edge of the new profile combines with, and becomes, the endpoint of the crescent (see fig. 6.14).

Von Mises pointed out that the Karman-Trefftz formula is a close relative of the Joukowsky formula.62 Starting with a Joukowsky transformation in the form

he showed the link in three simple steps. First, subtract the quantity 2І from both sides. Second, write down the Joukowsky formula again and, this time, add 2І to both sides. Third, form the quotient of these two expressions. The result is another version of the Joukowsky transformation that looks like this:

z – 2l = (Z-1 )2 z + 2l _ (Z +1)2′

The Joukowsky transformation, with its knife-blade trailing edge, is thus a special case of the Karman-Trefftz transformation, that is, the case where the exponent is k = 2. Replacing the exponent 2 by a value of k where k < 2, gives the formula for a transformation that generates an aerofoil with a more real­istic trailing edge. As k gets smaller, the angle at the trailing edge gets larger.

Von Karman and Trefftz ended their paper by posing the following ques­tion: Given some arbitrary, but plausible, aerofoil shape, is it possible to dis­cover a transformation that will relate it to a circle and thus allow the flow to be predicted? It is one thing to be given, or to discover, a transformation that will go from a circle to an aerofoil-like shape, but starting with an aerofoil and trying to find the transformation is quite a different matter. This is the

question that an aircraft designer would pose. What will be the properties of the wing if it is built like this rather than like that?

Von Karman and Trefftz argued that if a conformal transformation is applied in reverse to some given profile, it may not turn it back into a circle but will turn it into a shape that is not greatly removed from a circle. They then offered a transformation that would, to an adequate degree of accuracy, turn this near circle into a better circle. They thus began to address the way in which ideal-fluid theory could be applied not just to a few favored “theoreti­cal” aerofoils, but to any shape that might come from the drawing board of a designer—shapes that would be strongly influenced by the contingencies of the construction process.

The Karman-Trefftz transformation showed how to avoid the unrealistic cusp at the trailing edge of the Joukowsky profile, but it did this at the price of a certain complexity. Betz argued that the extraordinary simplicity of the orig­inal Joukowsky transformation was worth preserving. The Karman-Trefftz transformation, he said, was difficult to use in practice. He then exhibited a much simpler way to achieve a finite angle at the trailing edge by a modi­fication of the original graphical method used by Blumenthal and Trefftz. The modification produced a profile with a slightly rounded rear edge, and this again raised the problem of the position of the rear stagnation point. How was the circulation to be determined? Betz declared that from a practi­cal point of view this indeterminacy was of no great significance because the real circulation was always smaller than the theoretical prediction. In reality, even the usual Joukowsky profiles do not unambiguously determine the cir­culation: “also auch bei gewohnlichen Schukowsky Profilen nicht eindeutig bestimmt ist.”63 Betz suggested that some point on the rounded edge could be designated to play the role of the sharp edge of the original profile when calculating the circulation.

The cusp on the trailing edge of the Joukowsky profile was not the only problem. There were other respects in which this family of aerofoil shapes differed from those which experience and practice were beginning to favor. Typically, Joukowsky profiles were too rounded and bulky at the front and too thin at the back, even when the zero angle of the trailing edge was avoided. Also, the maximum camber lies near the center of the chord rather than, as was preferred in practice, in the first third of the chord. How were these prob­lems addressed? In a series of articles in the Zeitschrift fur Flugtechnik, begin­ning in 1917, Richard von Mises suggested a generalization of the Joukowsky transformation that could yield aerofoils that met almost any specifications of their geometrical properties. Such aerofoils could be designed in a way that

avoided the faults identified in the original Joukowsky profiles.64 Von Mises explored transformations of the following kind:

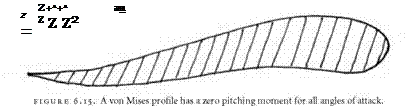
Any aerofoil could be described given a sufficient number of terms in this sequence.65 The Joukowsky transformation was a special case of the formula for which n = l. Von Mises also wanted to show how the parameters that governed the conformal transformation of the circle were related to the aero­dynamic characteristics of the resulting wing. For example, he showed how to construct a profile in which the resultant aerodynamic force always acts through the same point of the wing, a point that came to be called the aero­dynamic center of the wing. The result was that the pitching moment of the wing was zero for all moderate angles of attack (that is, for the straight-line part of the curve relating lift to angle of attack). This was a property of poten­tial importance for the stability and handling properties of an aircraft. The general shape of a von Mises profile is shown in figure 6.15. Like the Karman – Trefftz profiles, it avoids the cusp at the trailing edge, but in addition it is characterized by a shallow S-shape with a slight upturn at the rear edge.