Betz on Pressure Distributions

Knowing the predicted pressure distribution along a specified aerofoil opens up the possibility of subjecting the circulation theory of lift to a demand­ing empirical test. Does the predicted distribution correspond to the real

figure 6.io. Ludwig Prandtl (left) and Albert Betz (right) standing in front of one of the Gottingen wind tunnels. In the early years of aerodynamics, Betz was second only to Prandtl in the scope of his theoretical and experimental investigations. (By permission of Zentrales Archiv, Deutsche Zentrum fur Luft und Raumfahrt)

distribution in as far as it can be measured? In 1915, two years after Blumen – thal’s theoretical analysis, a detailed experimental study was published in the Zeitschrift fur Flugtechnik that was designed to answer this question. The pa­per was by Albert Betz, Prandtl’s close collaborator in Gottingen (fig. 6.10). It was called “Untersuchung einer Schukowskyschen Tragflache” (An investiga­tion of a Joukowsky wing).60

Betz used one of Blumenthal’s profiles and worked with a model wing that had a span of 50 cm and a chord of 20 cm. It had a curvature (f/l) of 1/10 and a thickness ration (8/l) of 1/20 and so corresponded exactly to the second of the four profiles described by Blumenthal (that is, the one shown in fig. 6.9). Betz’s aim was to use wind-tunnel data to test Blumenthal’s predicted lift and pressure distribution.

The model wing-section was manufactured from metal plate in the form of an airtight, hollow body and made to conform as precisely as possible to the theoretical, Joukowsky profile. Following Fuhrmann’s work on model airships, the wing was fitted with bore holes and the hollow interior was connected by a thin pipe leading from the wingtip to a manometer. This enabled pressure measurements to be taken at a number of points on the surface along the chord of the wing. Measurements were taken with one hole at a time exposed while the other holes were smoothly plugged. The line of bore holes was not positioned at the center of the span but was displaced a few centimeters to one side. This was to avoid interference to the flow of air over the holes from the strut that had to be attached to the wing in order to hold it rigidly in place in the wind tunnel. As well as the pressure, Betz also needed to know the overall lift and drag of the wing. For this the wing had to be suspended on a balance so that force measurements could be made. Dur­ing this phase of the experiment, the pipes leading to the manometer were disconnected and all the bore holes plugged.

It was necessary to make sure that the experimental arrangement pro­vided a good approximation to the infinite wing presupposed in the math­ematics. Joukowsky had simply made his wing section run from the top to the bottom of the shallow Moscow wind tunnel. This is the basis of all attempts to realize a two-dimensional flow, but Betz put a lot of effort into refining the technique. His aim was to make the test section as free as possible from disturbing effects produced by the walls of the tunnel and the join between the walls and the ends of the wing. An elaborate system of auxiliary sidewalls, gaskets, and seals was designed and tested to ensure a uniform flow across the experimental cross section of the wing. Once he had an acceptable approxi­mation to two-dimensional flow, Betz’s apparatus gave him two sets of data: (1) direct measurements of lift and drag and (2i) pressure measurements dis­tributed over the surface of the wing.

The direct measurements of lift and drag showed the familiar pattern, which partially conformed to, and partially violated, theoretical expectations. The observed lift increased in the predicted, linear fashion with angle of in­cidence, but only from about -9° up to about +10°, at which point the wing stalled. Even over this range the predicted lift was significantly higher than the observed lift. In fact, the observed lift was only about 75 percent of the predicted value. And, of course, there was an observed drag when, theoreti­cally, it should have been zero. There was also another general feature of the flow that Betz observed. Theoretically each angle of incidence should cor­respond to one, and only one, value of the lift. Betz found that if he took a sequence of readings in which the angle of incidence was increased in a stepwise fashion, and another sequence in which it was decreased, a given angle might correspond to one value of the lift in one sequence and another value in the other. There were two values of the lift corresponding to each of these angles, not one. This effect was particularly noticeable above the stalling angle. Thus, at +15°, the coefficient of lift had the values of 0.68 and 0.55. Such a phenomenon fell wholly outside the scope of the theory.

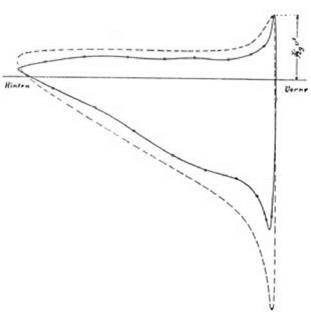
The most important results, however, were those relating to the distri­bution of pressure. Here Betz’s graphs of the manometer readings showed a definite similarity to the theoretical graphs prepared by Blumenthal and his colleagues at Aachen. Betz’s results are shown in figure 6.11. Note that

figure 6.ii. Betzs pressure graphs for a Joukowsky aerofoil at 6°. Theoretical predictions are indicated by the broken line and experimental results by the solid line. There is a similarity between prediction and observation, but Betz wanted to improve the fit. From Betz 1915, 176. (By permission of Oldenbourg Wis – senschaftsverlag GmbH Munchen)

Betz used a convention different than Blumenthal’s when drawing his dia­grams, and the data for the upper side of the wing are now placed below the base line. Significantly, the general shape of the graph derived from theory and that of the graph derived from experiment were the same. Betz, how­ever, pressed the comparison into greater detail. He was interested in getting information about the residual deviations between theory and reality, “die Abweichungen der Theorie von der Wirklichkeit” (173). This was the stated purpose of the experiment. He therefore drew attention to where the empiri­cal distribution differed from the theoretical distribution. The areas under the empirical graphs were clearly not the same as those under the theoretical graphs. These areas were proportional to the lift, and the theoretical area was significantly greater than the observed area. This was consistent with the fact, mentioned earlier, that the directly measured lift was less than the theoreti­cally predicted lift. What was the cause of the difference, and what should be done in response to it?

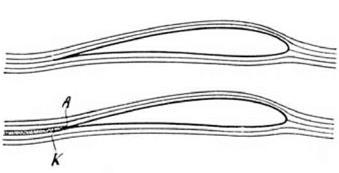
Like Fuhrmann, Betz located the source of the difference between the the­oretical and empirical flow in the tail region. Theoretically, if the Kutta condi­tion is satisfied and the wing profile is that of a pure Joukowsky contour, and if the air acts like an ideal fluid, then the flow along the upper surface will meet the flow along the lower surface in a smooth way at the trailing edge. In reality, however, the air did not behave in this way at the trailing edge, so Betz made a conjecture. It was a characteristically Gottingen conjecture (see fig. 6.12).

Betz suggested that, although the flow of air along the lower surface runs smoothly along the common tangent, the flow along the upper surface does not. Rather, it detaches from the upper surface before reaching the trailing edge, and this leaves a gap between the two flows. The intervening space be­tween the flows, said Betz, constitutes a turbulent wake filled with “Karman vortices” (177).

Betz argued that the effect of this separation is twofold. First, it disrupts the pressure relations in the vicinity of the trailing edge and disturbs the equi­librium between the forward-pointing and backward-pointing components of the pressure distribution. Since it is this equilibrium that generates the zero drag of an (ideally) efficient aerofoil, the disturbance must be a contributory cause of the observed drag. Second, the vortices in the wake draw off energy, and this has the effect of lowering the circulation around the aerofoil and hence diminishes the lift. Betz conceded that it was difficult to analyze these processes rigorously but suggested a simple (and intriguing) way to model the situation using the resources of inviscid theory. He proposed rejecting the Kutta condition and relocating the stagnation point. Whereas Kutta had used the position of the stagnation point to fix the amount of circulation, Betz reversed the process. He used the amount of circulation to fix the stag­nation point.

Betz began with the value for the lift at a given angle of attack that he had found in his experiment. He then inserted the value into the basic Kutta-

figure 6.12. Wake formation near trailing edge was cited to explain the difference between predicted and observed results. To correct for this error in prediction, Betz abandoned the Kutta condition that the rear stagnation point should be at the trailing edge. From Betz 1915, 177. (By permission of Oldenbourg Wissenschaftsverlag GmbH Munchen)

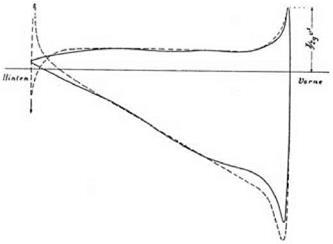
Joukowsky theorem L = p V Г. Because he knew the density and velocity of air in the wind tunnel, the formula allowed him to deduce the value of the circulation. He then used this empirical value of the circulation to tell him where the rear stagnation point must be relocated according to the theory of inviscid flow. (Betz was working with a Joukowsky profile, so this point could be calculated by transforming the flow around a circular cylinder.) Given that the empirical value of the circulation is lower than the theoretical value, the stagnation point is on the top surface of the aerofoil, rather than precisely at the trailing edge. It was then possible to replot the theoretical speed and pres­sure distributions and compare them afresh with the empirical curves. The question was whether the revised location of the stagnation point brought the empirical and theoretical graphs onto closer accord. The method automati­cally equalizes the areas under the empirical and theoretical curves but the question remains: do the distributions agree? Betz’s revised graph, superim­posed on the empirical curve, is shown in figure 6.13. The improvement is clear. The graphs are now almost identical. Betz pronounced the agreement to be “extraordinarily good.” As he put it,

Sehen wir von der nachsten Umgebung der Hinterkante ab, fur die ja Voraus – setzungen der theoretischen Stroming vollstandig andere sind wie in Wirk – lichkeit, so mussen wir die Ubereinstimmung der beiden Kurven aufieror – dentlich gut bezeichnen. (177)

If we disregard the vicinity of the rear edge, where indeed the presuppositions of the theoretical flow wholly differ from reality, then we would have to char­acterize the agreement of the two curves as extraordinarily good.

Betz had thus brought theory and experiment into closer accord. His proce­dure involved interweaving them in an interesting way, and the methodologi­cal principles implicit in the process are worth looking at with some care.

The Kutta condition had become established as one of the central as­sumptions of the circulation theory. Could Betz really afford to modify its role in this way? The overriding advantage of the Kutta condition was that it avoided the need for the ideal fluid to move around the trailing edge at an in­finite, and physically impossible, speed. How did Betz justify the reintroduc­tion of infinite speeds given that the need to avoid them was routinely cited whenever the Kutta condition was invoked? The point was addressed explic­itly in the paper. The argument was as follows: Since perfect fluid theory is known to be unrealistic from the outset, said Betz, one more piece of unreal­ity hardly matters. The entire approach is an artifice, so this should not be disturbing. The infinite speeds are just the way that the complicated, physical

figure 6.13. Betzs revised pressure graphs after modification of the Kutta condition. The observed and predicted curves are now closer. From Betz 1915, 178. (By permission of Oldenbourg Wissenschafts – verlag GmbH Munchen)

processes at the trailing edge receive some manner of recognition within the terms of the theory. Their presence in the analysis simply indicates that fur­ther assumptions need to be introduced to mediate between reality and the idealized picture. Outside the wake, the flow can be reasonably modeled by ideal-fluid theory, and the presence of the wake can be taken into account by lowering the value of the circulation. This approach can be seen as the first step toward a better account of the phenomenon. As Betz put it,

Dafi dabei ein Umstromen der scharfen Hinterkante stattfinden mufite, was praktisch unmoglich ist, braucht uns nicht zu storen, da ja die Stromungen. . . bis zu dem gemeinsamen Ablosungspunkt nur ein theoretischer Ersatz sind fur die in Wirklichkeit vorhandenene Wirbelbewegung. (177)

That this would have to result in a physically impossible flow round the sharp trailing edge need not disturb us. This is because the flow. . . up to the com­mon point of separation is only a theoretical substitute for the vortex motions that exist in reality.

The assumptions behind this talk of a “theoretical substitute” (“theoretischer Ersatz”) can be clarified by noting what Betz had said about d’Alembert’s paradox. Notoriously, the theory developed by Kutta and Joukowsky pre­dicted that a wing will have zero resistance. Betz, however, defended the use of an inviscid theory as an approximation, “even though it does not permit any statements to be made about the resistance” (“trotzdem sie uber den Widerstand nichts auszusagen vermag”; 173). What did Betz mean by this? Surely, the theory does permit a statement to be made about resistance. In­deed, it requires that a statement should be made: namely, the false statement that the resistance is zero. Betz knew this, so what he must have meant was that the theory does not permit any useful statement to be made. The theory doesn’t shed any light on the resistance. His question was: To what practical purpose can the theory be put? The theory was being viewed as a tool rather than a body of propositions. Perfect fluid theory is a useful tool for certain purposes but not for others. Betz was telling his readers that questions about the utility of the theory, rather than its literal truth, should be uppermost in their minds. That is why they should not be unduly disturbed by theoretical deductions that entail infinite speeds.