Anyone for Tennis?

Lanchester offered no quantitative expression for the dependence of lift on circulation. He presented many of his main results in a verbal or pictorial form. A modern textbook of aerodynamics would give a mathematical for­mula to express the central ideas of Lanchester’s theory of lift. The formula would be

Lift = рГУ,

where p is the density of the air, Г is circulation (that is, the value of the integral described earlier), and V is the speed of the wing relative to the un­disturbed air.

It is a matter of some historical interest that this important formula had been published in 1877 by Lord Rayleigh. Rayleigh did not, however, offer it as a law that might govern the lift on an aircraft wing. He reserved that role for the very different formula he had published in the previous year describ­ing the pressure on a flat plate created by a discontinuous flow. How and why did Rayleigh arrive at the рГУ formula? I want to look into this matter and then come back to Lanchester.

The short paper in which the formula appeared was titled “On the Ir­regular Flight of a Tennis Ball.”15 In it Rayleigh posed the question of why a spinning ball sometimes veers to one side in flight: “It is well known to tennis players that a rapidly rotating ball in moving through the air will often deviate considerably from the vertical plane. There is no difficulty in so projecting a ball against a vertical wall that after rebounding obliquely it shall come back in the air and strike the same wall again” (344).

In posing his question Rayleigh would have been thinking of the old game of royal or real tennis, which was played indoors and involved a net strung between two walls. In this form of tennis the players are permitted to use the walls and hence produce the effect that Rayleigh mentioned.16 Real tennis courts only existed in a few country houses and ancient universities, but there were (and still are) courts in Cambridge. It was Rayleigh’s chief recreation as an undergraduate.17 Rayleigh rejected the idea that the trajectory of the ball deviated from a straight line because the ball “rolled” on a cushion of con­densed air that had formed in front of it. That, he noted, would produce a deflection in the wrong direction. The correct answer, he said, had been given in a qualitative form by the Berlin scientist Gustav Magnus in 1852. Magnus had been interested in artillery shells rather than the more gentlemanly tennis ball.18 The present paper, said Rayleigh, was designed to supplement Magnus’ answer with a mathematical formulation.

To simplify the problem Rayleigh assumed that the ball was stationary and the air flowed uniformly past it. If the ball is not spinning, all the forces, frictional and otherwise, will be in the direction of the air stream. To produce a deviation in the trajectory there must be a lateral force. This force depends on the rotation of the ball, which, by friction between the ball and the air, produces what Rayleigh called “a sort of whirlpool of rotating air” (344). If the whirlpool is combined with the uniform stream, the velocities oppose one another on one side of the ball and augment one another on the other side. This velocity difference produces a pressure difference and hence a side force. This time the force is in the correct direction. “The only weak place in the argument,” said Rayleigh, “is in the last step, in which it is assumed that the pressure is greatest on the side where the velocity is least. The law that a diminished pressure accompanies an increased velocity is only generally true on the assumption that the fluid is frictionless and unacted upon by external forces; whereas, in the present case, friction is the immediate cause of the whirlpool motion” (345). The law relating diminished pressure with increased velocity was Bernoulli’s law, and Rayleigh was rightly sensitive to
the preconditions of its legitimate use. Despite the questionable character of this step in the argument Rayleigh continued to develop the analysis in terms of a circular cylinder “round which a perfect fluid circulates without molecu­lar rotation.” What was meant by “molecular” here? Rayleigh was explicitly working with an ideal or perfect fluid, so the “molecules” would actually be fluid elements. Rayleigh would not have been confusing them with the mol­ecules of the chemist. He was simply postulating an irrotational flow of an incompressible, inviscid fluid with circulation.

Rayleigh proceeded to write down the stream function for the flow he was postulating. He was able to do this by adding together the stream functions for the two components of the flow, namely, the stream functions for a uni­form flow round a cylinder and for a vortex round a point. The formula he used was, in his notation,

r sine + ySlogr,

where r and 0 are the polar coordinates of any point in the fluid and a is the radius of the cylinder. The two symbols a and в are constants proportional to the velocity of the free stream and the circulation, respectively. Examina­tion of Rayleigh’s formula shows that it can be related to the examples I have discussed in previous sections. The first part is the stream function that was discussed in chapter 2 for the flow around a circular cylinder. The second part, involving the log term, was introduced earlier in this chapter as the stream function of a vortex.

Rayleigh used this formula to arrive at an expression for the velocity and hence the pressure at any point on the surface of the cylinder. The lateral component was integrated around the circular cylinder to give the resultant lateral force. The expression that Rayleigh arrived at was

2n

I (P – P0 )a sinede = -2mxp,

0

where p is the pressure at the surface of the cylinder and p0 is the pressure at infinity. The other symbols have the meanings already assigned. The conclu­sion indicated by the final term of this equation was that the lateral force causing the irregular flight of the tennis ball was “proportional both to the velocity of the motion of circulation, and also to the velocity with which the cylinder moves” (346). This is essentially the result on which Lanchester’s analysis depended, and the right-hand side of the above equation is equiva­
lent to the law relating lift to density, circulation, and velocity. The minus sign on the right-hand side of the above equation indicates direction, the circulation is Г = 2пв, while the free-stream velocity is V = a. Rayleigh took the density of the air to be of unit value, which explains why the term p did not appear in his final formula.

Having arrived at the lateral force on the tennis ball, Rayleigh asserted without argument (but citing the authority of Kelvin) that, under the sim­plified conditions of the example, the trajectory of the tennis ball would be along the arc of a circle, the motion having the same direction as the circula­tion.19 Rayleigh’s analysis was taken up and extended by Greenhill in a paper published in 1880 in which the equation of the trajectory was deduced in an explicit way.20 Further, whereas Rayleigh had ignored external forces such as gravity, Greenhill reintroduced this complication and showed that its effect was to give the trajectory the form not of a circle but of a trochoid.21

How seriously did Rayleigh take his analysis of the tennis ball and, by implication, the artillery shell? His aim in the paper, he explained, had been to “solve a problem which has sufficient relation to practice to be of interest, while its mathematical conditions are simple enough to allow of an exact so­lution” (345). These words reveal the element of judgment that entered into the exercise. Relevance was being traded with simplicity. A balance was being struck, but Rayleigh evinced some doubts about the terms of the exchange. His final words in the paper referred back to what he had called the weak links in the argument. The behavior of a real fluid would give rise to a wake behind the ball, and this aspect of the flow finds no recognition in the analysis. Ray­leigh thus ended his paper with a warning: “It must not be forgotten that the motion of an actual fluid would differ materially from that supposed in the preceding calculation in consequence of the unwillingness of stream-lines to close in at the stern of an obstacle, but this circumstance would have more bearing on the force in the direction of motion than on the lateral compo­nent” (346). The informed reader of Rayleigh’s paper would know that there was a mathematical approach that could represent this “unwillingness” of the streamlines to close in behind an obstacle. Such an analysis was provided by the theory of discontinuous flow and free streamlines. Perhaps this would do more justice to the complex reality of the case. Explicitly, then, the reader was given a circulation analysis but, implicitly, was being directed toward the theory of discontinuous flows.22

Lanchester also had an account of the swerving tennis ball in his book on aerodynamics. His account did not invoke the circulation theory but ap­pealed to the discontinuity theory, that is, to the picture of Kirchhoff-Rayleigh

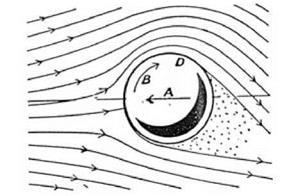
figure 4.9. Lanchester’s account of why a spinning ball generates lift. Notice the presence of the dead air behind the ball and hence the appeal to the discontinuity theory. From Lanchester 1907, 43.

flow. Lanchester’s discussion of the spinning ball was given in a section of his book titled “Examples Illustrating Effects of Discontinuous Motion.” The diagram he used to illustrate his analysis is given here in figure 4.9. The figure shows a ball moving through a viscous fluid, such as air, where the direction of motion is shown by the arrow A, and the rotation by arrow B. In this case the ball will veer upward. Like Rayleigh, Lanchester drew attention to the in­crease in the speed of the air on one side (here the top) and its diminution on the other side (the bottom). Where Rayleigh merely hinted, Lanchester was explicit that the flow round the ball creates dead fluid behind it. He argued for this concept on experimental grounds. The effect of the spin was then said to modify the shape of the dead air, as is shown in the figure. Lanchester claimed that at the top of the dead-air region, the spin helps to expel the dead air. At the bottom, the spin helps to draw in the dead air and spread it along the lower surface of the ball. This action was said to have the effect of giving the ball an upward thrust.

In retrospect, familiarity with the circulation theory of lift makes it easy to assimilate the case of the spinning tennis ball and the case of the wing and to see the possibilities inherent in treating both of them as involving circulation. It is evident that for Rayleigh and Lanchester the situation was not clear cut and both inclined toward an eclectic account. In broad terms it can be said that Rayleigh used the discontinuity theory to explain wings but the circula­tion theory to explain tennis balls. Lanchester did the opposite and used dis­continuity theory to explain the swerve of tennis balls and circulation theory to explain the lift of wings.

Professor or Practical Man?

Not long after its publication, the first volume of Lanchester’s Treatise be­came the topic of a seminar discussion in Gottingen, and Lanchester was approached for permission to produce a German translation. He received a letter to that effect from Prof. Carl David Runge. At first Lanchester had no idea who Runge was, but inquiries soon revealed that he was an emi­nent applied mathematician. He had done work on methods of numerical approximation used to solve differential equations as well as having discov­ered empirical formulas to predict spectral lines.23 Runge had been brought from the technische Hochschule in Hanover to the university in Gottingen at the behest of Felix Klein. During the session of 1907-8 Runge had joined Prandtl in giving a seminar on hydro – and aeromechanics. They discussed Lanchester’s book, and Runge penned his letter to Lanchester in March 1908. In September, Lanchester visited Runge in Gottingen to discuss the transla­tion, and they became lifelong friends. Runge was impressed by Lanchester’s vigor and humor, which were very different from the demeanor of the aca­demic Englishmen he had met before. Lanchester was a guest of Runge and his wife and amused their young sons by flying model gliders. Lanchester recalled that one evening Prandtl and von Parseval (the airship designer)24 “blew in” for a beer. A convivial time was had, though communication was limited by Lanchester’s lack of German and Prandtl’s lack of English. Runge, by contrast, spoke English with a perfection that amazed Lanchester.25 The German translation of the Treatise was a collaborative effort by Runge and his wife. The first volume was published in 1909.26

Lanchester’s appointment to the Advisory Committee for Aeronautics in 1909 is not difficult to understand in general terms—though exactly how it came about remains unknown. He had published a substantial work on aero­nautics and was an engineer with a proven record of innovation. His knowl­edge of engine design was considerable, and the difficulty of producing light, powerful, and reliable engines remained a major stumbling block to progress in aviation. Lanchester grumbled retrospectively that Glazebrook thought that this was his only area of expertise: “he always treated me as if I was ap­pointed purely for my knowledge of the internal combustion engine.” In the hope of being taken seriously on a broader front, Lanchester had distributed six copies of his treatise Aerial Flight to his fellow committee members. Ray­leigh responded with an appreciative letter and gave Lanchester four volumes of his collected papers in return. Of the rest, said Lanchester, only one ac­knowledged the gift, while the others “ignored it entirely.”27 Despite these slights Lanchester worked hard, both for the main committee and for the two subcommittees on which he served: the Engine Sub-Committee and the Aerodynamics Sub-Committee. His biographer described how Lanchester would attend some forty to fifty meetings a year as well as taking on the re­sponsibility of writing a significant number of papers published as Reports and Memoranda.28

While Lanchester’s appointment to the ACA is intelligible, his position on the committee was anomalous. He was a representative of the world of practical engineering on an administrative and scientific body dominated by influential Cambridge academics. He was not the only engineer or the only nonacademic or, indeed, the only non-Cambridge man on the com­mittee, but (the military representatives aside) the others were more closely integrated into academic life. Joseph Petavel was a professor of engineering at Manchester and Horace Darwin, of the Cambridge Scientific Instrument Company, had close connections with the university. This left O’Gorman and Lanchester as the only authentic examples of what the British called “practi­cal men,” but this did not spare them from the hostility that was directed against the “theoreticians” of the Advisory Committee.

Lanchester’s treatise was published before his appointment to the hated committee, so how was it received in the aeronautical and engineering press? The first volume was reviewed in Aeronautics in February 1908. The review was unsigned but was probably written by the editor, J. H. Ledeboer. The reviewer recommended Lanchester’s book for thorough study by all those who take an interest in aeronautical problems, “since it includes a mass of valuable theory.” The aircraft designer could gain “many a hint” from the book. The reviewer did not, however, identify the cyclic theory of lift among the “mass.”29 The anonymous reviewer in the Aeronautical Journal likewise greeted Lanchester’s first volume as a valuable, but difficult, contribution to aerodynamical theory and also failed to convey to the reader the cyclic char­acter of the flow postulated in Lanchester’s book.30

The same pattern was repeated in the anonymous reviews published in the Engineer, Engineering, and the Times engineering supplement.31 Florid congratulations were offered by the reviewer, but there was a signal failure to convey the actual content of the theory of lift. The words “circulation” or “cy­clic” did not feature in any of the discussions. There were also warning signs suggesting that the reviewers might have opposed the theory had they grasped it. Thus, the reviewer in the Times spoke of “doubtful hydrodynamic analo­gies” (6), while the reviewer in the Engineer noted that “Evidently the author has a deep admiration for the work of Horace Lamb” (617) and went on to say that Lanchester “somewhat naively” described how he had added the hydro­dynamic interpretation to his original ideas in order to give it a more secure basis. The naivety, presumably, lay in Lanchester’s failure to realize that, in certain quarters, invoking Lamb would reduce rather than increase credibil­ity. The reviewer in Engineering also took issue with Lanchester’s diagrams: “The diagram given on page 145 seems to indicate that particles originally in contact with the lower surface of the plane finally reach the upper by describ­ing circular paths round the edge. The true condition of affairs is, we believe, much more nearly represented by a diagram given later in the volume—viz. on page 266” (461). The complaint is revealing. As Lanchester had explained on the page before the diagram favored by the reviewer, at that point in the discussion “the flow is of the Rayleigh-Kirchhoff type” (265). The reviewer was responding to, and endorsing, a diagram that shows a discontinuous flow—precisely the picture that Lanchester was challenging.

Most of the “practical men” who read Lanchester initially extracted from him not the idea of circulation but the neo-Newtonian idea of “sweep.” The realization that circulation played a central role in Lanchester’s thinking came later. For example, Arthur W. Judge in his eclectic Properties of Aerofoils and Aerodynamic Bodies followed Lanchester in giving an account of both circula­tion and sweep, including a reproduction of some of the diagrams showing trailing vortices.32 Judge’s book was published in 1917, rather than being an immediate reaction, so there was more time for Lanchester to have dissemi­nated his ideas.33 Nevertheless, Judge did little to integrate the circulatory theory with empirical data, despite his references to some of the Gottingen publications.34

The second volume of Lanchester’s treatise was reviewed in Aeronautics a year after the first volume, and this time the hand of the editor was sig­naled by the initials J. H. L.35 He expressed “whole-hearted admiration” for the work but soon took the discussion into the vexed domain of the relation between theory and practice. “The present work once again raises the oft – debated question of the advantages in aeronautical research of the theoretical or mathematical and practical methods” (6). In the reviewer’s opinion, “vic­tory” rested with the practical methods. Admittedly, he went on, people such as Bryan, Rayleigh, “and, we may now add, Lanchester” show the path along which research is to proceed, but the fact remained that “the most success­ful machine of all,” that of the Wright brothers, was built without the aid of mathematical formulas. This, then, was, “the main reproach we could make against Mr. Lanchester’s work: it is far too theoretical” (6).

The designer J. D. North had apparently arrived at a similar conclusion. He later recalled that he had not found Lanchester’s book as useful as the more empirical, data-rich volumes of Eiffel.36 This opinion was not universal, but clearly many people saw Lanchester in this way, that is, as a representative of an overly theoretical approach. In February 1914, Herbert Chatley wrote an article in Aeronautics designed to head off the reading of Lanchester’s book as just another example of mathematical “x-chasing.”37 Chatley acknowledged that there was controversy in the technical press about the value of applying mathematics to aeronautical problems. One dimension of the problem, he said, was generational. Older engineers had been trained practically and re­sented the attempts of younger colleagues “to dominate engineering practice with mathematical theorems.” Chatley wanted to do justice to both sides and to get the competing parties to see that the problem did not have a black or white answer. The issue, he said, was always one of degree.

Chatley illustrated his conclusion by an example: “There are three books published in England by men with big reputations dealing with the theory of aviation, viz. Lanchester’s ‘Aerial Flight,’ Bryan’s ‘Stability in Aviation,’ and Greenhill’s ‘Dynamics of Mechanical Flight.’ To those unfamiliar with math­ematics these three books are classed together and, I imagine, are regarded by the majority of practical aeronautical engineers as beyond the limits of practi­cal application” (46). It was a mistake, he said, to treat these books as three of a kind. Lanchester’s book was not obscure and was of the greatest use to designers; Bryan’s book was, indeed, mathematically much more demanding, but it was genuinely engaged with real problems; Greenhill’s book, however, was quite different. It was even more mathematically difficult than Bryan’s but “very little of it has at present any application to practical problems.” As well as making discriminations of this kind, said Chatley, both sides, the prac­tical men and the mathematicians, must recognize the weakness in their own positions. The former must give up reliance on “mechanical instinct,” while the latter must “assimilate more complex conditions” rather than “elaborate hypotheses on too simple foundations” (46).

Chatley was seeking a compromise, but this desire was wholly foreign to C. G. Grey, editor of the Aeroplane. On September 12, 1917, Grey described Lanchester as “several government officials rolled into one, and a mathemati­cian, and an advisory expert, and several other equally exalted things at the same time.”38 Grey took pleasure in baiting Lanchester, who held no academic post, by calling him “Professor.”39 While granting that Lanchester’s books had their “lucid moments,” Grey claimed that, overall, they were “utterly ununderstandable. . . to the ordinary man, and even to some trained math­ematicians.” He called on Lanchester to mend his ways: “No! Mr. Lanchester. Forget your professorship for a while. Be a practical engineer” (158). In an article headed “On a Professor,” Grey described Lanchester’s main publica­tions in unflattering terms: “He has written two ponderous tomes, entitled ‘Aerodynamics’ and ‘Aerodonetics’ respectively, which profess to be math­ematical expositions of the theory of flying. On these volumes his reputation in aeronautics was founded. Not being a mathematician myself I can only ac­cept the statement of others better informed, who say that these expositions are not mathematics in the accepted sense of the term, but some science of symbols invented by Professor Lanchester.”40

What had called forth this invective? The answer is that Lanchester had ventured into what an editorial in Flight had called “the cesspool of politics.”41 He had been goaded into responding to articles that Grey had published in the Sunday Times and the Observer on July 29, 1917. Lanchester’s reply was called “A Campaign of Slander.” It appeared on August 15, 1917, in the short­lived journal Flying.42 He said Grey was indulging in “a venomous and un­restrained attack on the Air Board and upon the two branches of the Air Service.”43 These attacks repeated earlier accusations made by Pemberton Billing and Joynson-Hicks in Parliament—accusations, said Lanchester, that had been thoroughly investigated and found to be groundless. Lanchester was referring to the “murder” charge leveled at the government and to the Bailhache inquiry whose final report had been published on November 17, 1916. “No documents,” said Lanchester, “could constitute a worse indictment of the self-appointed critics, or a greater vindication of the ability, character and honour of those attacked, unless possibly that document be the record of the proceedings themselves. . . . It is probable that in our time no public enquiry has been called upon to investigate charges so recklessly made and based on so slender a foundation” (51).

Now, a year later, Grey was repeating the old complaints. Notice, said Lanchester, how those making the attacks were always “wily enough to avoid putting them in a form which would permit of their being challenged in the Courts” (51). They always expressed themselves in a vague and general way. They talked of “appalling waste,” “official designers,” a “little clique,” etc. It was a case, said Lanchester, of simply throwing mud in the hope that some­thing would stick. The ground of the attack, as before, was the allegation of official incompetence and favoritism. Even the old BE type, an aircraft cur­rently being replaced, was still under attack. “Its present survival in active service,” said Lanchester, “is talked about as an offence attributable to some interested and evil-disposed persons in authority. The whole tenor of these long abusive articles is based upon the existence of machines, any machines whatever, of official design, when (it is alleged) far better machines of propri­etary design are available” (51).

This was the nerve of the issue: the existence of official designs. The ques­tion with which we are faced, said Lanchester, “is why and to whom is the said design an offence?” (52). Had these machines failed to perform their re­quired duties? Were there any better designs available when the BE2C was put into manufacture? The answer to both questions, said Lanchester, “is clearly in the negative” (52). The BE type had been the backbone of the reconnais­sance service for three years of war. It had to bear the blame for its shortcom­ings as a fighter and for being not quite the equal in speed and climb to the Fokker, but, insisted Lanchester, it had acquitted itself “in a manner which is little short of astonishing” (52).

Lanchester then addressed Grey’s complaints about engine shortages and the mobilization of manufacturing capacity in order to improve aircraft sup­ply. In Lanchester’s opinion, none of Grey’s dramatic remedies could stand up to scrutiny. Grey had no understanding of real conditions, and his ideas about economics were naive. Grey was responding to an inevitable feature of large-scale production but was treating it as if it were a defect that could be swept away. Thus, said Lanchester,

He condemns offhand everything which is not the best. If a new machine is produced to-day which is better in its performance. . . on trial than some­thing in service, then the latter is at once condemned, and the people who tolerate its use are obvious fools or incompetent rogues! It is spoken of as murder still to employ the B. E.2c for reconnaissance, or an 80-h. p. scout as a fighter. Mr. Grey has evidently had no experience of quantity production, otherwise he would know that it is always the case, so long as there is progress, that the latest and the best designs will not be available in sufficient quantity. It cannot in the nature of things be otherwise. (53)

Grey may have been the mouthpiece of the aircraft manufacturers, but in Lanchester’s opinion he betrayed no understanding of the system of manu­facture and development.

Lanchester returned to these themes later in 1917, in the December issue of Flying. The title of Lanchester’s article was “The Foundation Stones,”44 and he set out to explain the scientific and research basis on which airplane de­sign depended. The airplane as we know it today, argued Lanchester, doesn’t merely depend on the experience of the draughtsman, the intuition of the designer, or the cunning of the craftsman but “is the ultimate outcome of scientific research” (354). Theory, both mathematical and otherwise, played a role, while engineering and physical research, carried out in the workshop, the laboratory, and with full-scale aircraft, consolidated the results already explored theoretically. Lanchester’s aim, however, was not simply to draw attention to the diversity of the scientific foundations of aeronautics. The different contributions had to be properly coordinated: “In order to secure continued progress it is vitally necessary that forces of many different kinds should act in concert, and nothing but evil can result from the worker in any particular field trying to encroach on other fields” (354). Lanchester listed the various contributors and delimited the proper scope of their activities. The mathematician may be useful but is “utterly incompetent” when it comes to “specifying or designing an aeroplane” (345). The mathematician’s field is im­portant but narrow. Unfortunately, many mathematicians are men of “child­like simplicity” and fail to understand that there is anything beyond their symbols. Physicists also have a vital role but “only one degree less narrow” than that of the mathematician. “For the physicist to invade territory outside his own ken would certainly not lead to satisfactory results” (354). The engi­neer is responsible for design and construction. “His job is frequently that of a buffer.” He has to listen to both the mathematician and the physicist but he must also be responsive to the requirements of the user, and pay attention to economic considerations and, in times of war, to shortages of materials and the problems of substituting one material for another. The pilot also had a legitimate claim to be heard, as did the military and naval authorities who ordered the aircraft and were responsible for its deployment.

Lanchester had no illusions about a system of this kind. As a realist he knew there would always be clashes of interest. They were inevitable and could not be wished away, but they were not always bad in their effect. In a tilt at the press campaigns he declared: “Now there are many who think that fric­tion in the management of our Air Services as between one department and another, or between different departments and manufacturers, or between the military authorities at the Front and those at home, etc., is essentially a sign of bad management and muddle. No such idea is justified” (354).

Theoretically, if a single “autocrat” were in control, friction might be avoided, but even then the autocrat would have to defer to those with spe­cialized knowledge. In reality the answer lay in the proper division of labor and clear, long-term policies. “The greater part of the difficulties that have arisen in the past have been due to two causes, one a failure to define prop­erly the spheres or fields of activity of the different contributory factors; the other an absence of foresight and far-sighted policy, both in detail and in the gross” (354).

As an example of a failure of foresight, Lanchester pointed to the attacks on mathematicians and physicists and their condemnation as impractical. At times these specialists may have made themselves too prominent, but their contributions are indispensable. The best way to achieve the desired har­mony between the different factions “can only come from each man putting up as stout a case as he can for his particular views,” while being prepared to listen to the views of others. Such negotiations have something of the char­acter of a game of chess. We should not forget that when a mistake is made, its consequences “may often be so remote as to defy immediate analysis,” or that the winning move “may have every appearance at the time it is made of being a blunder” (355).

In Lanchester’s opinion, “indiscriminate Press criticism and stump ora­tory” only served to distract from the serious business of the war (355). Jour­nalists who thought they were omniscient, he went on, merely traded on the ignorance of their fellows. The proper way to proceed was shown by the late E. T. Busk, who acted as a “bridge between the scientific man, the engineer and the pilot” (356). In the period leading up to the war, opinion was divided on the value of the inherent stability of an aircraft. Physicists and mathema­ticians, said Lanchester, strongly supported stability, while many pilots had been against it (as had the Wright brothers). The military authorities didn’t know what to do. Busk resolved this dispute and “proved the value of in­herent stability” (356). Lanchester accepted that since Busk’s work, in 1914, knowledge of how to balance the relative virtues of stability and instability had been deepened. Despite these subsequent advances, the “BE2C machine was the immediate outcome of his work, and it is worthy of note that every Zeppelin brought down in night flying in this country was brought down by a machine of this type. For a long time it was the only machine which could safely be sent up or flown in the dark. Beyond this, for the first twelve months of the war, and more (up to the spring of 1916), nearly two thirds of the total enemy aeroplanes brought down on the Flanders front were brought down by the BE2C” (356).

Lanchester was the only member of the Advisory Committee for Aero­nautics to engage in public with the likes of Grey and Pemberton Billing. He was appalled at their activities and had the civic courage to say so. He was also disturbed by the mounting evidence that Billing was conducting his campaign with the help of inside information provided by a member of the Advisory Committee itself. That member, Lanchester concluded, was the naval rep­resentative Murray Seuter. Lanchester complained in letters to A. J. Balfour and G. A. Steel at the Admiralty that Seuter was a slacker who did not pull his weight and abused his position of trust. Lanchester’s suspicions had been aroused when he had shown Seuter an article he intended to publish in one journal but had then decided to publish elsewhere. Within an hour of showing the document to Seuter, one of Billing’s supporters had rung up the original (that is, the wrong) publisher to raise objections. “I think,” said Lanchester pointedly, “Commodore Seuter should be given a change of air.”45

Although some practical men treated Lanchester as if he were a mere theoretician, in his own understanding he was very much the engineer. He had a sharp sense of the proper relationship of the engineer to the mathema­tician and physicist and of the differences in their perspective. I shall now look at how this sense of difference was reciprocated by mathematicians and physicists themselves. I review, in roughly chronological order, a sequence of critical responses to the circulatory theory of lift, as they were advanced by the high-status, mathematically sophisticated British experts in aerodynam­ics, and I identify all of the main objections. Running against the flow of these objections were some experimental results that might have worked in Lanchester’s favor, but, strangely, these had little impact. Why this was so is part of the problem to be addressed.