Rayleigh’s Paper of 1876

In 1876 Rayleigh had published a paper called “On the Resistance of Fluids.”1 It contained one of the most striking results of classical hydrodynamics, which came to be reproduced in all the advanced treatises on the subject. By using conformal transformations Rayleigh had arrived at a formula for the

force exerted on an inclined, flat plate subject to a uniform flow of an ideal fluid (see fig. 3.1). The plate is at an angle a to a horizontal flow, and the fluid has a density p and a speed V. If the length from the leading to the trailing edge of the plate is l, then the resultant force R was

4 + n sin a

The resultant is perpendicular to the plate, that is, inclined backward at an angle a so that the vertical (lift) component would be R cosa and the hori­zontal (drag) component would be R sina. Rayleigh was also able to work out the position of the center of pressure, that is, the precise distance of the resul­tant force from the leading edge of the plate. The analysis was carried out in two dimensions, that is, the plate was assumed to be very long. The diagram thus represents a cross section in the middle of the plate, and what happens at the ends of the plate is ignored. The dead fluid can be seen to form a “wake” stretching downstream to an indefinite extent.

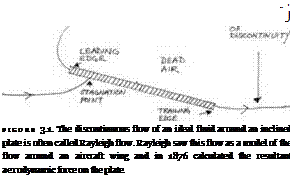At the time of its publication Rayleigh had presciently remarked that his result had interest because “it will be of vital importance in the problem of artificial flight” (431). The diagram in figure 3.1 is thus a drawing of a wing. Nearly thirty years before the success of the Wright brothers, Rayleigh had been attuned to the problem of explaining the lift of an aircraft wing and had offered a theoretical analysis, and perhaps even a solution, to the problem of how it generates lift. Rayleigh had the reputation, as a physicist, of being somewhat conservative.2 His forward-looking orientation to the problem of explaining lift is therefore all the more noteworthy, given that contemporaries such as Lord Kelvin were declaring that they had “not the smallest molecule

of faith in aerial navigation.”3 In 1909 the task the Advisory Committee set it­self was to see if, and how, Rayleigh’s early approach could be carried further. Greenhill, the mathematician on the committee, and himself an authority on hydrodynamics, set about consolidating and extending Rayleigh’s mathemat­ical analysis. Mallock and his collaborators, meanwhile, surveyed the work of other laboratories and used the resources of the NPL to gather relevant empirical data.

When Rayleigh (see fig. 3.2) first published his formula, there was little experimental data available on air or water resistance against which it could be tested. He had to rely on some old experiments made with an unsatisfac­tory type of apparatus called a whirling arm, which consisted of a horizontal beam or arm that rotated around a vertical axis. The arm had the test object at one end and a means (such as a spring) for measuring the force on it. The problem with an apparatus of this kind was that the test object was repeatedly exposed to the turbulence caused by its previous orbits. These experiments had, however, shown that resistance depended on the sine of the angle of incidence, and this result accorded with Rayleigh’s formula.

The first impression, in 1876, was that theory and experiment agreed

“remarkably well” (437). The impression did not last. By 1891, when Rayleigh reviewed Langley’s Experiments with Aeronautics for Nature, he knew that the experimentally determined relation between the angle of incidence and the aerodynamic force on a flat plate diverged from that stated in his formula.4 If the results are expressed as a graph and the lift force on the plate is plotted against angle of incidence, the curve that derives from Rayleigh’s theory is strikingly different from that derived from experimental measurements of these quantities.5

Rayleigh had a good idea where the trouble lay. It was a matter of what happened on the rear face of the plate. He cited experiments in which the pressure on the back of a plate had been measured. This was done by us­ing a hollow plate and making a hole in the rear surface. A thin pipe was led from the hole through the hollow plate and connected to a manometer. These measurements showed the presence of a suction effect. Rather than the assumed atmospheric pressure, there was a lowering of pressure, which was inconsistent with the model. As Rayleigh conceded, “It will naturally be asked whether any explanation can be offered of the divergence. . . from the theo­retical curve. . . . It seems probable that the cause lies in the suction operative, as a result of friction, at the back of the lamina. That the suction is a reality may be proved without much difficulty by using a hollow lamina. . . whose interior is connected with a manometer” (495). Rayleigh’s 1876 analysis, of course, was based on ideal fluid theory, and therefore the results of friction and viscosity had been ignored.6

Rayleigh had also ignored all the eddies in the flow that would be expected on the basis of simply observing, say, the flow of water past a barrier. Lord Kelvin (Sir William Thomson) objected in the pages of Nature that the “dead water” behind a barrier, or the “dead air” on the upper surface of the wing, was far from dead: it was full of turbulence and instability.7 But if the dead fluid wasn’t really dead, then the free streamlines would be unstable and the entire picture of the flow would be compromised. Rayleigh did not deny that there was a problem here but initially sought to play down its significance. Thus, “it was observed by Sir William Thomson at Glasgow, that motions involving a surface of separation are unstable. . . . But it may be doubted whether the calculations of resistance are materially affected by this circum­stance, as the pressures experienced must be nearly independent of what hap­pens at some distance in the rear of the obstacle, where the instability would first begin to manifest itself” (437). And there the matter was left.

In the analysis of the lift and drag of a wing, the situation was therefore very different from that which prevailed in the study of stability. The pro­gram of research begun in 1909 by the Advisory Committee was, from the outset, plagued with doubts and anomalies. Quantitatively, the predicted lift and drag were not accurately rendered by Rayleigh’s model, and qualitatively they did not seem to correspond to what was known about the physical fea­tures of the flow. Undeterred, the committee pressed on with their program of research.