The Indirect Method and Complex Variables

After introducing Laplace’s equation, Cowley and Levy made the following observations about its centrality to the mathematics of ideal-fluid flow: “The real key to the solution of any problem in the irrotational motion of a non­viscous fluid lies in the determination of the appropriate expression that sat­isfies this equation and at the same time gives the requisite boundaries to the fluid” (44). If this is the “real key,” then where and how is the key to be found? I have just indicated that some flows can be built up by combining the
stream functions of existing flows, but how does the process get started? How were these stream functions arrived at? Apart from the simplest possible of all flows, the primordial straight-line, steady flow, how does the mathema­tician determine which expressions satisfy Laplace’s equation and meet the requisite boundary conditions? Cowley and Levy acknowledge that it is not easy and draw attention to the expedients that have been used to cope with the difficulty.

One expedient is called the indirect method. Instead of beginning by stating a problem (for example, what is the mathematical description of the flow around such-and-such a given object?) the researcher starts with some known piece of mathematics and asks what flow it might be used to describe. Various mathematical functions are investigated to determine which bound­aries might be fitted to them. The difference between the direct and indirect approach is like that between the carpenter who wants to put up a shelf and looks for a suitable piece of wood, and the carpenter who finds an interesting piece of wood lying around and looks for an opportunity to use it. As Cowley and Levy put it, “it will be clear that this indirect method of attack does not furnish a method of obtaining the solution of any proposed problem but rather furnishes the solution from which the problem is obtained” (51-52). This method works because there is a rich field of possible candidates. There is (so to speak) a lot of interesting wood lying around. In this and the next section, I show why there are so many solutions in search of problems. I then look at some more direct lines of attack on the problem of arriving at a mathematical description of a desired flow. The survey will reveal what is, at first sight, an almost uncanny relationship between pure mathematics and the physical world. This feature is one of the most intriguing in classical hydrodynamics.

A body of mathematics called the theory of functions of a complex vari­able places a large body of material at the disposal of the student of hydrody­namics. Complex variables are really just pairs of numbers which represent the coordinates (x, y) of a point relative to a standard coordinate system. But instead of a number pair (x, y), the coordinates are expressed in the form z = x + iy, where i = V – 1. Conventionally the symbol x is called the “real” part of the complex number z, and y is called the “imaginary” part. The symbol i is sometimes called an imaginary number.29 Complex numbers obey all the usual rules for manipulating numbers apart from needing the extra rule that і2 = -1. A function of a complex variable is some combination of complex numbers z whose value is arrived at by adding or multiplying the variable z or subjecting it to some other mathematical operation. Thus, to take an example that will play a prominent role in the story, f(z) = z + 1/z is a function of a
complex variable. Insert a value of z into the formula, perform the requisite operations (finding the reciprocal and adding), and out comes the value of the function f(z). Classical hydrodynamics was able to develop as it did be­cause of the fortunate and remarkable fact that every function of a complex variable w = f(z) turns out to represent a possible two-dimensional flow pattern of an ideal fluid in irrotational motion. There are an infinite number of such functions, some simple, some complicated, but they all represent a possible flow of an ideal fluid.30

I illustrate this remarkable fact by a particular case. It is a case used by Cowley and Levy to illustrate the inverse method, that is, to show how one can, for whatever reason, begin by looking at a piece of mathematics dealing with complex variables and then realize its significance as a description of a possible flow. The example also shows how every function of a complex vari­able embodies the formula for both the potential lines and the streamlines of a possible flow. The potential function ф occurs as the real part of the complex function, while the stream function у occurs as the imaginary part. The link between the two sets of lines, the streamlines and the lines of equal potential, can be represented by writing f(z) = ф + iy.

Cowley and Levy invite their readers to “consider” the function f(z) = (z + l/z). What is the flow that could be represented by this function? This flow can be found by explicitly writing out the function in terms of the more familiar x and y notation. Recalling that z = x + iy and that i2 = —1, then sub­stitution in the formula for f(z) gives

Ф + iy = z + — = (x + iy) +– .

z (x + iy)

The numerator and denominator of the last term are multiplied by (x — iy), and then all the terms on the right-hand side can be put over the same de­nominator (x2 + y2). Rearranging and grouping together the real and imagi­nary parts of the expression gives

. . . x — iy x(x2 + y2 +1) ,y(x2 + y2 — 1)

(x + iy) +— — = —————- – + i————– 2.

4 ” 2.2 2.2 2.2

Examination of the right-hand side of the above equation will reveal that it has the formf(z) = ф + iy. It is now easy to read off the formulas for the po­tential lines and the streamlines of a possible flow.

The potential lines ф= c are given by the real part of this expression, thus

x(x2 + у2 + 1)

2 2 x + у

The streamlines, у = c, are given by the imaginary part of this expression, thus

y(x2 + y2 -1) у = —

T 2,2

x + y

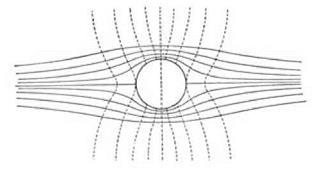
The family of curves у = constant gives the equations of the streamlines, and one of these can be interpreted as the outline of the boundaries that constrain the flow, that is, the shape of the body around which, or along which, the fluid is flowing. Consider the streamline represented by у = 0. This equation calls for either of two conditions to be satisfied. It requires that either y = 0 or (x2 + у1 – i) = 0. The first of these conditions is satisfied if the x-axis (that is, the line y = 0) is a streamline. The other condition is fulfilled if x2 + y2 = 1. This condition is met by points that fall on the circle of radius i, whose center is at the origin. Both of these will be streamlines of the flow represented by the function /(z). In other words, the function can be understood as giving the mathematical description of a flow along the x-axis, which then goes around a circular cylinder of unit radius. If the formula had been (z + a/z) rather than (z + 1/z), the flow described would be that around a circle of radius a.

What about the velocity of the flow? Recall that the velocity components of a flow are given by differentiating the stream function. Thus

ду 2xy

~дХ = (x2 + y2)2′

To find the velocity at a great distance from the circular cylinder (which has its center at the origin) one must ask what happens when the values of x and y become very large. Because of the squared term in the denominator, the frac­tional terms in the previous equations will tend to zero. Thus “at an infinite distance,” as Cowley and Levy put it, u = -1 and v = 0. At a large distance from the cylinder, the flow has unit velocity along the x-axis (from right to left) and that is all. On the surface of the cylinder, one point that can be selected for consideration is x = 1 and y = 0, that is, the very front of the cylinder. Here substitution in the previous formulas gives u = 0 and v = 0, so this point is called a stagnation point or a stopping point of the flow. The upshot is “that the circular cylinder is stationary and the fluid is streaming past it with unit velocity at infinity” (46).

figure 2.4. Flow past a circular cylinder. The continuous lines indicate the streamlines of the continu­ous flow of an ideal fluid moving horizontally past a circular cylinder. The dotted lines indicate lines of equal potential. From Cowley and Levy 1918, 46.

This worked example illustrates the way that (given sufficient ingenuity) the mathematical behavior of a function and its geometrical representation can be read, retrospectively, as providing a picture of a flow. The diagram given by Cowley and Levy showing the flow generated by f(x) = z + l/z is reproduced here as figure 2.4. The solid lines represent the streamlines; the dotted lines represent the lines of equal potential. That the two sets of lines form orthogonal sets is evident from the figure. Inspection of the di­agram indicates two further points. First, the general rule that streamlines and lines of equal potential are at right angles breaks down at the stagna­tion points of a flow. Second, when streamlines and lines of equal po­tential are switched in their roles, it is necessary to adjust the boundary conditions.31