Bernoulli’s Equation

The Euler equations permit the deduction of an important result known as Bernoulli’s law.26 Stated simply, Bernoulli’s law implies that the pressure of the fluid increases when the velocity decreases, and vice versa. There are technical restrictions imposed on its application, but the law has many practical uses in aerodynamics. It lies at the basis of an important measuring instrument used for determining the speed of flow of a real fluid such as air. The instru­ment is called a Pitot-static probe and is used, for example, in wind tunnels to establish the speed of flow. Furthermore, every aircraft is equipped with this device in order to determine the speed of flight. The instrument registers pressures, but it yields information about velocities in virtue of the relation given by Bernoulli’s law.

Stated quantitatively, the version of Bernoulli’s law to which I have re­ferred is

p+1 pV2 = H,

where H is a constant called Bernoulli’s constant. The formula only strictly applies to the steady, irrotational motion of an ideal fluid. It refers, in the first instance, to a single streamline and relates the pressure and velocity at any point on the streamline to the value of H that characterizes the streamline. In aeronautics all the streamlines can be taken to originate from a region of constant pressure and velocity, and then all of the streamlines have the same value of H. The Bernoulli constant has the same value for all parts of the flow, and its value can be established for the entire flow if it is known for any given point in the fluid. The first term in the equation, p, is called the static pressure. The second term is called the dynamic pressure, and their sum, H, the Bernoulli constant, is the sum of the static and dynamic pressures and is therefore called the total pressure. The formula indicates that as the velocity V increases at some point in the flow, the static pressure p goes down at that point because the two quantities, p and (1/2) p V2, must always add up to the same value. Furthermore, by knowing the density p and the value of p and H, we can calculate V, the speed of the flow. This is evident because the formula can be rearranged and restated as

2(H – p)

Both the static pressure (p) and the total pressure (H ) of a flow can be mea­sured. Figure 2.3 shows a simple arrangement of tubes and manometers that

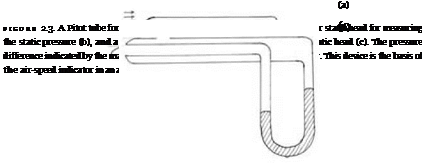would yield measures of these quantities. The total pressure measurement (a) uses an open-ended tube. The static pressure measurement (b) uses a closed tube with a small hole in its side. The side hole is called the static tap. Both tubes are connected to their respective manometers. The third part of the figure (c) indicates how the two measuring devices can be unified to form a Pitot-static probe. In the combined instrument, the single manometer mea­sures the pressure difference (H – p) needed to establish the velocity.

Measuring the speed of flow by means of a Pitot-static probe can be ac­curate to about 0.1 percent, but it has a slow response rate and demands care and suitable conditions. The formula contains a term for the density of the
air, and density varies with altitude, a fact of importance when the instru­ment is used in an aircraft to measure speed. Furthermore, the Pitot probe itself can disturb the flow it is used to measure. Small faults such as a burr around the mouth of the static tap, or a misalignment of the probe, as well as turbulence in the flow, can significantly affect the readings.27 Conditions such as the formation of ice in and around the inlet holes can also falsify the instrument readings of an aircraft, and for this reason such devices are usually equipped with electrical heating elements. The formula underlying the use of the Pitot-static probe, which I have given, only applies to airflows that can be considered as incompressible and has to be modified to allow for compression effects for high-speed subsonic flight. Yet further modifications are needed to correct for the presence of shock waves at the nose of the Pitot tube as the speed of sound is approached.28