The Euler Equations

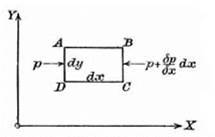
The second principle states that fluid elements obey Newton’s second law of motion, F = MX A, that is, force equals mass times acceleration. Figure 2.2 is a picture of a fluid element whose sides are parallel with the x – and y-axes. As in the previous discussion, the flow is assumed to be “two-dimensional,” so the z-axis plays no role in the analysis. The element is again assumed to be of unit depth and can be represented by a rectangle ABCD (whose “depth” bz = 1). Thus the mass of a small, rectangular fluid element with sides bx and by is pbxby. In aerodynamics the effect on the air of external forces, such as gravity, can be neglected. The resultant force on the fluid element in the x-direction comes from difference between the pressures on the two faces AD

and BC. Let the pressure on AD be p. The pressure on BC is then p+d-Sx,

dx

that is, the original pressure plus the change in pressure over the length of the element. The resultant thrust on the element is

pSy—| p+dp Sx lay=—dp Sx8y.

dx ) dx

This is the force causing the acceleration. Newton’s second law then takes the form

What is the acceleration in the x-direction? The desired term is du/dt, the rate of change of the velocity u with time t. The velocity u is a function of three variables: x, y, and t. The acceleration is given by a process of differentiation involving all three variables which is called “differentiation following the mo­tion of the fluid.”16 Thus,

du du dx + du dy + du dt dt dx dt dy dt dt dt

du dx + du dy + du dx dt dy dt dt

This expression can be simplified. If the restriction is introduced that the flow is steady, then d. = 0. Also, by definition, – А = u and – А = v. Substituting these terms in the expression for Newton’s law yields

dp I du du |

— = 4 U + V ) •

Similar reasoning gives the equation for the y-direction:

dp I dv dv

-ay=plu dX+v dy

These are the Euler equations for the two-dimensional steady flow of an ideal fluid. A mathematician will identify them as nonlinear, partial differen­tial equations that relate the pressure p and the velocity components u and v. Along with the equation of continuity they constitute the fundamental equa­tions of motion of an ideal fluid. They completely determine the motion. The integration, or solution, of the equations will, however, involve arbitrary functions and constants, and these require knowledge of (1) the initial condi­tions of the motion and (2) the position of any fixed boundaries. These two specifications are called the boundary conditions.